Densità di probabilità
Salve stavo studiando la densità di probabilità e su un sito ho letto questo esempio
Il signor Rossi aspetta una telefonata dal signor Bianchi il quale ha preannunciato che chiamerà, in un istante non meglio precisato, fra le 16:00 e le 18:00. Il signor Rossi si deve però assentare dalle 16:45 alle ore 17:00. Qual'è la probabilità che la telefonata arrivi mentre il signor Rossi è assente ?
L'istante della telefonata è una variabile casuale X. Per quanto ne sa il signor Rossi, tutti i momenti dalle 16:00 alle 18:00 sono equiprobabili, mentre fuori da questo intervallo la probabilità è zero. Dunque è intuitivo considerare X come una variabile casuale continua, la cui densità fx ha un valore costante : c sull'intervallo [16,18] ed ha il valore zero fuori di questo intervallo. Quanto vale la costante c ? Deve essere tale da soddisfare la relazione :
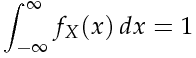
ovvero l'area del rettangolo con base [16,18] e l'altezza c sia 1. Dunque 2c=1 e perciò abbiamo c= 1/2. La funzione di densità della variabile X, sarà:
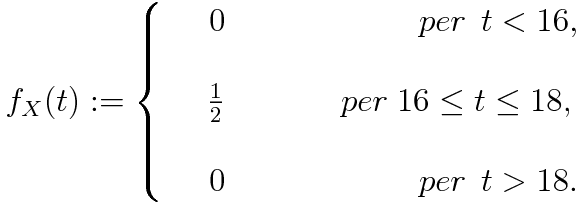
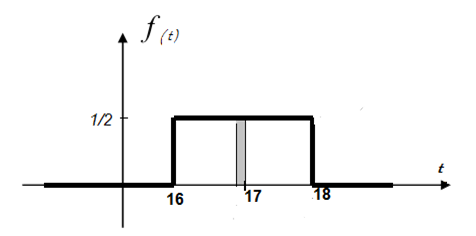
L'area grigia corrisponde alla probabilità P(16:45 ≤ X ≤ 17:00) e si nota che il valore di questa probabilità è 1/8 (l'area del rettangolo è 1)
Posso chiedervi due domande:
1) Come ha fatto a calcolare la probabilità del rettangolo (1/8)? L' area del rettangolo è ''1'' ma come ha fatto a calcolare la probabilità di 1/8 ?
2) domanda: Supponiamo che gli intervalli (a, b) (tempo nel quale si aspetta la telefonata) non siano TUTTI EQUIPROBABILI , ossia che ad esempio alle 17:58 ci sia stata una maggiore probabilità di ricevere una telefonata. In quel caso come si imposta la funzione di densità?
3) Esistono software in R per calcolare la densità di probabilità?
Il signor Rossi aspetta una telefonata dal signor Bianchi il quale ha preannunciato che chiamerà, in un istante non meglio precisato, fra le 16:00 e le 18:00. Il signor Rossi si deve però assentare dalle 16:45 alle ore 17:00. Qual'è la probabilità che la telefonata arrivi mentre il signor Rossi è assente ?
L'istante della telefonata è una variabile casuale X. Per quanto ne sa il signor Rossi, tutti i momenti dalle 16:00 alle 18:00 sono equiprobabili, mentre fuori da questo intervallo la probabilità è zero. Dunque è intuitivo considerare X come una variabile casuale continua, la cui densità fx ha un valore costante : c sull'intervallo [16,18] ed ha il valore zero fuori di questo intervallo. Quanto vale la costante c ? Deve essere tale da soddisfare la relazione :
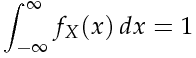
ovvero l'area del rettangolo con base [16,18] e l'altezza c sia 1. Dunque 2c=1 e perciò abbiamo c= 1/2. La funzione di densità della variabile X, sarà:
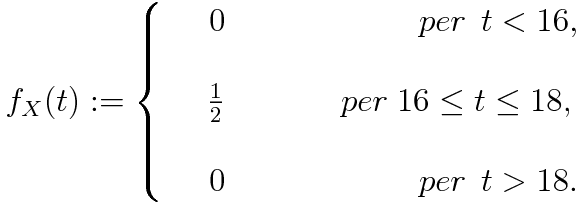

L'area grigia corrisponde alla probabilità P(16:45 ≤ X ≤ 17:00) e si nota che il valore di questa probabilità è 1/8 (l'area del rettangolo è 1)
Posso chiedervi due domande:
1) Come ha fatto a calcolare la probabilità del rettangolo (1/8)? L' area del rettangolo è ''1'' ma come ha fatto a calcolare la probabilità di 1/8 ?
2) domanda: Supponiamo che gli intervalli (a, b) (tempo nel quale si aspetta la telefonata) non siano TUTTI EQUIPROBABILI , ossia che ad esempio alle 17:58 ci sia stata una maggiore probabilità di ricevere una telefonata. In quel caso come si imposta la funzione di densità?
3) Esistono software in R per calcolare la densità di probabilità?
Risposte
"arnett":
1. Formalmente $\mathbb{P}(X\in[16.75, 17])=\int_{16.75}^{17} f_X(x)dx$ e da qui dovrebbe essere chiaro
2. Dipende, di solito una densità di probabilità è assegnata, oppure si danno informazioni più circostanziate su come determinarla
grazie.
Per ''assegnata'' intendi che si parte dall'assunto che tutti gli intervalli abbiano una determinata probabilità, precedentemente stabilita? Nulla mi vieta quindi di dire che secondo me fra le 17:45 e le 18:00 c'era una probabilità di 1/4 mentre dalle 18 alle 18:30 c'era una probabilità diversa tipo 1/3?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo