Calcolo di una probabilità di una distribuzione uniforme bivariata
L'esercizio in questione richiede di calcolare il valore di $ k $ di un vettore uniformemente distribuito sul seguente supporto:
$ R(X,Y) = { (x,y): 0
$ P(X\leq1/2, Y\leq1/4) $ . Ho impostato l'integrale doppio per calcolare la probabilità richiesta in questo modo:
$ int_(0)^(1/2)int_(0)^(1/4-x^2) 3dydx = 1/4 $
Credete sia corretto? Se no, come dovrei impostare gli estremi?
$ R(X,Y) = { (x,y): 0
$ P(X\leq1/2, Y\leq1/4) $ . Ho impostato l'integrale doppio per calcolare la probabilità richiesta in questo modo:
$ int_(0)^(1/2)int_(0)^(1/4-x^2) 3dydx = 1/4 $
Credete sia corretto? Se no, come dovrei impostare gli estremi?
Risposte
no è sbagliato. Se fai il disegno vedi subito come fare: basta calcolare l'area in questione e moltiplicarla per la densità congiunta:
$mathbb{P}[X<1/2;Y<1/4]=3xxint_(0)^(1/2)x^2dx=1/8$
$mathbb{P}[X<1/2;Y<1/4]=3xxint_(0)^(1/2)x^2dx=1/8$
Grazie della risposta!
Immaginavo fosse sbagliato, infatti il volume del solido che ha come area di base la regione al di sotto di $ y=x^2 $ con $ 0
Immaginavo fosse sbagliato, infatti il volume del solido che ha come area di base la regione al di sotto di $ y=x^2 $ con $ 0
Ovviamente sì.
Il fatto che tu stia studiando i vettori aleatori non ti deve far dimenticare i fondamentali:
Nel tuo esercizio i casi possibili sono dati dall'area del triangoloide della traccia: $1/3$ mentre i casi favorevoli sono dati dall'area di interesse....ragionando così non sbagli più.
Edit: prova ad esempio questo
$mathbb{P}[X<1/2,Y<1/4|X+Y<1]$
...per vedere se hai capito il meccanismo
Il fatto che tu stia studiando i vettori aleatori non ti deve far dimenticare i fondamentali:
$("#Casi favorevoli ")/("#Casi possibili ")$
Nel tuo esercizio i casi possibili sono dati dall'area del triangoloide della traccia: $1/3$ mentre i casi favorevoli sono dati dall'area di interesse....ragionando così non sbagli più.
Edit: prova ad esempio questo
$mathbb{P}[X<1/2,Y<1/4|X+Y<1]$
...per vedere se hai capito il meccanismo
I casi favorevoli sono rappresentati dal volume precedente $ (1/8) $, mentre i casi possibili li ottengo risolvendo il sistema:
$ x^2=y, x+y=1 $,
calcolando l'integrale da $ 0 $ alla $ x $ trovata ( $ (sqrt(5) -1)/2 $ ) e moltiplicando per la densità $ (3) $.
$ x^2=y, x+y=1 $,
calcolando l'integrale da $ 0 $ alla $ x $ trovata ( $ (sqrt(5) -1)/2 $ ) e moltiplicando per la densità $ (3) $.
sicuro di aver letto per bene ciò che ho scritto? Guarda che io per rispondere ci perdo del tempo per spiegarti cose che so già.....
I casi favorevoli sono gli stessi di prima...quindi $1/24$ non $1/8$....$1/8$ era il rapporto fra casi favorevoli e possibili..
Per calcolare la probabilità devi fare il rapporto fra aree
(click me!)
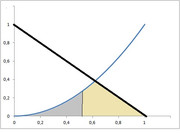
quindi ottieni
casi favorevoli: $int_(0)^(1/2)x^2dx=1/24$
casi possibili: $int_(0)^((sqrt(5)-1)/2)x^2dx+[1-(sqrt(5)-1)/2]^2*1/2=0.1516$
quindi, salvo errori di calcolo, il risultato è $(1/24)/(0.1516)=0.2748$

I casi favorevoli sono gli stessi di prima...quindi $1/24$ non $1/8$....$1/8$ era il rapporto fra casi favorevoli e possibili..
Per calcolare la probabilità devi fare il rapporto fra aree
(click me!)

quindi ottieni
casi favorevoli: $int_(0)^(1/2)x^2dx=1/24$
casi possibili: $int_(0)^((sqrt(5)-1)/2)x^2dx+[1-(sqrt(5)-1)/2]^2*1/2=0.1516$
quindi, salvo errori di calcolo, il risultato è $(1/24)/(0.1516)=0.2748$

Hai ragione! Ho risposto di fretta e non ho considerato l'area del triangolo rettangolo, che è all'interno del supporto e contiene punti che soddisfano $ X+Y<1 $.
Per quanto riguarda la scelta di considerare il $ "#Casi favorevoli " =$ $ 1/8 $ invece che $ 1/24 $, ho semplicemente moltiplicato per $3$ considerando il volume invece dell'area: facendo lo stesso con il denominatore il risultato rimane invariato.
Per quanto riguarda la scelta di considerare il $ "#Casi favorevoli " =$ $ 1/8 $ invece che $ 1/24 $, ho semplicemente moltiplicato per $3$ considerando il volume invece dell'area: facendo lo stesso con il denominatore il risultato rimane invariato.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo