[Scienza delle Costruzioni] - Iperstatico, metodo forze. Passaggi
Buonasera! 
Vorrei alcuni pareri sulla risoluzione di questo iperstatico, svolto graficamente con il metodo delle forze.
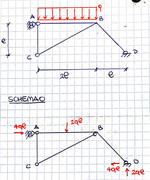
La struttura è la seguente:
Ho studiato quindi 2 schemi isostatici (applico poi il P.S.E.): schema 0 e schema 1.
Schema 0:
Schema 1:
Ho dei dubbi sullo schema 0. Ho ragionato così: Per prima cosa, essendo isostatico esternamente, ho trovato l'equilibrio globale e dopo ho trovato le reazioni vincolari interne. Il pendolo in G potrebbe prendere la forza \( Fx \) ma visto che a sinistra nessun vincolo "può prendere" una forza orizzontale ho ipotizzato che fosse scarico; così la reazione orizzontale di \( Fx \) va direttamente al carrello. Per quanto riguarda l'altro tratto: la forza \( Fy \) va opposta in C, passando all'asta CB si scarica poi sul bipendolo.
Consigli?
P.s. Quale altro vincolo potevo sostituire/declassare?
Vorrei alcuni pareri sulla risoluzione di questo iperstatico, svolto graficamente con il metodo delle forze.
La struttura è la seguente:
Ho studiato quindi 2 schemi isostatici (applico poi il P.S.E.): schema 0 e schema 1.
Schema 0:
Schema 1:
Ho dei dubbi sullo schema 0. Ho ragionato così: Per prima cosa, essendo isostatico esternamente, ho trovato l'equilibrio globale e dopo ho trovato le reazioni vincolari interne. Il pendolo in G potrebbe prendere la forza \( Fx \) ma visto che a sinistra nessun vincolo "può prendere" una forza orizzontale ho ipotizzato che fosse scarico; così la reazione orizzontale di \( Fx \) va direttamente al carrello. Per quanto riguarda l'altro tratto: la forza \( Fy \) va opposta in C, passando all'asta CB si scarica poi sul bipendolo.
Consigli?P.s. Quale altro vincolo potevo sostituire/declassare?
Risposte
"octopus93":
Ho dei dubbi sullo schema 0. Ho ragionato così: Per prima cosa, essendo isostatico esternamente, ho trovato l'equilibrio globale e dopo ho trovato le reazioni vincolari interne. Il pendolo in G potrebbe prendere la forza \( Fx \) ma visto che a sinistra nessun vincolo "può prendere" una forza orizzontale ho ipotizzato che fosse scarico;
Sicura che, ipoteticamente, a sinistra nessuno potrebbe equilibrare una eventuale reazione orizzontale del pendolo interno?
"octopus93":
Per quanto riguarda l'altro tratto: la forza \( Fy \) va opposta in C, passando all'asta CB si scarica poi sul bipendolo.
Ok.
"octopus93":
P.s. Quale altro vincolo potevo sostituire/declassare?
Quella fatta mi sembra una buona scelta, altrimenti dovresti optare per l'inserimento di sconnessioni nell'anello chiuso. Eviterei.
Grazie mille per la risposta!
A sinistra potrei avere una uguale opposta nel pendolo in G ma non sarei in grado poi di equilibrarla dato che la cerniera in C deve avere la stessa direzione dei pei pendolini del bipendolo in A.
Avevo immagino anche, al posto del pendolo, un quadripendolo, ma credo renda la struttura labile.
A sinistra potrei avere una uguale opposta nel pendolo in G ma non sarei in grado poi di equilibrarla dato che la cerniera in C deve avere la stessa direzione dei pei pendolini del bipendolo in A.
Avevo immagino anche, al posto del pendolo, un quadripendolo, ma credo renda la struttura labile.
Prego...
ma questo:
direi anche no. Ti avevo chiesto se eri proprio sicura che a sinistra non ci sono vincoli che potrebbero equilibrare una reazione orizzontale del pendolo. E ci sono: la cerniera potrebbe benissimo equilibrare la reazione del pendolo. Quindi non è questo ragionamento che ti porta a concludere che il pendolo non reagisce . Ciò lo si deduce dalla situazione che hai a destra dopo che hai trovato le reazioni esterne.
ma questo:
"octopus93":
A sinistra potrei avere una uguale opposta nel pendolo in G ma non sarei in grado poi di equilibrarla dato che la cerniera in C deve avere la stessa direzione dei pei pendolini del bipendolo in A.
direi anche no
. Ti avevo chiesto se eri proprio sicura che a sinistra non ci sono vincoli che potrebbero equilibrare una reazione orizzontale del pendolo. E ci sono: la cerniera potrebbe benissimo equilibrare la reazione del pendolo. Quindi non è questo ragionamento che ti porta a concludere che il pendolo non reagisce . Ciò lo si deduce dalla situazione che hai a destra dopo che hai trovato le reazioni esterne.
Ti credo ma ho sempre ragionato dalla "fine " perché io da un tratto iperstatico posso dedurre la terra d'azione rima ancora delle reazioni interne. La cerniera in C reagisce con una forza verticale perché segue l'asse dei pendolini. Scusami, non voglio contraddirti. Comunque per capire meglio come procedere, potresti dirmi come ragioni tu dall'inizio alla fine?
Di che ti scusi? Contraddicimi pure (sugnu nuddu miscatu cu nenti 
). Di base, questo:
lo potevi dire per certo solo se il tratto di sinistra non era vincolato anche col pendolo in \(G\). Infatti, a priori, dato bipendolo verticale, cerniera e pendolo, non puoi dire nulla nemmeno sulla direzione della reazione della cerniera. Perché potresti benissimo avere una reazione orizzontale del pendolo che si equilibra con quella della cerniera, una reazione verticale di quest'ultima equilibrata dal bipendolo che a sua volta equilibra tutti i momenti agenti nel tratto.
Io ragionerei così. Trovo anzitutto le reazioni vincolari esterne, perché come hai giustamente osservato la struttura è isostatica per vincoli esterni. Se studio il tratto di sinistra, per i motivi suddetti, non posso concludere nulla di certo. Passo all'altro tratto, che è isostatico, in quanto vincolato con una cerniera (in $C$) e un pendolo (in $G$) e caricato con due forze: quella inclinata applicata in $D$ e la reazione del carrello in $E$. Se non voglio scrivere le equazioni cardinali e procedere col metodo grafico, applico il p.s.e. una volta considerando il carico $F!= 0$ e nulla la reazione e una volta considerando $F=0$ e non nulla la reazione. Procedendo così ottengo che il pendolo non reagisce e la cerniera reagisce solo con una forza verticale. Con queste informazioni passo al tratto di sinistra in cui si osserva banalmente che l'equilibrio è già verificato.
). Di base, questo:"octopus93":
La cerniera in C reagisce con una forza verticale perché segue l'asse dei pendolini.
lo potevi dire per certo solo se il tratto di sinistra non era vincolato anche col pendolo in \(G\). Infatti, a priori, dato bipendolo verticale, cerniera e pendolo, non puoi dire nulla nemmeno sulla direzione della reazione della cerniera. Perché potresti benissimo avere una reazione orizzontale del pendolo che si equilibra con quella della cerniera, una reazione verticale di quest'ultima equilibrata dal bipendolo che a sua volta equilibra tutti i momenti agenti nel tratto.
Io ragionerei così. Trovo anzitutto le reazioni vincolari esterne, perché come hai giustamente osservato la struttura è isostatica per vincoli esterni. Se studio il tratto di sinistra, per i motivi suddetti, non posso concludere nulla di certo. Passo all'altro tratto, che è isostatico, in quanto vincolato con una cerniera (in $C$) e un pendolo (in $G$) e caricato con due forze: quella inclinata applicata in $D$ e la reazione del carrello in $E$. Se non voglio scrivere le equazioni cardinali e procedere col metodo grafico, applico il p.s.e. una volta considerando il carico $F!= 0$ e nulla la reazione e una volta considerando $F=0$ e non nulla la reazione. Procedendo così ottengo che il pendolo non reagisce e la cerniera reagisce solo con una forza verticale. Con queste informazioni passo al tratto di sinistra in cui si osserva banalmente che l'equilibrio è già verificato.
Sono testa dura e non voglio infastidire nessuno, soprattutto chi è qua per aiutarmi
Comunque grazie! Hai ragione. In effetti prima sono partita da destra e poi ho fatto il ragionamento sopra. Diciamo che ho avuto fortuna.
Con le equazioni come imposteresti il problema? Semplicemente con le equazioni cardinali applicate ai 2 tratti? Qui è semplice perché non ho vincoli esterni/interni, ma in tal caso come si fa?
Comunque grazie! Hai ragione. In effetti prima sono partita da destra e poi ho fatto il ragionamento sopra. Diciamo che ho avuto fortuna.
Con le equazioni come imposteresti il problema? Semplicemente con le equazioni cardinali applicate ai 2 tratti? Qui è semplice perché non ho vincoli esterni/interni, ma in tal caso come si fa?
Nessun fastidio.
Con le equazioni mi scriverei le tre di equilibrio esterno per trovare le reazioni di bipendolo e carrello; poi le tre di equilibrio del secondo tratto per trovare le reazioni di cerniera interna e pendolo interno.
Non ho capito.
Con le equazioni mi scriverei le tre di equilibrio esterno per trovare le reazioni di bipendolo e carrello; poi le tre di equilibrio del secondo tratto per trovare le reazioni di cerniera interna e pendolo interno.
"octopus93":
Qui è semplice perché non ho vincoli esterni/interni, ma in tal caso come si fa?
Non ho capito.
Vorrei impostare l'integrale per trovare l'incognita iperstatica, potresti darmi delle delucidazioni
In corrispondenza della molteplicità vincolare eliminata ho una componente di spostamento diversa da quella dello schema originario.
In questo caso, nello schema originario la rotazione \( \varphi G \) è nulla. Nello schema 1 la rotazione \( \varphi G \) è consentita.
\( \vartheta =\varphi G \)
Gli schemi saranno equivalenti cinematicamente se : \( \vartheta =\bar{\vartheta } =0 \)
Ma \( \vartheta \) dipende sia dai carichi esterni sia dalle incognite iperstatiche : \( \vartheta = \vartheta (0)+\vartheta 1 \)
essendo \( \vartheta 1 \) = \( A11\cdot X1 \)
\( \vartheta (0)=\int_{a}^{b} M1(z)M0(z)/EI\, dz \)
\( A11= \int_{a}^{b} M1(z)M1(z)/EI\, dz \)
Dove M1 ed M0 sono i valori di momenti che ho rispettivamente nello schema 1 e nello schema 0. La mia domanda è : devo aggiungere anche lo sforzo normale N nell'integrale?
Se in un tratto ho una dilatazione termica, moltiplico l'integrale del tratto per il valore di N?
Per un cedimento vincolare cambia solo \( \vartheta =\bar{\delta } \)?
In corrispondenza della molteplicità vincolare eliminata ho una componente di spostamento diversa da quella dello schema originario.
In questo caso, nello schema originario la rotazione \( \varphi G \) è nulla. Nello schema 1 la rotazione \( \varphi G \) è consentita.
\( \vartheta =\varphi G \)
Gli schemi saranno equivalenti cinematicamente se : \( \vartheta =\bar{\vartheta } =0 \)
Ma \( \vartheta \) dipende sia dai carichi esterni sia dalle incognite iperstatiche : \( \vartheta = \vartheta (0)+\vartheta 1 \)
essendo \( \vartheta 1 \) = \( A11\cdot X1 \)
\( \vartheta (0)=\int_{a}^{b} M1(z)M0(z)/EI\, dz \)
\( A11= \int_{a}^{b} M1(z)M1(z)/EI\, dz \)
Dove M1 ed M0 sono i valori di momenti che ho rispettivamente nello schema 1 e nello schema 0. La mia domanda è : devo aggiungere anche lo sforzo normale N nell'integrale?
Se in un tratto ho una dilatazione termica, moltiplico l'integrale del tratto per il valore di N?
Per un cedimento vincolare cambia solo \( \vartheta =\bar{\delta } \)?
"octopus93":
La mia domanda è : devo aggiungere anche lo sforzo normale N nell'integrale?
In generale lo sforzo normale dà un contributo trascurabile. In questo caso hai in un tratto una dilatazione termica assiale, quindi per tale tratto valuti anche lo sforzo normale.
"octopus93":
Se in un tratto ho una dilatazione termica, moltiplico l'integrale del tratto per il valore di N?
No, perché l'integrando è il lavoro interno, quindi integri il prodotto fra lo sforzo normale e la diltazione termica assiale (\(\varepsilon_a^{\mathrm{termica}}= \alpha \cdot \Delta t\))
"octopus93":
Per un cedimento vincolare cambia solo \( \vartheta =\bar{\delta } \)?
Sì.
Ok ti ringrazio! Imposto tutti gli integrali sul quaderno e poi pubblico il procedimento.
CdS schema 0: 
CdS schema 1:
Integrale:
Non ho messo il contributo di N perchè il tratto CD non ha sforzo normale. La dilatazione termica va messa solo in N(0) giusto?
Spero non ci siano errori di calcolo, ho cercato di fare veloce a causa di altri impegni personali
Forse qui si vedono meglio
CdS schema 1:
Integrale:
Non ho messo il contributo di N perchè il tratto CD non ha sforzo normale. La dilatazione termica va messa solo in N(0) giusto?
Spero non ci siano errori di calcolo, ho cercato di fare veloce a causa di altri impegni personali
Forse qui si vedono meglio
A me risultano:
\begin{align*}
\vartheta_1^{(0)} &= \frac{F\,\sqrt{2}\,L^2}{12\,\mathrm{E\,I}}\,, & A_{11} &= \frac{5\,L}{3\,\mathrm{E\,I}}\,.
\end{align*}
Nel calcolo di \(\vartheta_1^{(0)}\) hai fatto un errore nell'ultimo passaggio. Per \(A_{11}\) hai sbagliato il doppio prodotto (penultima riga). Probabilmente colpa della fretta.
P.S. Per il futuro: credo che troverai abbastanza difficilmente qualcuno che si metta a guardare i calcoli...solitamente io nemmeno lo faccio, troppo noioso . Per verificare i conti potresti utilizzare Wolfram Mathematica.
Che significa che la dilatazione va messa solo i N(0)?
\begin{align*}
\vartheta_1^{(0)} &= \frac{F\,\sqrt{2}\,L^2}{12\,\mathrm{E\,I}}\,, & A_{11} &= \frac{5\,L}{3\,\mathrm{E\,I}}\,.
\end{align*}
Nel calcolo di \(\vartheta_1^{(0)}\) hai fatto un errore nell'ultimo passaggio. Per \(A_{11}\) hai sbagliato il doppio prodotto (penultima riga). Probabilmente colpa della fretta.
P.S. Per il futuro: credo che troverai abbastanza difficilmente qualcuno che si metta a guardare i calcoli...solitamente io nemmeno lo faccio, troppo noioso
. Per verificare i conti potresti utilizzare Wolfram Mathematica."octopus93":
Non ho messo il contributo di N perchè il tratto CD non ha sforzo normale. La dilatazione termica va messa solo in N(0) giusto?
Che significa che la dilatazione va messa solo i N(0)?
Intanto grazie! Ricontrolleròi calcoli più tardi, immaginavo ci fossero errori 
Per quanto riguarda la dilatazione, va messa nell'integrale di teta 0, giusto? Non in A11
Per quanto riguarda la dilatazione, va messa nell'integrale di teta 0, giusto? Non in A11
Sì (scusa, non avevo capito).
Prego!
Prego!
Ho ricontrollato i calcoli e adesso i risultati coincidono con i tuoi (errori banali), grazie.
Quindi si ottieneun valore di \( X1={\frac{-\varphi G }{A11}} = {\frac{3\sqrt{2} Fl }{10}} \)
L'impostazione degli integrali è corretta? In questo caso è normale che la dilatazione non compare negli integrali oppure ho sbagliato qualcosa nelle caratteristiche di sollecitazione?
Altra domanda: se lo sforzo normale dove ho la dilatazione non fosse stato nullo avrei messo il termine nell'integrale Teta 0; automaticamente dovevo mettere anche il contributo di quel tratto (senza la dilatazione, visto che va solo in teta0) dello sforzo normale anche in A11?
Non so se mi sono spiegata...
Quindi si ottieneun valore di \( X1={\frac{-\varphi G }{A11}} = {\frac{3\sqrt{2} Fl }{10}} \)
L'impostazione degli integrali è corretta? In questo caso è normale che la dilatazione non compare negli integrali oppure ho sbagliato qualcosa nelle caratteristiche di sollecitazione?
Altra domanda: se lo sforzo normale dove ho la dilatazione non fosse stato nullo avrei messo il termine nell'integrale Teta 0; automaticamente dovevo mettere anche il contributo di quel tratto (senza la dilatazione, visto che va solo in teta0) dello sforzo normale anche in A11?
Non so se mi sono spiegata...
L’impostazione degli integrali è corretta. La dilatazione non compare nel calcolo di theta perché non hai sforzo normale in quel tratto, dunque il lavoro è nullo. Naturalmente lo sforzo normale andava nel calcolo di $A_{11}$.
Grazie!!
Di nulla, felice di essere d'aiuto!
Ciao JoJo_90! Ad esempio, per questo esercizio non riesco ad impostare le equazioniper trovare l'equilibrio interno. Graficamente non mi viene e volevo avere un'alternativa. Ma essendoci vincoli interni/esterni non so come trattarli...
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo