[Elettronica] Analisi Amplificatore Differenziale

[HeroGian]

$ V^{-} = V_1 + (V_o - V_1) \frac{R_1}{R_1 + R_2} $Salve, ho un dubbio riguardante un passaggio necessario all'analisi di un amplificatore differenziale ideale:



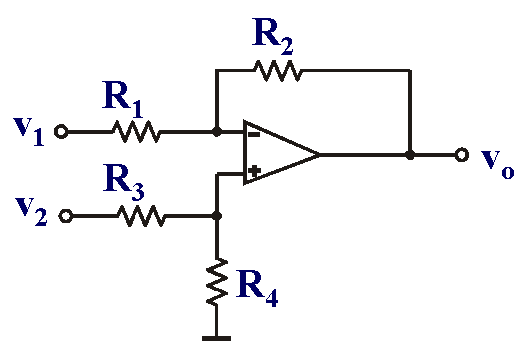
Il mio dubbio riguarda il calcolo della tensione $V^{-}$ presente sul morsetto invertente:
supponendo che la corrente vada da $V_1$ a $V_o$: $I = \frac{V_i - Vo}{R_1 + R_2}$
la tensione ai capi di $R_1$: $V^{-} = R_1I$
sostituendo la prima nella seconda mi viene: $V^{-} = \frac{R_1}{R_1 + R_2}(V_1 - V_o)$

mentre il risultato riportato sul libro è: $V^{-} = V_1 + (V_o - V_1) \frac{R_1}{R_1 + R_2}$ non mi è chiaro perché c'è anche un $+V_1$ nella formula e perché $V_1 e V_o$ hanno segno opposto.
grazie

[Flamber]

Quella che è riportata come soluzione sul libro dovrebbe essere $V_1-V_-$, cioè la tensione che cade sul resistore 1

[RenzoDF]

"HeroGian":... Il mio dubbio riguarda il calcolo della tensione $V^{-}$ presente sul morsetto invertente:

Ti ricordo che quando parli di tensione di un punto vai implicitamente a riferirti alla sua tensione rispetto al riferimento a zero, ovvero come si suol dire, rispetto "a massa".

"HeroGian":... supponendo che la corrente vada da $V_1$ a $V_o$: $I = \frac{V_1 - Vo}{R_1 + R_2}$

Non devi considerarla una ipotesi, ma una scelta di verso, che è del tutto arbitraria ma in ogni caso corretta; comunque ok per la formula della corrente.

"HeroGian":...
la tensione ai capi di $R_1$: $V^{-} = R_1I$

Sì, $R_1I$ è proprio la tensione ai capi di R1, ma non è uguale alla tensione $V^(-)$ fra il morsetto invertente e massa in quanto $V^(-)$ sarà pari alla differenza fra $V_1$ e la tensione $R_1I$ su R1 che, vista la scelta per il verso di $I$, avrà il positivo a sinistra del resistore.

$V^(-)=V_1-R_1I$

"HeroGian":... non mi è chiaro perché c'è anche un $+V_1$ nella formula e perché $V_1 e V_o$ hanno segno opposto.
grazie

Si deve sommare $V_1$ perché, "partendo" dal riferimento a zero, per "arrivare" al morsetto invertente, dovremo prima elettricamente "salire" di $V_1$ e poi "scendere" di $R_1I$.

"HeroGian":... e perché $V_1 e V_o$ hanno segno opposto.

Hanno segno opposto perché il libro sceglie il verso opposto (al tuo) per la corrente, e quindi il testo andrà a sommare e non a sottrarre la tensione $R_1I$ alla $V_1$.

Ora non rimarrà che uguagliare il suddetto potenziale $V^(-)$ al potenziale del morsetto non invertente $V^(+)$, ricavato via partizione della tensione di ingresso $V_2$ su $R_3$ e $R_4$, al fine di determinare la relazione fra le due tensioni di ingresso $V_1$ e $V_2$ e la tensione d'uscita $V_o$.

[HeroGian]

Tutto chiaro ora, grazie mille!