Controlli Automatici: Bode, Nyquist, Matlab
Ragazzi buona sera a tutti. Illustro subito il mio primo dubbio
Supponiamo di avere la seguente funzione di trasferimento: $ G(s) = frac{1}{1+j\omega} $ e di volerne tracciare il diagramma di NYQUIST.
Ora questa G, seppur semplice, vorrei capirla bene, in quanto mi sfugge che ruolo giochi la fase nel tracciamento del diagramma di Nyquist, tracciando il diagramma di Bode riguardo la fase si vede subitissimo che essa è compresa tra 0 e -90 gradi. L'informazione che io quindi dalla fase è solo il "dove sta" il grafico? cioè non posso vedere altro, ad esempio riguardo l'angolazione con cui parte il diagramma per dire non lo si può intuire in qualke modo?
Supponiamo di avere la seguente funzione di trasferimento: $ G(s) = frac{1}{1+j\omega} $ e di volerne tracciare il diagramma di NYQUIST.
Ora questa G, seppur semplice, vorrei capirla bene, in quanto mi sfugge che ruolo giochi la fase nel tracciamento del diagramma di Nyquist, tracciando il diagramma di Bode riguardo la fase si vede subitissimo che essa è compresa tra 0 e -90 gradi. L'informazione che io quindi dalla fase è solo il "dove sta" il grafico? cioè non posso vedere altro, ad esempio riguardo l'angolazione con cui parte il diagramma per dire non lo si può intuire in qualke modo?
Risposte
Le informazioni per il diagramma di Nyquist sono tutte racchiuse in quello di Bode. Anzi, direi che (escludendo altri metodi particolarmente onerosi) il diagramma di Nyquist si disegna tramite quello di Bode. Nel caso di $G(j omega)=1/(1+ j omega)$ fai queste considerazioni:
1- modulo iniziale: 0 dB $to$ 1 in lineare.
2- modulo finale: $-oo$ dB $to$ 0 in lineare
3- fase iniziale: 0. Considerando anche il punto 1 ottieni che il diagramma inizia con $1*e^(j 0)=1+j0$
4- Considerando che, visto il punto 2, il diagramma termina nell'origine, l'informazione sulla fase finale ti dice "come" il diagramma arriva nell'origine. Nel tuo caso tale fase è $-pi/2$, quindi il diagramma arriva in 0 in maniera verticale formando un angolo di $-90^("o")$ con l'asse reale.
5- poichè sia la fase che il modulo decrescono con monotonia non avrai "cappi" o altre stranezze.
In conclusione, il diagramma è un semicerchio che sta nel 2° quadrante del piano complesso. Completandolo trovi un cerchio completo (non dimenticare il verso di percorrenza!)
1- modulo iniziale: 0 dB $to$ 1 in lineare.
2- modulo finale: $-oo$ dB $to$ 0 in lineare
3- fase iniziale: 0. Considerando anche il punto 1 ottieni che il diagramma inizia con $1*e^(j 0)=1+j0$
4- Considerando che, visto il punto 2, il diagramma termina nell'origine, l'informazione sulla fase finale ti dice "come" il diagramma arriva nell'origine. Nel tuo caso tale fase è $-pi/2$, quindi il diagramma arriva in 0 in maniera verticale formando un angolo di $-90^("o")$ con l'asse reale.
5- poichè sia la fase che il modulo decrescono con monotonia non avrai "cappi" o altre stranezze.
In conclusione, il diagramma è un semicerchio che sta nel 2° quadrante del piano complesso. Completandolo trovi un cerchio completo (non dimenticare il verso di percorrenza!)
non ho ben capito, anche se ovviamente è corretto come fai a capire l'angolo di partenza quale sia, non la fase iniziale che è relativa al punto, ma alla tangente alla curva nel punto iniziale
Sinceramente non mi ero mai posto il problema della tangente al diagramma nel punto di partenza. In questo caso puoi ragionare per simmetria, in questo senso:
- il diagramma termina in $0$ con fase $-90$;
- il diagramma di Bode delle fasi è simmetrico (rispetto al polo $s=-1$),
quindi il diagramma di Nyquist parte da $1$ in maniera verticale, esattamente come arriva.
Queste considerazioni vengono spontanee dopo un pò di tentativi: prova a disegnare diagrammi sempre più complessi. Mi ricordo che sbagliavo sempre, poi mi si è accesa una lampadina e da lì non ho più sbagliato un diagramma... Ricorda che il diagramma dei moduli porta in genere poca informazione (grosso modo decresce), mentre quello delle fasi è fondamentale. Ad esempio, se il diagramma di Bode delle fasi attraversa $"arg"F(j omega) = pi$ sai che lì c'è un attraversamento della semiretta reale negativa (che poi si rivela molto importante per le considerazioni sulla stabilità)
- il diagramma termina in $0$ con fase $-90$;
- il diagramma di Bode delle fasi è simmetrico (rispetto al polo $s=-1$),
quindi il diagramma di Nyquist parte da $1$ in maniera verticale, esattamente come arriva.
Queste considerazioni vengono spontanee dopo un pò di tentativi: prova a disegnare diagrammi sempre più complessi. Mi ricordo che sbagliavo sempre, poi mi si è accesa una lampadina e da lì non ho più sbagliato un diagramma... Ricorda che il diagramma dei moduli porta in genere poca informazione (grosso modo decresce), mentre quello delle fasi è fondamentale. Ad esempio, se il diagramma di Bode delle fasi attraversa $"arg"F(j omega) = pi$ sai che lì c'è un attraversamento della semiretta reale negativa (che poi si rivela molto importante per le considerazioni sulla stabilità)
hmmm penso di aver capito, una sorta di "l'esperienza insegna". In ogni caso il diagramma di fase lo faccio sempre, cioè reputo sia il piu utile dei due.
Wela ragazzi i'm back, una domanda. Qualkuno può spiegarmi bene cosa c'entra lo sviluppo in serie di taylor per determinare gli asintoti parabolici nei diagrammi di nyquist? E poi...Sti asintoti si hanno solo per $\omega = 0$?
Ti faccio un esempio (a te la generalizzazione... 
): supponi di avere $G(s)=1/(s^2(1-s tau))$. Allora
$"Re"[G(j omega)]=(-1)/(omega^2+omega^4 tau^2)$,
$"Im"[G(j omega)]=(-tau)/(omega+omega^3 tau^2)$.
Ma se $omega to 0$ allora $"Re"[G(j omega)] ~= -1/omega^2$ e $"Im"[G(j omega)]~= -tau/omega$, quindi le equazioni parametriche dell'asintoto sono
${(x=-1/omega^2),(y=-tau/omega):}$ $\quad \quad rArr \quad quad$ $x=-1/(tau^2)*y^2$,
che è la famosa parabola. Come vedi è un discorso di infinitesimi di ordine superiore più che un'applicazione delle serie di Taylor.
In risposta alla seconda domanda: gli asintoti si hanno solo quando il sistema presenta poli di ordine $>=1$ nell'origine, e quindi per $omega to 0$.
): supponi di avere $G(s)=1/(s^2(1-s tau))$. Allora$"Re"[G(j omega)]=(-1)/(omega^2+omega^4 tau^2)$,
$"Im"[G(j omega)]=(-tau)/(omega+omega^3 tau^2)$.
Ma se $omega to 0$ allora $"Re"[G(j omega)] ~= -1/omega^2$ e $"Im"[G(j omega)]~= -tau/omega$, quindi le equazioni parametriche dell'asintoto sono
${(x=-1/omega^2),(y=-tau/omega):}$ $\quad \quad rArr \quad quad$ $x=-1/(tau^2)*y^2$,
che è la famosa parabola. Come vedi è un discorso di infinitesimi di ordine superiore più che un'applicazione delle serie di Taylor.
In risposta alla seconda domanda: gli asintoti si hanno solo quando il sistema presenta poli di ordine $>=1$ nell'origine, e quindi per $omega to 0$.
Sinceramente mi viene difficile disegnarmi un'asintoto parabolico...cioè non lo visualizzo diciamo potresti tracciarmi il grafico, per fila e per segno di...
$G(s) = frac{1}{s^2(s+1)}$ in analogia al tuo esempio cioè, se il polo nell'origine è del primo grado allora traccio la retta e vai con l'asintoto ma in questo caso?
(il discorso di taylor l'ho capito cmq)
$G(s) = frac{1}{s^2(s+1)}$ in analogia al tuo esempio cioè, se il polo nell'origine è del primo grado allora traccio la retta e vai con l'asintoto ma in questo caso?
(il discorso di taylor l'ho capito cmq)
In questo caso viene facile facile, infatti il diagramma coincide in pratica con la parabola $x=-y^2$, dove $x="Re"G(j omega)$, $y="Im" G(j omega)$:
Un esempio un pò più articolato: prendi $G(s)=1/s^2 ((1+0.1s))/((1+s))$, che ha questo diagramma di Bode:
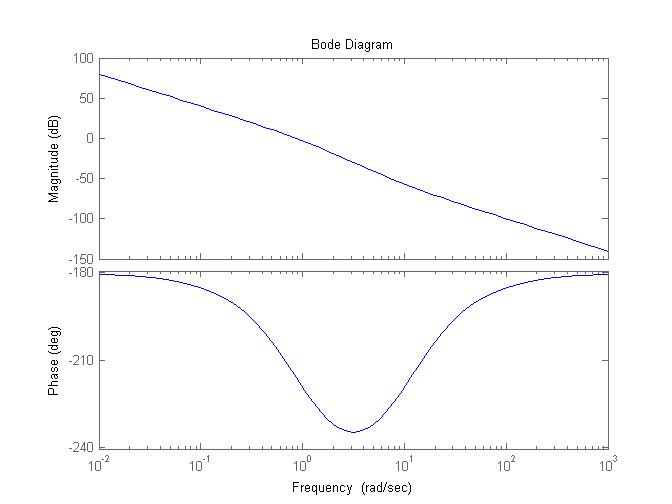
Visto "da lontano" il diagramma di Nyquist è praticamente lo stesso della fdt precedente, ma andando a zoomare nei pressi dell'origine si trova questo:
come era predicibile dal diagramma di Bode delle fasi, che vale $- pi$ (andamento "piatto") per $omega to +oo$.
C'è poi il problema della chiusura all'infinito. La regola "a spanne" è: tanti mezzi giri in senso orario quanti sono i poli nell'origine, partendo da $omega=0^-$ e terminando in $omega=0^+$. Ecco un'immagine qualitativa della situazione:
Un esempio un pò più articolato: prendi $G(s)=1/s^2 ((1+0.1s))/((1+s))$, che ha questo diagramma di Bode:
Visto "da lontano" il diagramma di Nyquist è praticamente lo stesso della fdt precedente, ma andando a zoomare nei pressi dell'origine si trova questo:
come era predicibile dal diagramma di Bode delle fasi, che vale $- pi$ (andamento "piatto") per $omega to +oo$.
C'è poi il problema della chiusura all'infinito. La regola "a spanne" è: tanti mezzi giri in senso orario quanti sono i poli nell'origine, partendo da $omega=0^-$ e terminando in $omega=0^+$. Ecco un'immagine qualitativa della situazione:
La pratica insegna...sempre così ahime...
I'm back, una curiosità non c'è un modo per impostare matlab a farmi partire i diagrammi da 0 al posto di -360 gradi per la fase? mi spiego...se io ho $G(s) = frac{1}{s^2+1}$ per me per $\omega -> 0$ va a 0 per valori alti va a -180, per matlab invece parte da -360 e poi va a -180, e sta cosa si riflette su nyquist pure. Non c'è un modo per impostarlo? grazie
Altra cosa, più importante, come traccereste voi il diagramma di nyquist della seguente funzione...
$G(s) = frac{10s+1}{(s-1)^2*(s^2+1)}$
Io lo sto facendo ora, voi ditemi come lo fareste così poi lo confronto, grazie per la disponibilità
$G(s) = frac{10s+1}{(s-1)^2*(s^2+1)}$
Io lo sto facendo ora, voi ditemi come lo fareste così poi lo confronto, grazie per la disponibilità
"Lauke":
I'm back, una curiosità non c'è un modo per impostare matlab a farmi partire i diagrammi da 0 al posto di -360 gradi per la fase? mi spiego...se io ho $G(s) = frac{1}{s^2+1}$ per me per $\omega -> 0$ va a 0 per valori alti va a -180, per matlab invece parte da -360 e poi va a -180, e sta cosa si riflette su nyquist pure. Non c'è un modo per impostarlo? grazie
Facendolo con Matlab, mi parte da 0°. Gli ho dato i comandi
H=tf([1],[1 0 1]) bode(H) nyquist(H)
Comunque vanno bene entrambe le versioni, non v'è differenza alcuna fra -360° e 0°. Piuttosto occhio al diagramma di Nyquist, a me Matlab lo disegna sbagliato. Quello vero si spalma su tutto l'asse reale (la fdt non ha una parte immaginaria) tranne il segmento $]0,1"[" $.
Riguardo l'altro, c'è solo da ragionare coi diagrammi di Bode (stavolta anche quello del modulo!!!). Tra l'altro mi sto rendendo conto di quanto Matlab sia scarso nel disegnare i diagrammi di Nyquist: lo sbaglia del tutto! Prova ancora, se hai problemi ti faccio vedere come l'ho fatto io.
Lo stesso non va...ho provato a utilizzare scilab, che mi fa bode correttamente nella fase...ma nel modulo nisba, e manco voglio perderci tempo. Per matlab bhu non ho idea di come fare, la sintassi che utilizzo è pari a quella tua per cui non so cosa fare
wei ragazzi allora...finalmente ho imparato a farmi i diagrammi di nyquist...Problema successivo a questo è il diagramma completo di nyquist, ai fini dell'applicazione del criterio di nyquist...Allora supponiamo di avere la seguente funzione di trasferimento:
$G(s) = frac{(1+s)*(1+0.1s)*(1+0.01s)}{s^4}$ la quale c'ha un suo diagramma ecc...Ora per il farne il diagramma completo, a mano e magari mi dite pure se si può fare con matlab. Ho un problema cioè non mi viene il raccordo diciamo. Poichè il polo all'origine è solo 1 ma con molteplicità 4 dovrei avere un raccordo con una fase nel totale di 180*4 = 720 gradi...Il problema, un blocco mentale più che altro è che bhu non riesco a farlo non è che qualkuno può mostrarmi come farlo nella $G(s)$ da me proposta? vi ringrazio
$G(s) = frac{(1+s)*(1+0.1s)*(1+0.01s)}{s^4}$ la quale c'ha un suo diagramma ecc...Ora per il farne il diagramma completo, a mano e magari mi dite pure se si può fare con matlab. Ho un problema cioè non mi viene il raccordo diciamo. Poichè il polo all'origine è solo 1 ma con molteplicità 4 dovrei avere un raccordo con una fase nel totale di 180*4 = 720 gradi...Il problema, un blocco mentale più che altro è che bhu non riesco a farlo non è che qualkuno può mostrarmi come farlo nella $G(s)$ da me proposta? vi ringrazio
Mi va di divertirmi un pò... Ovviamente è fuori scala, il cappio nei pressi dell'origine in realtà non si vede "a occhio nudo" ma come ben saprai se non ne tieni conto farai considerazioni errate sulla stabilità. In arancione le frequenze positive, in verde le negative, in rosso la chiusura all'infinito, a matita l'asintoto quartico.
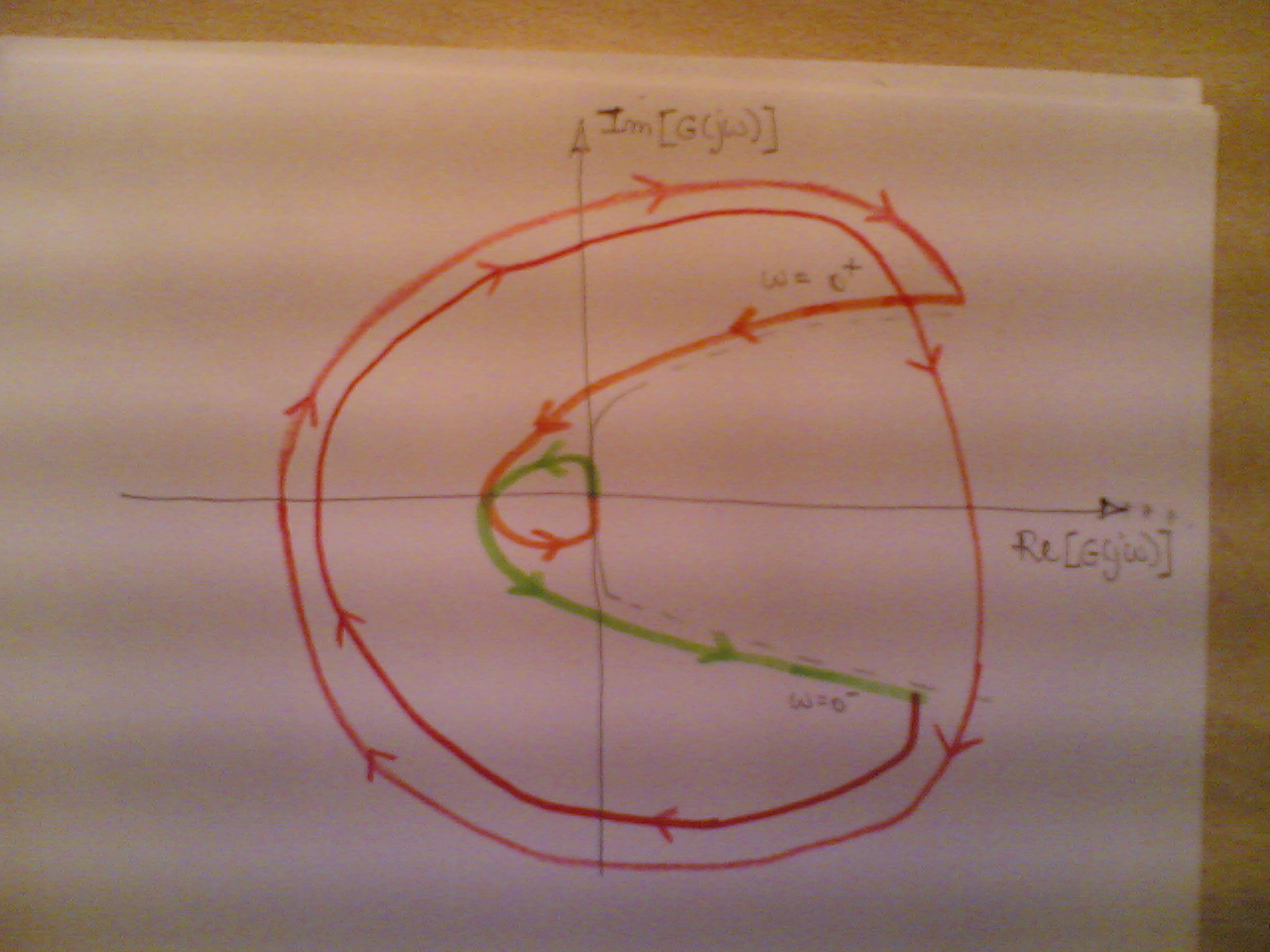
Wella ragazzi altra funzione di cui farne il diagramma di Nyquist, ovviamente matlab bhu lo fa a modo suo...
la fdt è...$G(s) = frac{s+10}{(s+0.1)*(s^2+1)}$ che dalla teoria che ho studiato dovrebbe avere un'asintoto obliqui e per quanto riguarda la fase ho
fase iniziale ]0,-90[ e poi, poichè mi spunta un salto nel diagramma di fase ]-270,-180[.
per cui il grafico con $\omega in [0,+infty]$ dovrebbe prendersi il quarto e il secondo quadrante (in successione) cosa che matlab non mi fa potreste postarmi il diagramma di questa funzione fatta da voi? Grazie tante
la fdt è...$G(s) = frac{s+10}{(s+0.1)*(s^2+1)}$ che dalla teoria che ho studiato dovrebbe avere un'asintoto obliqui e per quanto riguarda la fase ho
fase iniziale ]0,-90[ e poi, poichè mi spunta un salto nel diagramma di fase ]-270,-180[.
per cui il grafico con $\omega in [0,+infty]$ dovrebbe prendersi il quarto e il secondo quadrante (in successione) cosa che matlab non mi fa potreste postarmi il diagramma di questa funzione fatta da voi? Grazie tante
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo