Verso della normale uscente dal piano
ciao a tutti,
il mio problema è, credo, semplice, ma non riesco a capire comunque come fare. Come posso, data l'equazione di un piano con relativi parametri a,b,c,d, individuare il verso della normale uscente dal piano stesso?
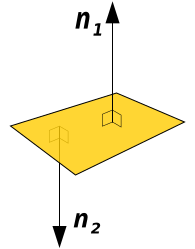
Come capire se ho a che fare con n1 o con n2? Grazie
il mio problema è, credo, semplice, ma non riesco a capire comunque come fare. Come posso, data l'equazione di un piano con relativi parametri a,b,c,d, individuare il verso della normale uscente dal piano stesso?

Come capire se ho a che fare con n1 o con n2? Grazie
Risposte
Ciao.
Cerco di esprimere il mio punto di vista sul problema posto.
E' noto che, data l'equazione generale in forma cartesiana del piano nello spazio
$ax+by+cz+d=0$, con $(a,b,c)!=(0,0,0)$
si ottiene che il vettore $(a,b,c)$ ha direzione normale al piano.
In realtà tutti i vettori del tipo $k(a,b,c)$, con $k!=0$ continueranno a essere normali al piano, visto che il prodotto tra uno scalare (non nullo) e un vettore (non nullo) conserva la direzione del vettore; ciò è coerente con il fatto che, moltiplicando entrambi i membri dell'equazione del piano per una costante $k!=0$, si otterrebbe una nuova equazione dello stesso piano, cioè le equazioni
$ax+by+cz+d=0$
$kax+kby+kcz+kd=0$
sono equazioni differenti (sottointendendo $k!=1$), ma sono equivalenti e, quindi, riferite allo stesso piano.
In particolare, qualora si considerasse $k<0$, il vettore normale $k(a,b,c)$ risulterebbe avere verso opposto al vettore originale $(a,b,c)$.
In conclusione, il problema posto non ha una risposta ben definibile, a meno che non ci si riferisca in senso stretto a una quaterna fissata di parametri $(a,b,c,d)$ relativa al piano.
Riassumendo: considerando il piano come ente geometrico, direi che non esiste un verso preferenziale di uscita dal piano del vettore normale (i versi possibili di uscita in direzione normale sono due), mentre rispetto all'equazione in forma cartesiana del piano
$ax+by+cz+d=0$, con $(a,b,c)!=(0,0,0)$
si potrebbe assumere, come verso preferenziale (ma sarebbe un fatto puramente convenzionale), quello indicato dal vettore $(a,b,c)$.
Saluti.
Cerco di esprimere il mio punto di vista sul problema posto.
E' noto che, data l'equazione generale in forma cartesiana del piano nello spazio
$ax+by+cz+d=0$, con $(a,b,c)!=(0,0,0)$
si ottiene che il vettore $(a,b,c)$ ha direzione normale al piano.
In realtà tutti i vettori del tipo $k(a,b,c)$, con $k!=0$ continueranno a essere normali al piano, visto che il prodotto tra uno scalare (non nullo) e un vettore (non nullo) conserva la direzione del vettore; ciò è coerente con il fatto che, moltiplicando entrambi i membri dell'equazione del piano per una costante $k!=0$, si otterrebbe una nuova equazione dello stesso piano, cioè le equazioni
$ax+by+cz+d=0$
$kax+kby+kcz+kd=0$
sono equazioni differenti (sottointendendo $k!=1$), ma sono equivalenti e, quindi, riferite allo stesso piano.
In particolare, qualora si considerasse $k<0$, il vettore normale $k(a,b,c)$ risulterebbe avere verso opposto al vettore originale $(a,b,c)$.
In conclusione, il problema posto non ha una risposta ben definibile, a meno che non ci si riferisca in senso stretto a una quaterna fissata di parametri $(a,b,c,d)$ relativa al piano.
Riassumendo: considerando il piano come ente geometrico, direi che non esiste un verso preferenziale di uscita dal piano del vettore normale (i versi possibili di uscita in direzione normale sono due), mentre rispetto all'equazione in forma cartesiana del piano
$ax+by+cz+d=0$, con $(a,b,c)!=(0,0,0)$
si potrebbe assumere, come verso preferenziale (ma sarebbe un fatto puramente convenzionale), quello indicato dal vettore $(a,b,c)$.
Saluti.
ti ringrazio davvero della risposta completa, che è un po' la conclusione a cui ero arrivato anche io. Allora preferisco spiegare il perché della domanda: sto cercando di capire in dettaglio il calcolo della distanza di un punto da un piano dato. Ho capito che per farlo devo calcolare il prodotto scalare tra il piano e il punto P.
Inoltre, secondo questa pagina http://www.songho.ca/math/plane/plane.html (ultimo paragrafo "Distance from a Point", ultime righe), ho che, se il prodotto scalare risulta positivo, il punto P si trova dallo stesso lato a cui punta la normale, mentre se risulta negativo si trova dal lato opposto. Ecco, io non riesco allora a capire questa cosa, perché non riesco a capire da che parte "punti" la normale. Spero di avere chiarito il mio dilemma.
Inoltre, secondo questa pagina http://www.songho.ca/math/plane/plane.html (ultimo paragrafo "Distance from a Point", ultime righe), ho che, se il prodotto scalare risulta positivo, il punto P si trova dallo stesso lato a cui punta la normale, mentre se risulta negativo si trova dal lato opposto. Ecco, io non riesco allora a capire questa cosa, perché non riesco a capire da che parte "punti" la normale. Spero di avere chiarito il mio dilemma.
Ciao.
Secondo me al numeratore della relazione per il calcolo di $D$ andrebbe posto il simbolo di valore assoluto; credo che in questo modo tutto il dilemma sarebbe risolto; infatti la distanza $D$ non può assumere valori negativi.
Saluti.
Secondo me al numeratore della relazione per il calcolo di $D$ andrebbe posto il simbolo di valore assoluto; credo che in questo modo tutto il dilemma sarebbe risolto; infatti la distanza $D$ non può assumere valori negativi.
Saluti.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo