$S^1\vee S^1$ ha rivestimento universale contraibile?

[killing_buddha]

Rispondendo qui ho implicitamente usato questa cosa, ma non mi sembra ovvio dimostrarlo né falsificarlo, né trovo un riferimento online.

Perciò: è vero o falso che il rivestimento universale di $S^1\vee S^1$, ovvero il grafo di Cayley

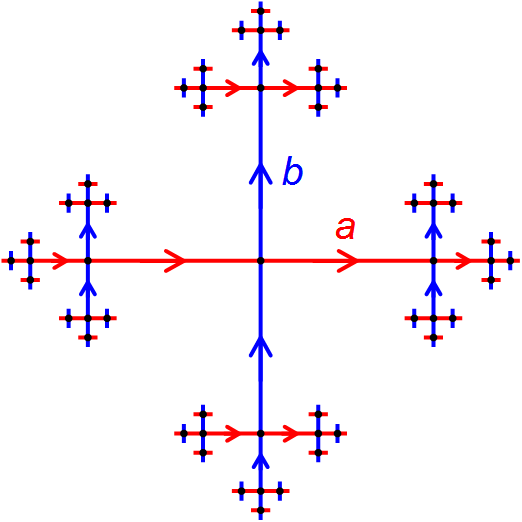
è uno spazio contraibile?

[spugna2]

Provo a dare un'idea, ma non garantisco che funzioni: per ogni $n in NN$ chiamo $X_n$ il sottografo costituito dai vertici che si raggiungono dal centro con al più $n$ passi, e osservo che $X_(n+1)$ si retrae su $X_n$; esiste inoltre una retrazione (non per deformazione) $r_n:X rightarrow X_n$ che manda ogni $x in X setminus X_n$ nell'unico "estremo" di $X_n$ che sconnette $x$ dal centro. Costruisco allora $F:X times [0,1] rightarrow X$ tale che $F(*,0)$ sia l'identità e che $F(*,1)$ mandi tutto nel centro: per ogni $n in NN$ definisco $F$ in $X times [1/(n+2),1/(n+1)]$ come la composizione di $r_(n+1) times id$ con la retrazione di $X_(n+1)$ su $X_n$, e infine pongo $F(x,0)=x$. La continuità in $X times (0,1]$ segue dal lemma di incollamento, mentre quella in $(x,0)$ dovrebbe venire per successioni.