Quesito Grafico: Rotazione di Rette Parallele

[Bacchinif]

Il quesito che sto per porvi è molto banale, e necessita di una risoluzione di tipo grafico, ma, nonostante ciò, non sono riuscito a trovare una quadra:

PROBLEMA

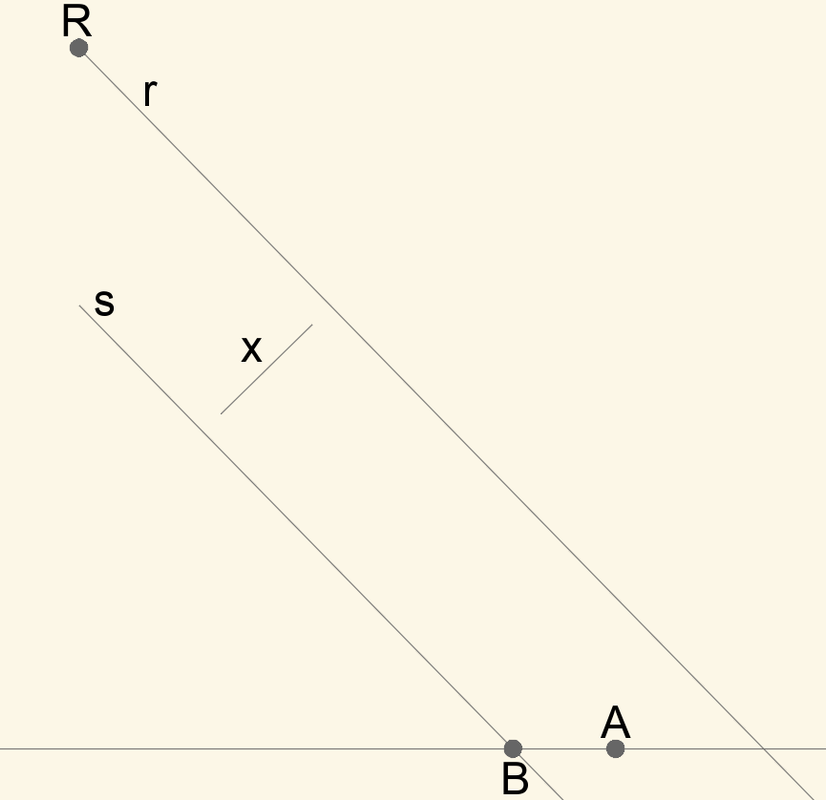
Le rette r ed s sono tra loro parallele e distanti x.
La retta s deve passare per il punto A, rimanendo parallela ed equidistante dalla retta r che a sua volta potrà ruotare solo attorno al punto R (fissato).

[Bokonon]

"Bacchinif":
La retta s deve passare per il punto A, rimanendo parallela ed equidistante dalla retta r che a sua volta potrà ruotare solo attorno al punto R (fissato).

Due rette parallele sono sempre equidistanti.
Se deve passare per A allora è una traslazione, non una rotazione.

[Bacchinif]

"Bokonon":[quote="Bacchinif"]
La retta s deve passare per il punto A, rimanendo parallela ed equidistante dalla retta r che a sua volta potrà ruotare solo attorno al punto R (fissato).

Due rette parallele sono sempre equidistanti.
Se deve passare per A allora è una traslazione, non una rotazione.[/quote]

No. Perché facendo traslare le due rette (cioè, ponendo la s in A) risulterebbe che la retta r non passerebbe più per R.

Il punto R NON appartiene alla retta, ma è la retta a passare per R. Il punto R è lì fissato.

[Bokonon]

Ok, allora B non conta nulla.
Se vuoi ruotarla sopra A, prendi R come l'origine e traccia la circonferenza di raggio raggio RA.
Chiamiamo P il punto di intersezione fra la circonferenza e la retta S.
L'angolo di rotazione è PRA e porta P sopra A.
Tutti gli altri punti di S si portano nel medesimo modo. Prendi ad esempio il punto B e la circonferenza di raggio RB. Ruota RB del medesimo angolo PRA e avrai un altro punto della nuova retta S' che passa per A.
Disegna la retta che passa per PB.
Se ruoti anche la retta R del medesimo angolo vedrai che R' e S' restano parallele (per la verità la retta non serve a nulla, bastano il centro, un luogo di punti e un angolo).