Quadrato non completamente inscritto

[luco89]

Salve
sto preparando lo scritto di Geometria per fisica. Ho trovato quest'esercizio ma non so da dove partire.
Determinare il raggio del cerchio, rappresentato nel disegno seguente, sapendo che il lato del quadrato vale 8.

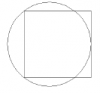
Grazie mille per l'aiuto!

[gio73]

Fico!
Ci voglio provare!
Allora traccerei il segmento che congiunge il punto di tangenza col punto medio del lato opposto. Questo segmento è lungo 8, giusto? (il punto di tangenza è punto medio del quadrato, vero?)
Questo segmento è costituito dal raggio $r$ più una quantità incognita $x$, posto che riuscimo a determinare la posizione del centro della circonferenza potremmo unirla con gli altri due punti, i segmenti che collegano il centro con gli altri due vertici del quadrato comuni alla circonferenza saranno lunghi $r$ e riusciamo quindi a vedere un triangolo isoscele di base 8, lati obliqui $r$ e altezza $x$.
Basteranno queste considerazioni?

[luco89]

Otterremo quindi una situazione del genere

Pur utilizzando il teorema della corda, poiché non conosciamo l'angolo adiacente a X rimane tutto in funzione di R, quindi punto e a capo.
Almeno ora non sto brancolando nel buio!

[vittorino70]

[luco89]

Grazie mille! Non ho lontanamente pensato al teorema di euclide, d'altronde nel programma di Geometria non è stato nemmeno accennato
Grazie ancora!!

[gio73]

Ciao a entrambi,
@vittorino70, non c'è nessuna fretta di esporre una completa soluzione, in fin dei conti l'esercizio è di luco89.
A mio avviso è più proficuo dare un'imbeccata invece di tutta la "cena".
Ad ogni modo la mia soluzione era la seguente.
I condizione
$x+r=8$
$ x=8-r$
$ x^2=64+r^2-16r$

II condizione
$r^2=4^2+x^2$
$r^2=16+64+r^2-16r$
$16r=16+64$
$r=1+4=5$

[vittorino70]

Voglio dare anch'io un consiglio a gio73: non introdurre troppe incognite in un problema. Se pensi che ce ne vogliono due, prova a risolvere il problema con una. Perché più incognite metti, più equazioni devi scrivere... Altrimenti rischi di fare come quello che, per risolvere il problema "trovare la misura del lato di un quadrato il cui perimetro misura 100m " , indica con x,y,z,t la misura dei 4 lati e scrive il sistema:

\(\displaystyle \begin{cases}x=y\\y=z\\z=t\\x+y+z+t=100\end{cases} \)

[gio73]

Spiacente vittorino non colgo l'ironia, ma io come altri non sono il meglio del forum (a tuo giudizio, naturalmente!)

[vittorino70]

Non è ironia la mia.Tu dai un consiglio a me, io uno a te. Spero che tra le regole del Forum non ci sia pure quella di "non dare consigli ai moderatori " !

[Luca.Lussardi]

C'è una differenza: quello che hai detto a gio73 è un consiglio, quello che ti ha detto gio73 è una nostra regola, non è un consiglio; se non ti va di rispettarla non avrai vita facile, noi non dobbiamo mostrare i muscoli ma dobbiamo insegnare a ragionare per quanto ci possiamo riuscire.

[vittorino70]

E' vero, mi sono allontanato dalla linea che impone di dare suggerimenti e non soluzioni preconfezionate. Ma lascia che ti dica che certi "suggerimenti " dovrebbero preoccupare per lo meno quanto le soluzioni complete ( ma forse assai di più).