Grafici di due funzioni: $|x^2+3x+2|$ e $x-[x]$

[Argentino1]

Dovrei disegnare il grafico di queste due funzioni:
$h(x)=|x^2+3x+2|$ e $m(x)=x-[x]$
La prima ho provato a scomporla con ruffini trovando:
$|(x+1)(x+2)|$ ma il grafico non riesco a farlo...

Per la seconda non capisco cosa voglia dire $[x]$

Come posso partire?

[etta.nico]

"Argentino":
La prima ho provato a scomporla con ruffini trovando:
$|(x+1)(x+2)|$ ma il grafico non riesco a farlo...

be direi che è una parabola con concavità verso l'alto. che interseca l'asse delle $x$ in $-1$ e $-2$. ha vertice $(-3/2, 5/4)$ se non ho sbagliato i conti.

"Argentino":
Per la seconda non capisco cosa voglia dire $[x]$

$[x]$ significa la parte intera di x.

[Argentino1]

Il grafico mi risulta essere il seguente... visto che è in modulo;
[asvg]xmin=-10;xmax=10;ymin=-2;ymax=5;
axes();
stroke="dodgerblue"; plot("abs((x+1)(x+2))");[/asvg]
è corretto vero?

[vakoom]

La seconda funzione si chiama "mantissa", la sua rappresentazione è molto semplice (puoi trovarla con una semplice ricerca su google).

[etta.nico]

"Argentino":Il grafico mi risulta essere il seguente... visto che è in modulo;
[asvg]xmin=-10;xmax=10;ymin=-2;ymax=5;
axes();
stroke="dodgerblue"; plot("abs((x+1)(x+2))");[/asvg]
è corretto vero?

perfetto

[Argentino1]

"vakoom":La seconda funzione si chiama "mantissa", la sua rappresentazione è molto semplice (puoi trovarla con una semplice ricerca su google).

Non la trovo...
Dubito sia la seguente...
[asvg]xmin=-10;xmax=10;ymin=-2;ymax=5;
axes();
stroke="dodgerblue"; plot("abs(x-[x])");[/asvg]
giusto (mi riferisco a $x-[x]$)?

[vakoom]

No, decisamente non è quella.



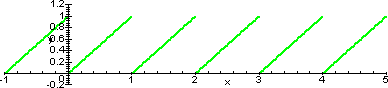
E' questa. Si tratta di una funzione periodica di periodo 1. Se a un numero sottrai la sua parte intera (es: 3,84 - [3.84] = 0.84) ottieni un valore dell'intervallo [0;1)

[Argentino1]

"vakoom":No, decisamente non è quella.



E' questa. Si tratta di una funzione periodica di periodo 1. Se a un numero sottrai la sua parte intera (es: 3,84 - [3.84] = 0.84) ottieni un valore dell'intervallo [0;1)

Ah ok, grazie mille.