Velocità areolare - formule di Binet
Ciao a tutti! Ho qualche dubbio in merito alla deduzione della velocità areolare dall'espressione
\(\displaystyle A'(t) := \frac{1}{2}(P(t)-O) \times v(t) \)
Devo valutare la derivata dell'area spazzata dal raggio vettore durante il moto lungo del punto lungo la traiettoria. Consideriamo il caso in cui la traiettoria giaccia sempre su di un piano. La curva crea una regione con una certa area nel piano della figura, regione compresa tra la curva, l’asse del riferimento polare e il raggio vettore OP.
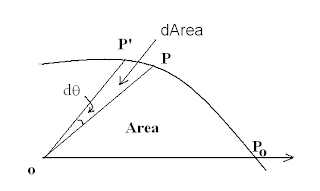
Se la particella si muove, in un certo tempo dt il punto si muove da P a P’. L’area cresce di una quantità dArea, come in figura. Se dt è piccolo, l’arco si confonde con la corda ed è circa uguale all’altezza del triangolo OPP’. Ho che l'’area di questo triangolo è:
\(\displaystyle dArea= \frac{1}{2} r^2dθ \) ma non capisco bene il motivo. Ho fatto una supposizione ma volevo chiedervene conferma:
So che è possibile calcolare l'area di un triangolo mediante la formula \(\displaystyle A = \frac{1}{2} a \cdot b \cdot senθ \)
Allora ho pensato che per valori molto piccoli di dθ è possibile approssimare il prodotto dei lati \(\displaystyle a \cdot b \) a \(\displaystyle r^2 \), ma per quanto riguarda il \(\displaystyle sen(dθ) \) è stato approssimato a \(\displaystyle dθ \) mediante l'uso della formula di taylor al primo ordine?
Inoltre non riesco proprio a spiegarmi un passaggio che ho trovato sugli appunti del mio professore nelle formule di Binet che vi riporto:
Un moto centrale è determinato in maniera univoca dall'orbita \(\displaystyle \rho(θ) \) e dalla costanza della velocità areolare.
Dim. Se è nota \(\displaystyle \rho(θ) \) e \(\displaystyle θ' = \frac{c}{\rho^2} \), allora \(\displaystyle P(θ)-O = \rho(θ)u \), la velocità \(\displaystyle v = \frac{d}{dθ}\rho(θ)\frac{dθ}{dt}u + \rho(θ)θ'u_t= -\frac{d}{dθ}(\frac{c}{\rho})u + \frac{c}{\rho}u_t \)
Infine, per l'accelerazione si ottiene:
\(\displaystyle a = \frac{dv}{dt} = -\frac{d^2}{dθ^2}(\frac{c}{\rho})θ'u -\frac{c}{\rho}θ'u = -[\frac{d^2}{dθ^2} \frac{1}{\rho} + \frac{1}{\rho}]\frac{c^2}{\rho^2}u \)
Non riesco a capire quest'ultima uguaglianza! Spero che qualcuno di voi possa aiutarmi, grazie anticipatamente
\(\displaystyle A'(t) := \frac{1}{2}(P(t)-O) \times v(t) \)
Devo valutare la derivata dell'area spazzata dal raggio vettore durante il moto lungo del punto lungo la traiettoria. Consideriamo il caso in cui la traiettoria giaccia sempre su di un piano. La curva crea una regione con una certa area nel piano della figura, regione compresa tra la curva, l’asse del riferimento polare e il raggio vettore OP.

Se la particella si muove, in un certo tempo dt il punto si muove da P a P’. L’area cresce di una quantità dArea, come in figura. Se dt è piccolo, l’arco si confonde con la corda ed è circa uguale all’altezza del triangolo OPP’. Ho che l'’area di questo triangolo è:
\(\displaystyle dArea= \frac{1}{2} r^2dθ \) ma non capisco bene il motivo. Ho fatto una supposizione ma volevo chiedervene conferma:
So che è possibile calcolare l'area di un triangolo mediante la formula \(\displaystyle A = \frac{1}{2} a \cdot b \cdot senθ \)
Allora ho pensato che per valori molto piccoli di dθ è possibile approssimare il prodotto dei lati \(\displaystyle a \cdot b \) a \(\displaystyle r^2 \), ma per quanto riguarda il \(\displaystyle sen(dθ) \) è stato approssimato a \(\displaystyle dθ \) mediante l'uso della formula di taylor al primo ordine?
Inoltre non riesco proprio a spiegarmi un passaggio che ho trovato sugli appunti del mio professore nelle formule di Binet che vi riporto:
Un moto centrale è determinato in maniera univoca dall'orbita \(\displaystyle \rho(θ) \) e dalla costanza della velocità areolare.
Dim. Se è nota \(\displaystyle \rho(θ) \) e \(\displaystyle θ' = \frac{c}{\rho^2} \), allora \(\displaystyle P(θ)-O = \rho(θ)u \), la velocità \(\displaystyle v = \frac{d}{dθ}\rho(θ)\frac{dθ}{dt}u + \rho(θ)θ'u_t= -\frac{d}{dθ}(\frac{c}{\rho})u + \frac{c}{\rho}u_t \)
Infine, per l'accelerazione si ottiene:
\(\displaystyle a = \frac{dv}{dt} = -\frac{d^2}{dθ^2}(\frac{c}{\rho})θ'u -\frac{c}{\rho}θ'u = -[\frac{d^2}{dθ^2} \frac{1}{\rho} + \frac{1}{\rho}]\frac{c^2}{\rho^2}u \)
Non riesco a capire quest'ultima uguaglianza! Spero che qualcuno di voi possa aiutarmi, grazie anticipatamente
Risposte
\(\displaystyle sen(dθ) \) è stato approssimato a \(\displaystyle dθ \) mediante l'uso della formula di taylor al primo ordine?
Sì.
Un moto centrale è determinato in maniera univoca dall'orbita ρ(θ) e dalla costanza della velocità areolare.
Questo è un po' fuorviante. In generale le orbite non sono chiuse, nel senso che ρ(θ) non è una funzione periodica, e quindi non si può scrivere come funzione di $\theta \in \mathds{S}^1$. Se si intende in senso lato $\theta \in \mathds{R}$ allora è corretto.
Riguardo alle formule successive, devo presumere che c sia una costante data da: $c = \frac{L}{m} = 2A'$ (L è il momento angolare.) Inoltre presumo $u = e_r$ e $u_t = e_{\theta}$. Allora quello che vuole dire credo sia:
\[ x = \rho e_\rho \]
e derivando:
\[ v = \dot{x} = \dot{\rho} e_\rho + \rho \dot{e_\rho} \]
e notando che $\rho$ è funzione solo di $\theta$ e ricordando che $\dot{e_\rho} = \dot{\theta} e_\theta $ ottieni la prima delle sue eguaglianze:
\[ v = \frac{\mathrm{d}\rho}{\mathrm{d}\theta} \dot{\theta} e_\rho + \rho \dot{\theta} e_\theta \]
Ora se calcoli $-\frac{d}{d\theta} (\frac{c}{\rho})$ e usi la sostituzione $\dot{\theta} = \frac{c}{\rho^2}$ ottieni il passaggio successivo. E da qui vai avanti derivando.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo