[SdM]- Distanza di equilibrio tra nuclei.

[BRN1]

Ciao a tutti, avrei da chiedervi un chiarimento riguardo un esercizio risolto che ho tra le mani.

ES.
La figura rappresenta lo spettro di assorbimento infrarosso di HBr gassoso. A partire dai dati sperimentali, determinare la distanza di equilibrio tra i nuclei di H e Br.


Svolgimento:
Siamo in approssimazione adiabatica vale. $E_(vib)$ può essere stimata dal grafico in modo approssimativo nel modo seguente:
Tra le energie di $0.31 eV$ e $0.32 eV$ sono presenti 4 picchi più il mancante relativo all'en. puramente vibrazionale, pertanto è possibile considerare circa 5 step. Pertanto:

$ DeltaE_(vib)=(0.32-0.31)/5=2*10^(-3) eV $ ogni step

nell'intervallo in esame, Il picco puramente vibrazionale si trova al quarto posto e pertanto si considerano 3 step:

$E_(vib)=0.31+3*2*10^(-3)=0.316 eV$

Fino a qui è tutto ok. Quello che non capisco è il passaggio successivo:
Si calcola la distanza di equilibrio tra i nuclei H e Br conscendo la distanza in energia tra due picchi rotazionali adiacenti e ricavando $I$ a partire dall'equazione:

$DeltaE_(rot)=(h-^2)/I=(2*10^(-3)+0.316)+(4*10^(-3)+0.316)$ con l'accortezza di passare da $eV$ a $J$

segue: $I=(h-^2)/(DeltaE_(rot))=3.4706*10^(-47) kg m^2$

$(h-^2)$ sarebbe l'acca tagliato al quadrato.

Domanda: ma per quale motivo $DeltaE_(rot)=(2*10^(-3)+0.316)+(4*10^(-3)+0.316)$? o più in generale: come faccio a dedurre dal grafico $DeltaE_(rot)$?

Grazie a chi mi aiuta!

.BRN

[Scotti1]

"BRN":Svolgimento:
Siamo in approssimazione adiabatica vale. $E_(vib)$ può essere stimata dal grafico in modo approssimativo nel modo seguente:
Tra le energie di $0.31 eV$ e $0.32 eV$ sono presenti 4 picchi più il mancante relativo all'en. puramente vibrazionale, pertanto è possibile considerare circa 5 step. Pertanto:

$ DeltaE_(vib)=(0.32-0.31)/5=2*10^(-3) eV $ ogni step

nell'intervallo in esame, Il picco puramente vibrazionale si trova al quarto posto e pertanto si considerano 3 step:

$E_(vib)=0.31+3*2*10^(-3)=0.316 eV$

Fino a qui è tutto ok.

Ciao BRN

non mi sono chiari i tuoi passaggi. Qui tu stai facendo un po' di confusione tra stati vibrazionali e rotazionali, tra $E$ e $Delta E$.
Innanzitutto l'energia totale rotovibrazionale della tua molecola è data da:

$E = E_(vib) +E_(rot) = (v +1/2)h_t omega_0 +(h_t^2)/(2I)l(l+1)$

dove $h_t$ è h tagliato, $v$ ed $l$ e numeri quantici vibrazionali e rotazionali.
A questo punto si vede facilmente che tutti i livelli vibrazionali consecutivi sono spaziati in egual misura di $h_t omega_0$.
I salti energetici avvengono tra due livelli rotazionali appartenenti a due livelli vibrazionali differenti, quindi se consideriamo due livelli vibrazionali consecutivi si ha:

$Delta E = Delta E_(vib) +Delta E_(rot) = h_t omega_0 +(h_t^2)/(I)(l+1)$

Quindi la riga corrispondente ad $h_t omega_0$, che dovrebbe essere presente a $0,316 eV$, manca in quanto il salto rotazionale tra livelli con stesso numero quantico rotazionale ( $l_1=l_2 rArr Delta l=0$) è proibito.
Fino a qui tutto chiaro ?

"BRN":
Domanda: ma per quale motivo $ DeltaE_(rot)=(2*10^(-3)+0.316)+(4*10^(-3)+0.316) $? o più in generale: come faccio a dedurre dal grafico $ DeltaE_(rot) $?

Grazie a chi mi aiuta!
.BRN

Ora prova a correggere il tuo risultato.

Bye

[BRN1]

Grazie Scotti per l'interessamento.

I passaggi che ho riportato non sono miei, ma quelli che trovo nella risoluzione data con l'esercizio.

"Scotti":
Innanzitutto l'energia totale rotovibrazionale della tua molecola è data da:

$E = E_(vib) +E_(rot) = (v +1/2)h_t omega_0 +(h_t^2)/(2I)l(l+1)$

dove $h_t$ è h tagliato, $v$ ed $l$ e numeri quantici vibrazionali e rotazionali.
A questo punto si vede facilmente che tutti i livelli vibrazionali consecutivi sono spaziati in egual misura di $h_t omega_0$.
I salti energetici avvengono tra due livelli rotazionali appartenenti a due livelli vibrazionali differenti, quindi se consideriamo due livelli vibrazionali consecutivi si ha:

$Delta E = Delta E_(vib) +Delta E_(rot) = h_t omega_0 +(h_t^2)/(I)(l+1)$

Quindi la riga corrispondente ad $h_t omega_0$, che dovrebbe essere presente a $0,316 eV$, manca in quanto il salto rotazionale tra livelli con stesso numero quantico rotazionale ( $l_1=l_2 rArr Delta l=0$) è proibito.
Fino a qui tutto chiaro ?
e

Fino a qui sì, ma quello che non capisco è proprio questo passaggio:
$ DeltaE_(rot)=(h_t^2)/I=(2*10^(-3)+0.316)+(4*10^(-3)+0.316) $
Perchè $DeltaE_(rot)$ è uguale a quella roba???

[Scotti1]

Infatti quel passaggio è errato.
Devi considerare l'energia tra due picchi e quindi c'è un meno di mezzo, cioè:

$ DeltaE_(rot)=(h_t^2)/I=(4*10^(-3)+0.316)-(2*10^(-3)+0.316) =2*10^(-3) eV$

da cui ricavi $r_0$.

[BRN1]

Ok, quindi c'è un evidente errore nella soluzione dell'esercizio.
Però non mi è ancora chiara una cosa: perchè la differenza tra due energie vibrazionali mi stimano la differenza di energia rotazionale?

[Scotti1]

"BRN": perchè la differenza tra due energie vibrazionali mi stimano la differenza di energia rotazionale?

Questo è un problema di struttura della materia.
Chiariamo meglio.

In una molecola diatomica, per ogni stato elettronico eccitato e non, troviamo una gamma di stati energetici vibrazionali nucleari. Ognuno di questi si suddivide in una ulteriore gamma di stati energetici rotazionali.




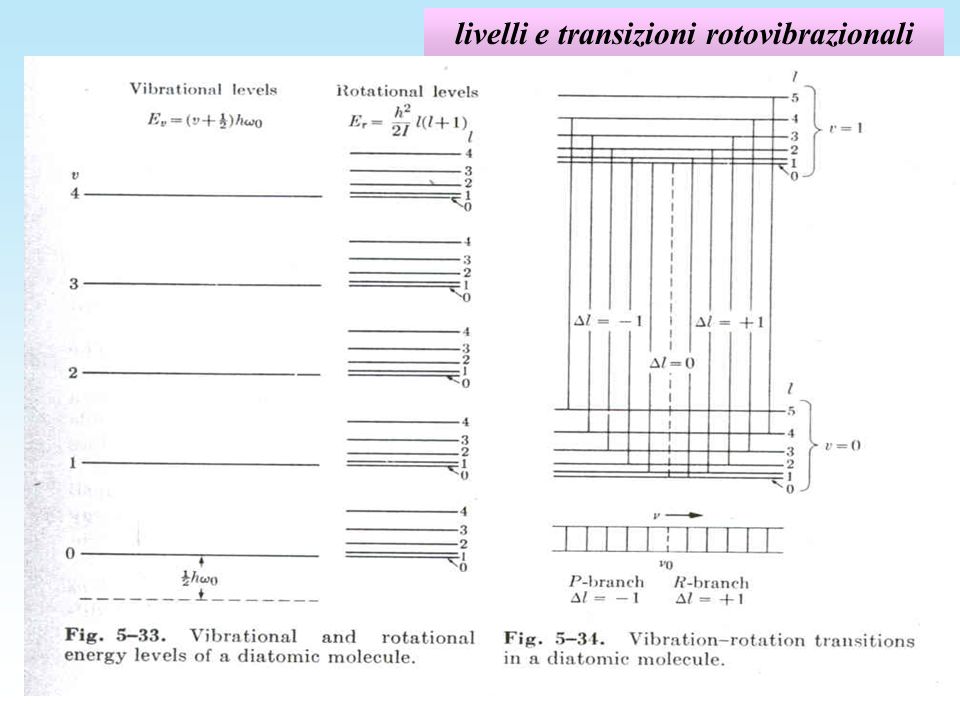
Le transizioni tra livelli energetici eccitati e non, avvengono secondo le regole di selezione quantistiche, ossia:

$Delta v =+-1$
$Delta l =+-1$

Ciò cosa significa: come vedi nella figura, ad ogni transizione vibrazionale (per es. tra $v=1$ a $v=0$) sarà associata una specifica transizione rotazionale (e quindi una specifica riga dello spettro: questo deve essere chiaro !!!)

$ Delta E = Delta E_(vib) +Delta E_(rot) = h_t omega_0 +(h_t^2)/(I)(l+1) $ (1)

Come vedi dalla (1) qualunque salto vibrazionale è distanziato di $h_t omega_0$ e quindi cadrà sempre nella stessa regione dello spettro indipendentemente dal valore di partenza di $v$, e questa energia nelle molecole diatomiche è tipicamente $approx 10^(-1) eV$ e cadono quindi nell'infrarosso.
Contemporaneamente la molecola si porterà su un livello energetico rotazionale diverso da quello di partenza secondo il
$Delta l =+-1$ e darà quindi un contributo energetico pari a

$Delta E_(rot) = (h_t^2)/(I)(l+1) $

che in questo caso invece dipende da $l$.

Quindi se ci fosse una transizione puramente vibrazionale avremmo una unica riga in $h_t omega_0$, ma con il contributo rotazionale le righe sono spaziate di

$ (h_t^2)/(I)$

Deve esserti chiaro che ogni riga dello spettro identifica un ben preciso salto energetico e non il valore assoluto dell'energia.
SSSSC

Bye

[BRN1]

Quindi uno spettro roto-vibrazionale rappresenta le linee spettrali di un unico salto vibrazionale. Ogni picco rappresenta un salto rotazionale permesso e le energie sulle ascisse sono quelle del relativo salto rotazionale. Dove manca il picco c'è la transizione puramente vibrazionale e pertanto in quel punto dell'ascissa l'energia è quella vibrazionale.

Scusa, non mi uccidere se ancora non ho capito, ma la teoria la sto studiando sulle dispense del mio docente e sono un vero disastro...

[Scotti1]

"BRN": Dove manca il picco c'è la transizione puramente vibrazionale e pertanto in quel punto dell'ascissa l'energia è quella vibrazionale.

Dove manca il picco non può esserci nessuna transizione ne rotazionale ne vibrazionale in quanto corrisponde ad un salto rotazionale proibito. Guarda il disegno postato.

Bye

[BRN1]

Però dove manca il picco ho $DeltaE=h_tw_0=DeltaE_(vib)$ cioè il salto vibrazionale.

Altra cosa, tutte quelle transizioni rotazionali mostrate nello spettro avvengono in contemporanea giusto?

[Scotti1]

"BRN":Però dove manca il picco ho $DeltaE=h_tw_0=DeltaE_(vib)$ cioè il salto vibrazionale.

Lo dici tu stesso: se manca il picco significa che non c'è emissione di fotone cioè di energia e quindi non c'è nessuna transizione.
Malgrado quel punto corrisponda al salto vibrazionale questo non avviene perché deve essere associato ad un salto rotazionale e quindi in questo caso l'energia emessa corrisponde proprio a quella delle righe spettrali.
Ripeto

Deve esserti chiaro che ogni riga dello spettro identifica un ben preciso salto energetico

Niente riga niente transizioni.

"BRN":
Altra cosa, tutte quelle transizioni rotazionali mostrate nello spettro avvengono in contemporanea giusto?

Le transizioni per un numero elevato di molecole avvengono in un tempo ragionevolmente piccolo e quindi praticamente in contemporanea.

Bye

[BRN1]

Ok, ora mi è tutto chiaro.

Grazie mille Scotti, soprattutto per la pazienza

Ciao!