Probalità $L_x$ in base di $L_z$

[ludwigZero]

Ciao.
Altro problema.
Ho questa funzione d'onda:

$\Psi = a* (Y_2^2 + Y_2^-2) + b * Y_0^0 - c * Y_2^0 + d * Y_1^0$

devo trovare la probabilità di $L_x$

io conosco $L_x$ in base $L_z$:

$h/sqrt(2) ((0,1,0),(-1,0,1),(0,-1,0))$

i cui autovalori sono: $0, h, -h$

ho: $l = 0$ con $m=0$
$l=1$ con $m=0$
$l=2$ con $m=0,-2,2$

io avevo pensato di far così:

$P(m=0) = (|b|^2 + |c|^2 + |d|^0)/(|a|^2 +|b|^2 + |c|^2 + |d|^2)$

$P(m=2 h) = P(m=-2 h) = |a|^2/(|a|^2 +|b|^2 + |c|^2 + |d|^2)$

ma non credo proprio che sia così

c'è un modo per scrivere la $\Psi$ in forma matriciale?

[hamilton2]

"ludwigZero":
io conosco $L_x$ in base $L_z$:

$h/sqrt(2) ((0,1,0),(-1,0,1),(0,-1,0))$

questo vale solo nel sottospazio $l=1$ (per il sottospazio $l$, hai matrici $(2l+1)\times(2l+1)$). Il tuo vettore di stato non è in nessun sottospazio di $l$ definito, è una combinazione lineare di $l$ diversi. Detto in un altro modo ancora, non è autovettore di $L^2$, dunque non puoi usare l'espressione di $L_x$ ristretta ad $l=1$.

$P(m=0) = (|b|^2 + |c|^2 + |d|^0)/(|a|^2 +|b|^2 + |c|^2 + |d|^2)$

$P(m=2 h) = P(m=-2 h) = |a|^2/(|a|^2 +|b|^2 + |c|^2 + |d|^2)$

queste sono le probabilità relative a $L_z$

Un modo di farlo è questo: calcoli le probabilità per i vari valori di $l$. Dopodiché, avendo scomposto la funzione d'onda come somma di autostati di $L^2$, per ognuno di questi calcoli la probabilità di $L_x$ usando le giuste matrici. Poi, la probabilità finale sarà data dalla somma delle probabilità pesate con le probabilità degli $l$.

cioè, scomponi così:

\(\displaystyle \Psi = \left( a (Y_2^2 + Y_2^{-2}) - c Y_2^0 \right) + (b Y_0^0) + (d Y_1^0) \)

questi tre termini sono autostati di $L^2$. Quindi le probabilità del numero quantico $l$ sono palesi (se le $Y$ sono normalizzate):

$P(l=0) = N |b|^2$
$P(l=1) = N|d|^2$
$P(l=2) = N(2|a|^2 + |c|^2)$

$N^{-1} := 2|a|^2+|c|^2 + |b|^2 + |d|^2$

Ora quello che facciamo è calcolare le probabilità di $m_x$ nei tre casi. Poi le moltiplichiamo per le $P(l)$ e le sommiamo. Insomma:

$P(m_x = n) = \sum_l P(l=m) \times P(m_x = n \text{ se }l=m )$

Partiamo dal caso $l=0$, ovvero prendiamo la funzione d'onda $bY_0^0$. Questa è facile, perché se $l=0$ allora tutte le componenti di $\vec L$ sono sempre nulle. Allora

$P_{l=0}(m_x=0) = 1$

Il caso $l=1$ è più interessante. La funzione d'onda è $dY_1^0$. $\vec L$ sono tre matrici $3\times 3$ in questo sottospazio. Scegliamo la rappresentazione standard, in cui ($\frac{h}{2\pi} = 1$ e fingi che $S$ sia $L$):



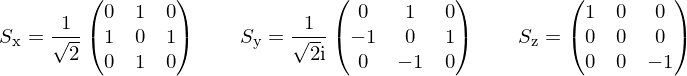
$d Y_1^0$ è per definizione l'autovettore di autovalore $0$ di $L_z$. Dunque è

$ ((0),(d),(0)) $

Ora diagonalizza $L_x$ (non stare a cercare gli autovalori, già li sai) e trova i due autovettori. Poi fai il prodotto scalare con il vettore sopra e fai il modulo quadro. Queste sono le probabilità relative a $m_x$ se lo stato fosse $d Y_1^0$.

Ora rifai la stessa cosa per la componente $l=2$, questa è più tosta, le matrici sono



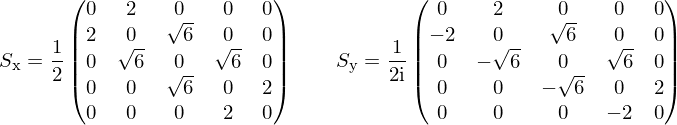
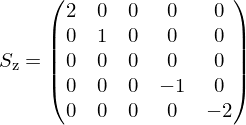
scrivi subito la componente $l=2$ della funzione d'onda, diagonalizzi $L_x$ e proietti lo stato sugli autovettori.

Finalmente puoi calcolare le probabilità totali.

Esiste anche un metodo algebrico che apparentemente è più veloce (Clebsh-Gordan) ma se guardi bene in realtà stai facendo bene o male la stessa fatica e non capisci. Quindi io tipicamente preferisco fare con le matrici.

[ludwigZero]

(farò i calcoli da te indicati con le matrici)

ma se fosse stato combinazione solo delle $l=1$ avrei potuto usare (**) applicandolo alla $\Psi$ ?

(**)

tipo:

$\Psi = a (Y_1^1 - Y_1^-1) + b Y_1^0$

$L_x \Psi = b h/sqrt(2) ( Y_1^1 + Y_1^-1) $

$ =0$
con:

$P(m=0)=0$
$P(m=1)=P(m=-1) = 1/2$

?

Suppongo di aver misurato $L_z$ nell stato $\Psi$ (questa del nuovo esempio...) e ho misurato $h$ domanda:


$<\Psi | Lz | \psi > = h$

l'autovettore relativo ad $h$ è $(a,0,0)$
per $L_x$ trovo l'autovettore relativo a (-h = quello che voglio trovare nel calcolo successivo) , prendo l'autovettore relativo a $-h$ (che se non è sbagliato è: $1/2 (1, -sqrt(2), 1) $ ne faccio il prodotto scalare con $(a,0,0)$ e poi modulo quadro per la probabilità?

grazie

[hamilton2]

"ludwigZero":
$ \Psi = a (Y_1^1 - Y_1^-1) + b Y_1^0 $
$ L_x \Psi = b h/sqrt(2) ( Y_1^1 + Y_1^-1) $

mi pare che questa sia sbagliata. Non mi sono chiare le considerazioni successive, ad esempio se $m$ è $m_z$ o $m_x$ e come ci arrivi.

"ludwigZero":
Suppongo di aver misurato $ L_z $ nell stato $ \Psi $ (questa del nuovo esempio...) e ho misurato $ h $ domanda:


$ <\Psi | Lz | \psi > = h $

questa ultima equazione è vera, ma non è equivalente al fatto che $| \psi \rangle$ è un autovettore, è più debole. Ti conviene scrivere, secondo me, $L_z | \psi \rangle = h | \psi \rangle$. Questa è un'affermazione più forte. Dal solo valore di aspettazione non puoi dedurre che è un autostato. Una banalità che bisogna ripetere, comunque

l'autovettore relativo ad $ h $ è $ (a,0,0) $
per $ L_x $ trovo l'autovettore relativo a (-h = quello che voglio trovare nel calcolo successivo) , prendo l'autovettore relativo a $ -h $ (che se non è sbagliato è: $ 1/2 (1, -sqrt(2), 1) $ ne faccio il prodotto scalare con $ (a,0,0) $ e poi modulo quadro per la probabilità?

yes, l'idea è giusta, ma ricordati di normalizzare tutto

[ludwigZero]

"ludwigZero":



tipo:

$\Psi = a (Y_1^1 - Y_1^-1) + b Y_1^0$

Ho applicato:

$L_+ Y_(l,m) = h sqrt(l(l+1) - m(m+1)) Y_(l,m+1)$

$L_- Y_(l,m) = h sqrt(l(l+1) - m(m-1)) Y_(l,m1)$

$L_x \Psi = b h (Y_1^1 + Y_1^-1)$

(ho rifatto meglio i conti, in effetti prima c'era $1/sqrt(2)$ di troppo)

$ = b^2 h^2 (1) + b^2 h^2 (-1) = 0$

"hamilton":
[quote="ludwigZero"]
conviene scrivere, secondo me, $ L_z | \psi \rangle = h | \psi \rangle $.

[/quote]

dato che:

$L_z |l,m \rangle = m h |l,m \rangle$

$ L_z | \psi \rangle = m h ( a (Y_1^1 - Y_1^-1) + b Y_1^0 ) = a h (Y_1^1 + Y_1^-1) $

cosa posso dedurre da:

$ L_z | \psi \rangle = h | \psi \rangle $ ?

come sarebbe con le matrici partendo da:

$Y_1^1 = ((1),(0),(0))$

$Y_1^1 = ((0),(0),(-1))$

$Y_1^0 = ((0),(0),(0))$

[hamilton2]

"ludwigZero":
$L_x \Psi = b h (Y_1^1 + Y_1^-1)$

qua ancora mancano dei termini

$Y_1^0 = ((0),(0),(0))$

questo è semplicemente impossibile, i vettori di stato non possono essere nulli

[ludwigZero]

Ho applicato:

$L_+ Y_(l,m) = h sqrt(l(l+1) - m(m+1)) Y_(l,m+1)$

$(L_-) Y_(l,m) = h sqrt(l(l+1) - m(m-1)) Y_(l,m-1)$

scrivo i conti:

$L_+ Y_1^1 = 0 $

$L_+ Y_1^-1 = h sqrt(2) Y_1^0$

$L_+ Y_1^0 = h sqrt(2) Y_1^1$

$ 1/sqrt(2) sqrt(2) { - a h Y_1^0 + b h Y_1^1 }$

$(L_- ) (Y_1^1) = h sqrt(2) Y_1^0$

$(L_- ) (Y_1^-1 ) = 0$

$(L_- ) (Y_1^0) = h sqrt(2) Y_1^-1$



$1/sqrt(2) sqrt(2) { a h Y_1^0 + b h Y_1^-1 }$

sommando le due viene che:

${ - a h Y_1^0 + b h Y_1^1 } + { a h Y_1^0 + b h Y_1^-1 } = b h (Y_1^1 + Y_1^-1 )$

dove sbaglio?

riguardo alle matrici, in base Lz sono:


$ | 1,1 \rangle = ((1),(0),(0))$

$ | 1,0 \rangle = ((0),(1),(0))$

$ | 1,-1 \rangle = ((0),(0),(1))$

quindi: $ L_z | \psi \rangle = h | \psi \rangle $.

viene così : $((a),(0),(a)) = ((a),(b),(a))$

quindi $b=0$

quindi un possibile autostato è: $((a),(0),(a))$ ?

[hamilton2]

"ludwigZero":
dove sbaglio?

da nessuna parte, è colpa mia, mi sono copiato la $\Psi$ con un segno sbagliato

riguardo alle matrici, in base Lz sono:

non so se questo è un errore di battitura o sostanziale. Quella che segue è la base, e messa insieme non forma $L_z$, ma l'identità. Mi sento di doverlo dire perché non mi è chiaro cosa fai dopo:

quindi: $ L_z | \psi \rangle = h | \psi \rangle $.

ma questo è semplicemente falso. O lo stai imponendo? O la $|\psi\rangle$ è una cosa diversa dalla $\Psi$? Se sì, perché?

viene così : $((a),(0),(a)) = ((a),(b),(a))$

quindi $b=0$

quindi un possibile autostato è: $((a),(0),(a))$ ?

non sono sicuro di quale sia la domanda per la quale questa dovrebbe essere la risposta. Comunque credo di no, non mi pare autostato né di $L_x$ né di $L_z$.

[ludwigZero]

io voglio rispondere a questa domanda:

"ludwigZero":
Suppongo di aver misurato $ L_z $ nell stato $ \Psi $ (questa del nuovo esempio...) e ho misurato $ h $ domanda:


$ <\Psi | Lz | \psi > = h $

Ti conviene scrivere, secondo me, $ L_z | \psi \rangle = h | \psi \rangle $.
[quote=ludwigZero]

voglio l'autostato relativo all'autovalore $h$

essendo:
$L_z = h ((1,0,0),(0,0,0),(0,0,-1))$

$h ((1,0,0),(0,0,0),(0,0,-1)) ((x),(y),(z)) = h ((x),(y),(z))$

viene un autovettore del tipo: $((x),(0),(0)) = x ((1),(0),(0))$

quindi sarebbe l'autostato associato a $| 1,1 \rangle $ moltiplicato per una costante (ch credo sia proprio $a$), ti trovi?

[hamilton2]

Ok. Allora:

metto $\frac{h}{2\pi} =1$, per capirci.

Lo stato iniziale è $| \psi \rangle = a(Y_1^1 - Y_1^{-1}) + b Y_1^0$.

Poi misuri $L_z$ e ottieni un valore $+1$.

Quindi lo stato è cambiato. Chiamiamolo $|\phi \rangle$. $|\phi\rangle$ è l'autostato di valore $+1$ di $L_z$ per i postulati della quantistica. Vale:

$L_z |\phi \rangle = +1 |\phi \rangle$

Questo significa che $|\phi \rangle = |1,1\rangle$. Dunque nella base formata da $|1,1\rangle$, $|1,0\rangle$, $|1,-1\rangle$, $|\phi \rangle$ si scrive (normalizzato)

$((1),(0),(0))$

che è quello che hai trovato tu, quindi dovremmo esserci.

Faccio una piccola precisazione: in conseguenza della misura dovremmo a rigore proiettare $|\psi \rangle$ sull'autospazio di $L_z$ relativo a $+1$. Mapperò, questo autospazio ha dimensione uno. Dunque, a meno che $|\psi \rangle$ non fosse ortogonale a tale autospazio (e non lo era, altrimenti la misura era impossibile), la proiezione sarà necessariamente $a|1,1\rangle$, che a meno di normalizzazione (che non è fisica), non dipende da $|\psi \rangle$. Questa è una proprietà di operatori autoaggiunti come $L_z$, che è la completezza, che ti dice che in conseguenza di una misura di un tale operatore, tu conosci completamente lo stato del sistema, indipendentemente da ciò che è successo prima. Vorrei enfatizzare che questo vale se gli autospazi dell'operatore che misuri sono di dimensione 1.

Nota bene del nota bene: $L_z$ è completo solo nel sottospazio $l=1$.

Questo è per dire, in soldoni, che puoi buttare via $|\psi\rangle$. L'informazione data da $|\psi\rangle$ è stata cancellata nella misura.

Ora hai scritto $|\phi \rangle$ in una base conveniente in cui $L_z$ è diagonale e $L_x$ lo conosci. Inoltre $|\phi\rangle$ è normalizzato. Allora la tua soluzione, la tua probabilità, è il modulo quadro della proiezione di $|\phi \rangle$ sull'autospazio di $L_x$ relativo a $-1$. Scrivo in lingua universale:

$P = \frac{ |\langle \phi | -1 \rangle|^2 }{ \langle\phi|\phi\rangle \langle -1 | -1 \rangle } $

Dove $|-1 \rangle$ è un vettore dell'autospazio suddetto. Chiaramente se hai normalizzato sia $|\phi\rangle$ che $|-1\rangle$ il denominatore fa $1$ e non ti serve.

Dunque ti basta la rappresentazione di $|-1 \rangle$ come vettore colonna nella base di autovettori di $L_z$. Dunque prendi la matrice per $L_x$ e la diagonalizzi.

[ludwigZero]

grazie per l'attenta spiegazione sulla completezza di $L_z$

l'autovettore associato a $-h$ è $(1,-sqrt(2),1)$ la normalizzo e viene: $1/2 (1,-sqrt(2),1)$


$1/2 (1,0,0)*(1,-sqrt(2),1) = 1/2$ $P(-h) = 1/4$


mi potrebbe chiedere di nuovo una probabilità, dopo una misura di $L_x $, di $L_y$ ?

cioè una richieste di probabilità misura in misura?
giusto?