Moto di rotazione+traslazione
Ciao a tutti, avrei bisogno del vostro aiuto per risolvere questo esercizio:
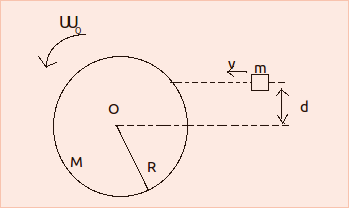
Una moneta omogenea di massa m e raggio R posta in posizione verticale su un piano orizzontale viene messa in moto con velocità iniziale v[size=59]0[/size]. Alla moneta viene inoltre impartito un moto rotatorio attorno al suo asse con velocità angolare iniziale ω[size=59]0[/size], con verso di rotazione opposto a quello che si avrebbe se la moneta rotolasse senza strisciare. Il coefficiente di attrito dinamico tra moneta e tavolo è μ. Calcolare:
-La velocità angolare iniziale necessaria per far sì che il moto traslatorio e quello rotazionale cessino simultaneamente.
-In corrispondenza di ω[size=59]0[/size] la distanza percorsa fino all'arresto.
-L'aumento di temperatura della moneta, ammettendo che metà dell'energia cinetica dissipata a causa dell'attrito si sia riversata nella moneta sotto forma di calore (si assuma che il calore specifico sia c).
Grazie anticipatamente a tutti quelli che risponderanno.
Una moneta omogenea di massa m e raggio R posta in posizione verticale su un piano orizzontale viene messa in moto con velocità iniziale v[size=59]0[/size]. Alla moneta viene inoltre impartito un moto rotatorio attorno al suo asse con velocità angolare iniziale ω[size=59]0[/size], con verso di rotazione opposto a quello che si avrebbe se la moneta rotolasse senza strisciare. Il coefficiente di attrito dinamico tra moneta e tavolo è μ. Calcolare:
-La velocità angolare iniziale necessaria per far sì che il moto traslatorio e quello rotazionale cessino simultaneamente.
-In corrispondenza di ω[size=59]0[/size] la distanza percorsa fino all'arresto.
-L'aumento di temperatura della moneta, ammettendo che metà dell'energia cinetica dissipata a causa dell'attrito si sia riversata nella moneta sotto forma di calore (si assuma che il calore specifico sia c).

Grazie anticipatamente a tutti quelli che risponderanno.
Risposte
dovresti gentilmente mostrarci come faresti cosi' capiamo cosa non hai capio.Grazie
beh, il mio problema sta proprio all'inizio... non capisco come interpretare il problema: inizialmente pensavo di trattare la rotazione del corpo come puro rotolamento separatamente dalla traslazione, ma da quello che ha detto la professoressa non credo sia corretto, inoltre dal disegno (che era allegato al problema, non l'ho fatto io) sembrerebbe che il moto di rotazione sia nel verso contrario rispetto alla traslazione e questo mi porta a pensare che per risolvere il primo punto dovrei eguagliare il moto rotatorio e quello traslatorio ma non sono del tutto sicura, quel "con verso di rotazione opposto a quello che si avrebbe se la moneta rotolasse senza strisciare" mi confonde un po'...
Il moto e' di rotolamento con strisciamento.La forza di attrito dinamico in questo caso e' dissipativa e il suo verso e' opposto al moto del centro di massa.Non solo ma il momento dell'attrito contrasta la rotazione iniziale della moneta.detto questo fatti l'equazione dei momenti e la seconda legge di Newton e risolvi il problema.
Mi associo al problema di ladidely, e vorrei chiedere: il problema può essere risolto utilizzando il formalismo lagrangiano?[/tex]
Grazie legendre, ho provato a risolverlo:

è questo lo svolgimento giusto o ci sono errori?

è questo lo svolgimento giusto o ci sono errori?
Perche' sommi forza attrito e forza peso ?
non devo considerare la forza peso tra quelle agenti sul corpo?
non vorrei essere insistente, ma nessuno sa dirmi se ho svolto l'esercizio in maniera corretta?
è un esercizio importante che devo assolutamente risolvere...
è un esercizio importante che devo assolutamente risolvere...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo