Moto circolare in una conca
$ f = -0.581 J $Ciao a tutti, ho un dubbio sul seguente esercizio. Vorrei sapere se ho svolto correttamente
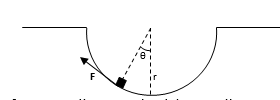
Un corpo di 0.2 kg si trova in una conca di raggio pari a 0.5 metri.
Il corpo parte da fermo in posizione 90 gradi. Quando passa dal punto piu in basso ha velocita pari a 2 metri al secondo.
a)Si calcoli il lavoro svolto dalla forza F tangente alla conca che si deve applicare affinché valga quanto detto sopra.
Inizialmente avevo iniziato calcolando l'accelerazione con cui si muove il corpo e poi applicare la seconda legge di Newton. Poi ho pensato che forse la strada più veloce è quella di applicare la conservazione dell'energia meccanica.
E' corretto dire che quando il corpo passa dal punto più basso, tutta l'energia potenziale si è convertita in energia cinetica a meno del lavoro svolto da F?
quindi l'energia cinetica finale è $K = 1/2 mv^2 = 0.4 J$ mentre l'energia potenziale iniziale $mgh = mgR(1-cos(90)) = 0.981 J$ e quindi $F = -0.581 J$?
b) Si calcoli il modulo della reazione R sviluppata dalla conca nel punto piu basso
Qui invece considero che il corpo è soggetto a $R, F_centripet, F_peso$ e applico il II principio?
Un corpo di 0.2 kg si trova in una conca di raggio pari a 0.5 metri.
Il corpo parte da fermo in posizione 90 gradi. Quando passa dal punto piu in basso ha velocita pari a 2 metri al secondo.
a)Si calcoli il lavoro svolto dalla forza F tangente alla conca che si deve applicare affinché valga quanto detto sopra.

Inizialmente avevo iniziato calcolando l'accelerazione con cui si muove il corpo e poi applicare la seconda legge di Newton. Poi ho pensato che forse la strada più veloce è quella di applicare la conservazione dell'energia meccanica.
E' corretto dire che quando il corpo passa dal punto più basso, tutta l'energia potenziale si è convertita in energia cinetica a meno del lavoro svolto da F?
quindi l'energia cinetica finale è $K = 1/2 mv^2 = 0.4 J$ mentre l'energia potenziale iniziale $mgh = mgR(1-cos(90)) = 0.981 J$ e quindi $F = -0.581 J$?
b) Si calcoli il modulo della reazione R sviluppata dalla conca nel punto piu basso
Qui invece considero che il corpo è soggetto a $R, F_centripet, F_peso$ e applico il II principio?
Risposte
Se la conca è vincolata ovvero tenuta fissa:
a) Si
b) Si
Nota: non ho verificato i conti
a) Si
b) Si
Nota: non ho verificato i conti
Tieni presente che la reazione della conca (meno il peso) È la forza centripeta, ci sono DUE forze, non tre
Grazie mille ad entrambi. Se invece avessi voluto risolvere il primo quesito senza applicare la conservazione dell'energia meccanica, come avrei dovuto fare? C'è un altro modo? (anche se più lungo, per esercitarmi)
Si tratta di un moto puntiforme su una linea curva, per cui basta proiettare sulla linea le forze e scrivere l'equazione del moto in termini di spostamento sulla curva stessa. Quindi:
$m*(d^2 s)/dt^2 = - m*g sin(theta) + F$
ove $s=r*theta$ avendo definito lo spostamento a salire in direzione dell'aumento di $theta$ e quindi ancora:
$m*r (d^2 theta)/dt^2 = - m*g sin(theta) + F$
con $theta(0) = pi/2$ e $(d theta) / (dt) (0) = 0$
Questa è l'equazione del moto, ma purtroppo è un'equazione differenziale non lineare, che può essere risolta solo con metodi numerici. Tuttavia con qualche manipolazione si può integrare questa equazione per ottenere quello che si chiama un integrale primo, che altro non rappresenta che la conservazione dell'energia meccanica.
$m*(d^2 s)/dt^2 = - m*g sin(theta) + F$
ove $s=r*theta$ avendo definito lo spostamento a salire in direzione dell'aumento di $theta$ e quindi ancora:
$m*r (d^2 theta)/dt^2 = - m*g sin(theta) + F$
con $theta(0) = pi/2$ e $(d theta) / (dt) (0) = 0$
Questa è l'equazione del moto, ma purtroppo è un'equazione differenziale non lineare, che può essere risolta solo con metodi numerici. Tuttavia con qualche manipolazione si può integrare questa equazione per ottenere quello che si chiama un integrale primo, che altro non rappresenta che la conservazione dell'energia meccanica.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo