Momento Risultante per Forze Convergenti: Sempre Null?

[Bacchinif]

Salve a tutti, vi pongo un quesito di carattere grafico.
Sul mio manuale di testo è scritto che se delle forze convergenti in un punto A sono applicate ad un corpo, allora il Momento Risultante di queste forze sarà certamente nullo. Del resto è intuitivo che tutti i singoli Momenti saranno nulli, in quanto la distanza tra braccio della forza e punto di applicazione è pari a zero.

Ma se prendessi un altro punto?
Graficamente si vede che le distanze (non quelle in verdi, ma possiamo facilmente immaginarcele) faranno sì che si abbiano prodotti vettoriali non nulli singolarmente.

Allora il Momento Risultante è in ogni caso nullo, indipendentemente dalla scelta del punto?



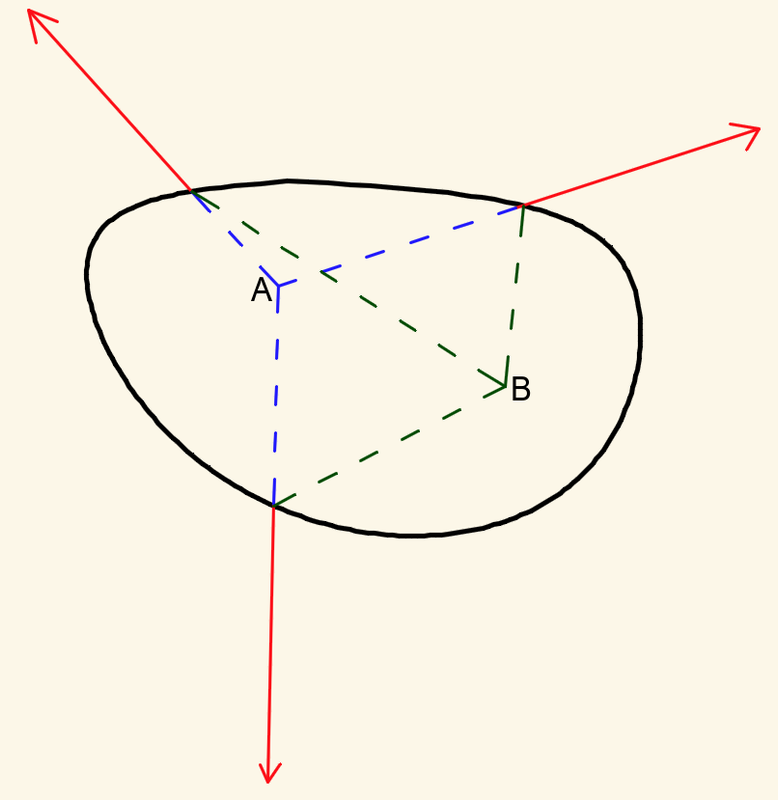
Scusate, ma l'ultima forza a destra è venuta tagliata. Poco cambia se ce la immaginiamo più corta.

[Shackle]

In generale, non è vero quanto affermato dal tuo libro. E lo vedi tu stesso, dal disegno che hai fatto e dal dubbio che ti è venuto.
Limitiamoci, per semplicità , a considerare un sistema piano di forze , e prendiamone solo due, $vecF_1$ e $vecF_2$ , che non siano parallele. Se non sono parallele, le loro rette di azione, giacenti nel comune piano, si incontrano in un punto. Trasporta le due forze in questo punto , fanne la somma vettoriale ( il parallelogramma delle forze) , e disegna la risultante : $vecR =vecF_1 + vecF_2$ . La risultante ha una sua retta di azione, che giace ancora sul piano naturalmente.
Il momento totale delle due forze date è nullo solo rispetto a un polo preso sulla retta di azione di $vecR$ . MA se prendi un polo non giacente su tale retta, il momento del sistema di forze rispetto a questo polo non è nullo.

Nello spazio, il problema è più complicato.