Momento d'inerzia
ciao a tutti! qualcuno mi sa dire in che modo posso calcolare il momento d'inerzia di un disco che ruota sul suo diametro? considerando che il disco che devo usare non ha spessore infinitesimo immagino possa essere assimilabile ad un cilindro, ma comunque non so come fare.
Risposte
sulla wiki c'è questo risultato
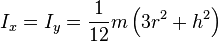
ove r è il raggio e h l'altezza del disco (omogeneo)
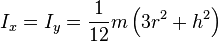
ove r è il raggio e h l'altezza del disco (omogeneo)
se dice che ruota intorno ad un diametro, supponga che si possa considerare, se non di spessore infinitesimo, almeno di uno spessore costante piccolo rispetto al raggio. il momento d'inerzia ti risulta che a livello elementare tu lo possa scrivere come una sommatoria di tante piccole masse moltiplicate per il quadrato della distanza dall'asse di rotazione? ebbene, se l'asse di rotazione è un diametro, le parti del disco che si possono considerare a distanza "costante" dal diametro sono striscioline parallele. se chiamo r la distanza di una strisciolina del disco dal diametro di rotazione, se R è il raggio del disco, con il teorema di Pitagora trovo la lunghezza della strisciolina: $sqtr(R^2-r^2)$ che, moltiplicata per la densità (che immaginiamo sia costante = delta) ed anche per un eventuale fattore "piccolo" h che potrebbe indicare lo spessore del disco, moltiplicata soprattutto per dr che rappresenta la larghezza infinitesima della strisciolina, ci dà la massa infinitesima che anremo ad integrare moltiplicandola ulteriormente per il quadrato della distanza (che è sempre r). in formule:
integrale (da 0 a R) di $h*delta*sqrt(R^2-r^2)*r^2*dr$ rappresenta il momento d'inerzia relativo ad una metà del disco: va moltiplicato per 2. con un po' d'impegno, l'integrale si fa. ciao.
integrale (da 0 a R) di $h*delta*sqrt(R^2-r^2)*r^2*dr$ rappresenta il momento d'inerzia relativo ad una metà del disco: va moltiplicato per 2. con un po' d'impegno, l'integrale si fa. ciao.
Scusate ma il calcolo mi sembra molto più semplice.
Consideriamo un sistema di riferimento con origine nel centro del disco (sottile) di raggio $R$ e massa $m$ (uniformemente distribuita) con l'asse $z$ normale al piano del disco.
Penso che tutti sappiamo che:
$I_z = 1/2 mR^2$
(la dimostrazione è comunque un semplice integrale in coordinate polari).
Ora, dato che:
$r^2 = x^2+y^2$
si ha:
$I_z = I_x+I_y$
e inoltre per simmetria:
$I_x = I_y$
si ottiene quindi:
$I_x = 1/4 mR^2$
Consideriamo un sistema di riferimento con origine nel centro del disco (sottile) di raggio $R$ e massa $m$ (uniformemente distribuita) con l'asse $z$ normale al piano del disco.
Penso che tutti sappiamo che:
$I_z = 1/2 mR^2$
(la dimostrazione è comunque un semplice integrale in coordinate polari).
Ora, dato che:
$r^2 = x^2+y^2$
si ha:
$I_z = I_x+I_y$
e inoltre per simmetria:
$I_x = I_y$
si ottiene quindi:
$I_x = 1/4 mR^2$
..... soluzione che coincide con quella di Wedge per $h$<<$R$
ci deve essere qualche baco nel sito perché non riesco a editare il mio messaggio ... prima me lo apre e poi mi dice che non è mio
ci deve essere qualche baco nel sito perché non riesco a editare il mio messaggio ... prima me lo apre e poi mi dice che non è mio
ops ... mi era sfuggito il 'non' infinitesimo ...
in ogni caso considerando una striscia sottile di spessore $dz$ e massa $dm$ per un disco spesso è:
$dI_z=1/4 R^2 dm +z^2 dm=1/4 R^2 dm +(m/h)z^2 dz$
che integrata tra $-h/2 e h/2$ fornisce la formula indicata da Wedge:
$I_z=1/4mR^2+1/12mh^2$
in ogni caso considerando una striscia sottile di spessore $dz$ e massa $dm$ per un disco spesso è:
$dI_z=1/4 R^2 dm +z^2 dm=1/4 R^2 dm +(m/h)z^2 dz$
che integrata tra $-h/2 e h/2$ fornisce la formula indicata da Wedge:
$I_z=1/4mR^2+1/12mh^2$
"mircoFN":
Scusate ma il calcolo mi sembra molto più semplice.
Consideriamo un sistema di riferimento con origine nel centro del disco (sottile) di raggio $R$ e massa $m$ (uniformemente distribuita) con l'asse $z$ normale al piano del disco.
Penso che tutti sappiamo che:
$I_z = 1/2 mR^2$
(la dimostrazione è comunque un semplice integrale in coordinate polari).
Ora, dato che:
$r^2 = x^2+y^2$
si ha:
$I_z = I_x+I_y$
e inoltre per simmetria:
$I_x = I_y$
si ottiene quindi:
$I_x = 1/4 mR^2$
Da quello che ho capito io il disco non è sottile ma ha una altezza h per cui la formula corretta è quella di Wedge.
grazie, sul mio libro non c'era scritto nulla di tutto ciò. ora tutto ha un po' più di senso.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo