Modulo e direzione del vettore risultante

[75america]

Tre vettori sono orientati come in figura, con a=20 unità, b=40 unità e c=30 unità. Si trovino le componenti x e y il modulo e la direzione del vettore risultante



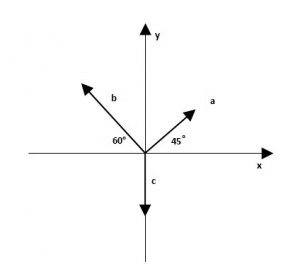
Le componenti x e y riesco a trovarle:

$\{(a_x=acos45°),(b_x=bcos60°):}$

$\{(a_x=acos45°),(b_y=bsen60°):}$

$\{(c_x=0),(c_y=-30):}$

$\{(R_x=acos45°+bcos60°+0),(a_y=asen45°+bsen60°-30):}$

$\{(R_x=14.2+20=34.2 unità),(a_y=14.2+34.8-30=19 unità):}$

Non so se ho fatto bene per il modulo dovrei fare $sqrt(R_x^2+R_y^2)$? e la direzione come la ottengo?

[Summerwind78]

Ciao

una volta che hai ottenuto $R_x$ e $R_y$ ti trovi l'angolo $\varphi$ facendo

$varphi = arctan(R_y/R_x)$ se $R_x>0$
altrimenti

$varphi = arctan(R_y/R_x) + pi$ se $R_x<0$

[75america]

ok, viene fuori $0,502 rad (28°)$, ma rispetto al primo quadrante o quale quadrante perchè per esempio l'angolo di b è $60°$ gradi ma nel secondo quadrante, quindi come farei a stabilirlo?
Grazie mille

[Summerwind78]

Sarebbe riferito al primo quadrante ma devi vedere l'angolo di $b$ sempre rispetto al primo quadrante

quindi come $180-60 = 120°$


Io ti consiglierei di considerare tutti gli angoli del tuo esercizio riferendoti al primo quadrante in modo da non fare confusione con segni