Masse su un piano e carrucole
Un corpo di massa $m_A=2kg$ è posto su un piano orizzonatale liscio. Esso è collegato tramite due fili a due corpi di massa $m_B=4kg$ e $m_C=1kg$. Inizialmente il sistema è in quiete. Calcolare A)l'accelerazione del sistema b)la Tensione dei due fili
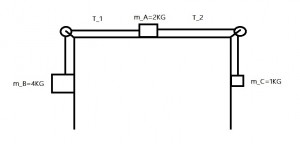
Io il problema l'ho risolto, impostando il verso positivo da destra verso sinistra, si può fare così o dovrei sempre considerarlo da sinistra verso destra(dati gli assi cartesiani)
Diagramma forze:
$\{(m_Bg-T_1=m_B*a), (T_1-T_2=m_A*a), (T_2-m_Cg=m_C*a):}$
$m_Bg-m_Cg=(m_B+m_A+m_C)*a=4.2m/s^2$
$4*9.8-T1=4*4.2=>T_1=39.2-16.8=22.4N$
$22.4-T_2=8.4=>T_2=14N$
Se avessi considertao il verso positivo da sinistra verso destra come avrei dovuto scrivere il diagramma delle forze, come avrei dovuto considerare le $m_Aa$ e $m_Ca$ positive o negative, è lì che m'imbroglio, perciò ho scelto da destra verso sinistra

Io il problema l'ho risolto, impostando il verso positivo da destra verso sinistra, si può fare così o dovrei sempre considerarlo da sinistra verso destra(dati gli assi cartesiani)
Diagramma forze:
$\{(m_Bg-T_1=m_B*a), (T_1-T_2=m_A*a), (T_2-m_Cg=m_C*a):}$
$m_Bg-m_Cg=(m_B+m_A+m_C)*a=4.2m/s^2$
$4*9.8-T1=4*4.2=>T_1=39.2-16.8=22.4N$
$22.4-T_2=8.4=>T_2=14N$
Se avessi considertao il verso positivo da sinistra verso destra come avrei dovuto scrivere il diagramma delle forze, come avrei dovuto considerare le $m_Aa$ e $m_Ca$ positive o negative, è lì che m'imbroglio, perciò ho scelto da destra verso sinistra
Risposte
Se guardi bene le equazioni che hai scritto, ti rendi conto che sia per le accelerazioni che per le forze hai indicato col simbolo (ad es. con $T_1$ e con $a$) il "modulo" dei rispettivi vettori.
Il segno da mettere nelle equazioni lo hai stabilito in base al verso da te assunto per gli assi, e in base a quello che ti aspetti sia il movimento del sistema, giusto?
Se metti l'asse orizzontale positivo verso destra, e dai ai simboli sempre il significato di "modulo" , devi cambiare dei segni nelle equazioni, non solo davanti ad $a$ ma pure davanti a qualche tensione.
Il segno da mettere nelle equazioni lo hai stabilito in base al verso da te assunto per gli assi, e in base a quello che ti aspetti sia il movimento del sistema, giusto?
Se metti l'asse orizzontale positivo verso destra, e dai ai simboli sempre il significato di "modulo" , devi cambiare dei segni nelle equazioni, non solo davanti ad $a$ ma pure davanti a qualche tensione.
Allora se io impostassi il verso positivo da sinistra verso destra:
$\{(-m_bg+T_1=-m_ba),(-T_1+T_2=m_Aa),(-T_2+m_Cg=m_Ca):}$
allora io credo di aver sbagliato i segni di tutti i secondi membri delle equazioni(cioè i segni delle accelerazioni, come li dovrei scrivere?)), perchè i corpi scendono tutti i sinistra quindi dovrebbero essere negative tutte considerando il verso pos. da sinistra a destra..
fammi capire, grazie
$\{(-m_bg+T_1=-m_ba),(-T_1+T_2=m_Aa),(-T_2+m_Cg=m_Ca):}$
allora io credo di aver sbagliato i segni di tutti i secondi membri delle equazioni(cioè i segni delle accelerazioni, come li dovrei scrivere?)), perchè i corpi scendono tutti i sinistra quindi dovrebbero essere negative tutte considerando il verso pos. da sinistra a destra..
fammi capire, grazie
LA miglior cosa, in questi casi(ni), è scrivere le equazioni in forma vettoriale.
Assumi :
-asse $y$ orientato positivo verso l'alto ( col suo versore $\vecj$)
-asse $x$ orientato positivo verso destra (col suo versore $\veci$ )
-le tre masse hanno la stessa accelerazione scalare, cioè di modulo $a$.
-l'accelerazione vettoriale della massa $m_b$ sarà orientata verso il basso, in verso opposto a $\vecj$, cioè sarà :
$\veca_b = -a*\vecj$
-l'accelerazione vettoriale della massa $m_a$ è diretta in verso opposto a $\veci$ , cioè sarà : $\veca_a = -a\veci$
-l'accelerazine vettoriale della massa $m_c$ è diretta nello stesso verso di $\vecj$, cioè sarà : $\veca_c = a\vecj$
Le tre equazioni del moto in forma vettoriale si scrivono :
1) $m_b*\veca_b = -m_ba\vecj = - m_bg\vecj +T_1\vecj$
2) $m_a*\veca_a = -m_aa\veci = -T_1\veci + T_2\veci$
3) $m_c*\veca_c = m_c a\vecj = -m_cg\vecj + T_2\vecj$
Ora devi solo proiettare sugli assi $x$ ed $y$, moltiplicando scalarmente per i rispettivi versori.
e infatti, così facendo, e pi cambiando dei segni e sommando membro a membro , risulta :
$(m_a +m_b +m_c) *a = (m_b - m_c) * g $
da cu s ricava $a$ .
Questa eq. si poteva scrivere subito :
Forza motrice $m_b*g$ meno forza resistente $m_c*g$ uguale massa totale x accelerazione $a$ . Le tensioni sono forze interne al sistema.
Assumi :
-asse $y$ orientato positivo verso l'alto ( col suo versore $\vecj$)
-asse $x$ orientato positivo verso destra (col suo versore $\veci$ )
-le tre masse hanno la stessa accelerazione scalare, cioè di modulo $a$.
-l'accelerazione vettoriale della massa $m_b$ sarà orientata verso il basso, in verso opposto a $\vecj$, cioè sarà :
$\veca_b = -a*\vecj$
-l'accelerazione vettoriale della massa $m_a$ è diretta in verso opposto a $\veci$ , cioè sarà : $\veca_a = -a\veci$
-l'accelerazine vettoriale della massa $m_c$ è diretta nello stesso verso di $\vecj$, cioè sarà : $\veca_c = a\vecj$
Le tre equazioni del moto in forma vettoriale si scrivono :
1) $m_b*\veca_b = -m_ba\vecj = - m_bg\vecj +T_1\vecj$
2) $m_a*\veca_a = -m_aa\veci = -T_1\veci + T_2\veci$
3) $m_c*\veca_c = m_c a\vecj = -m_cg\vecj + T_2\vecj$
Ora devi solo proiettare sugli assi $x$ ed $y$, moltiplicando scalarmente per i rispettivi versori.
e infatti, così facendo, e pi cambiando dei segni e sommando membro a membro , risulta :
$(m_a +m_b +m_c) *a = (m_b - m_c) * g $
da cu s ricava $a$ .
Questa eq. si poteva scrivere subito :
Forza motrice $m_b*g$ meno forza resistente $m_c*g$ uguale massa totale x accelerazione $a$ . Le tensioni sono forze interne al sistema.
Grazie mille, davvero sei stato gentilissimo. Capito tutto, Stupenda spiegazione
Comunque capivi che il corpo $m_a$ si spostava a sinistra perchè il corpo $m_b$ è il più pesante e quindi trainava gli altri due verso sinistra, giusto?
grazie ancora
Comunque capivi che il corpo $m_a$ si spostava a sinistra perchè il corpo $m_b$ è il più pesante e quindi trainava gli altri due verso sinistra, giusto?
grazie ancora
Si, certo. Ma nei casi dubbi, che a volte non ti consentono di immaginare che cosa succederà, tieni sempre presente che la 2º eq. della Dinamica, in forma vettoriale : $\vecR = m\veca$ (dove $\vecR$ è la risultante di forze esterne) è una equazione che non fa riferimento ad alcun sistema di coordinate (salvo che il riferimento deve essere inerziale, ma questa è un'altra cosa).
I vettori li hanno inventati proprio per questo : liberarsi, quando possibile, dalle coordinate.
Ma poi è chiaro che, quando vai a proiettare questa equazione su degli assi cartesiani che hanno certi versori, devi tener conto dei versi di forze e accelerazioni. Infatti se guardi ho scritto apposta la prima equazione (e le seguenti) in questo modo :
$m_b*\veca_b = - m_b*a* \vecj =……..$
Il primo membro a sinistra è indipendente da $\vecj$ , ma il secondo no! E nel secondo infatti ho messo il segno $-$, prevedendo il verso della accelerazione di $m_b$.
I vettori li hanno inventati proprio per questo : liberarsi, quando possibile, dalle coordinate.
Ma poi è chiaro che, quando vai a proiettare questa equazione su degli assi cartesiani che hanno certi versori, devi tener conto dei versi di forze e accelerazioni. Infatti se guardi ho scritto apposta la prima equazione (e le seguenti) in questo modo :
$m_b*\veca_b = - m_b*a* \vecj =……..$
Il primo membro a sinistra è indipendente da $\vecj$ , ma il secondo no! E nel secondo infatti ho messo il segno $-$, prevedendo il verso della accelerazione di $m_b$.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo