Forze apparenti
Scusate vorrei dei chiarimenti rispetto ad un affermazione del proff.
Lui dice che assumendo che la Terra perfettamente sferica la forza di gravita' e' diversa sulla Terra più precisamente e' massima ai poli e minima all'equatore.
Raginandoci un po' considerando che la Terra e' un sistema di riferimenti non inerziale, possiamo dire che la forza centrifuga e' la forza che si oppone alla forza di gravita', sull'equatore la rotazione e' massima mentre ai poli e' nulla e qundi ritorno al arginamento del proff.
Ora quello che mi domando la forza centrifuga e' la forza di coriolis o sono due forze apparenti distinte?
Grazie a presto
Lui dice che assumendo che la Terra perfettamente sferica la forza di gravita' e' diversa sulla Terra più precisamente e' massima ai poli e minima all'equatore.
Raginandoci un po' considerando che la Terra e' un sistema di riferimenti non inerziale, possiamo dire che la forza centrifuga e' la forza che si oppone alla forza di gravita', sull'equatore la rotazione e' massima mentre ai poli e' nulla e qundi ritorno al arginamento del proff.
Ora quello che mi domando la forza centrifuga e' la forza di coriolis o sono due forze apparenti distinte?
Grazie a presto
Risposte
Sono diverse. Da Wikipedia:
Nell'effettuare misure con una bilancia su un corpo fermo ( $ \vec{v}_B = 0 $ ), supponendo $ \frac{d \vec{ \Omega } }{dt}=0 $ per la Terra , ottieni l'effetto da te descritto per colpa della sola forza centrifuga.
Here, the first term is the Coriolis force, the second term is the centrifugal force, and the third term is the Euler force.
Nell'effettuare misure con una bilancia su un corpo fermo ( $ \vec{v}_B = 0 $ ), supponendo $ \frac{d \vec{ \Omega } }{dt}=0 $ per la Terra , ottieni l'effetto da te descritto per colpa della sola forza centrifuga.


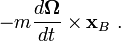

 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo