Esercizio sul bilanciamento delle forze in meccanica
Oggi vi presento un punto di un esercizio che sembra semplice, ma mi risulta altamente ostico :
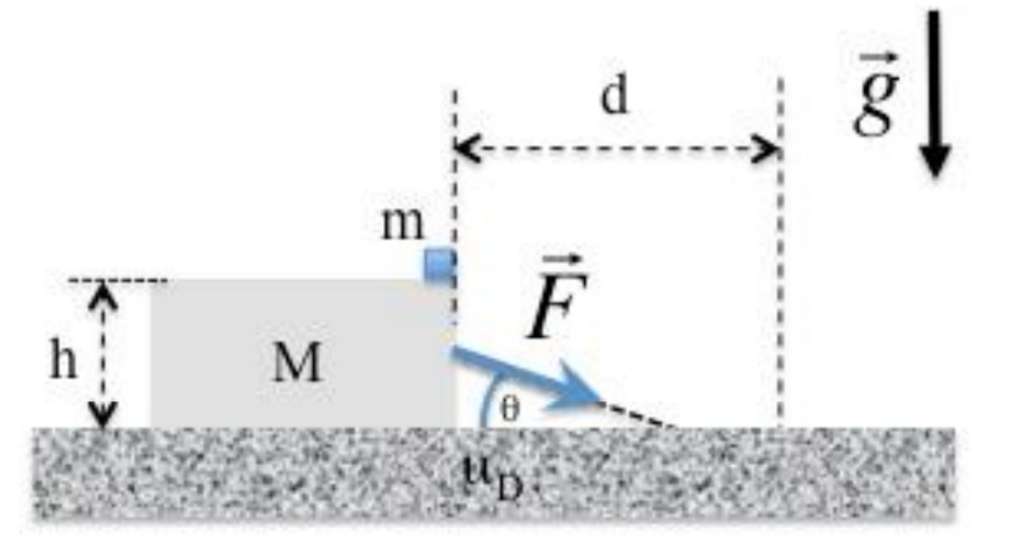
Si consideri un blocco di massa M=1.35 kg posto su un piano orizzontale scabro con
coefficiente di attrito dinamico µD=0.250 a cui è applicata una forza costante F che forma
con l'orizzontale un angolo $\theta $ =40 gradi
, cosicché la forza F (di modulo 10.7 N) ha una
componente diretta verso il basso. Al di sopra del blocco M viene posto un oggetto di
massa m=419 g di dimensioni trascurabili, che può essere considerato puntiforme. Tra il
punto materiale m ed il blocco M vi è attrito. In tali condizioni l'attrito fa sì che non vi sia
moto relativo tra i due corpi. Se i due corpi sono inizialmente fermi, calcolare:
l'accelerazione con cui i due corpi si muovono
Allora io per risolverlo ho provato in più modi diversi e quello che si avvicina di più al risultato di 1.21 ms^-2 è :
$$ \sum F_{y} = 0 quindi: - Fsin(\theta) - (M+m) g - (m+M) asin(\theta) + R = 0$$ (dove R è la reazione vincolare), mentre $$ \sum F_{x} = (M+m) acos(\theta) quindi : Fcos(\theta) - \mu _{d} R = (M+m) a cos (\theta)$$
Dove ho sbagliato? In caso avessi sbagliato, come andrebbe fatto? Grazie in anticipo
Si consideri un blocco di massa M=1.35 kg posto su un piano orizzontale scabro con
coefficiente di attrito dinamico µD=0.250 a cui è applicata una forza costante F che forma
con l'orizzontale un angolo $\theta $ =40 gradi
, cosicché la forza F (di modulo 10.7 N) ha una
componente diretta verso il basso. Al di sopra del blocco M viene posto un oggetto di
massa m=419 g di dimensioni trascurabili, che può essere considerato puntiforme. Tra il
punto materiale m ed il blocco M vi è attrito. In tali condizioni l'attrito fa sì che non vi sia
moto relativo tra i due corpi. Se i due corpi sono inizialmente fermi, calcolare:
l'accelerazione con cui i due corpi si muovono
Allora io per risolverlo ho provato in più modi diversi e quello che si avvicina di più al risultato di 1.21 ms^-2 è :
$$ \sum F_{y} = 0 quindi: - Fsin(\theta) - (M+m) g - (m+M) asin(\theta) + R = 0$$ (dove R è la reazione vincolare), mentre $$ \sum F_{x} = (M+m) acos(\theta) quindi : Fcos(\theta) - \mu _{d} R = (M+m) a cos (\theta)$$
Dove ho sbagliato? In caso avessi sbagliato, come andrebbe fatto? Grazie in anticipo
Risposte
Wait sorry ho trovato il mio errore, andava bene cone avevo scritto prima, cioè la somma forza in y uguale 0 (senza la castroneria del $(m+M) a sin(\theta) $ e la somma forze in x uguale a (M+m)a
Il problema sono in realtà tre problemi in uno.
1) la forza non basta a spostarli $F<=mu_1(m_1+m_2)g=F_((1-2) at) $
2) i corpi si muovono con accelerazioni diverse
3)i corpi si muovono con la stessa accelerazione $a_1=a_2=(F-F_((1-2) at)) /(m_1+m_2)$
Quando $ (mu_1+mu_2)/(m_1+m_2)g>F>F_((1-2)at) $
Veniamo al punto 2:
$m_1: F-mu_1(m_1+m_2)g-mu_2m_2g=m_1a_1$
$m_2:mu_2m_2g=m_2a_2$
Risulta quindi $a_1>a_2 $ se si ha $ F>(mu_1+mu_2)(m_1+m_2)g$$>F_((1-2)at) $
Se risolvi il sistema trovi $a_2=mu_2g$ costante e $a_1$ variabile
1) la forza non basta a spostarli $F<=mu_1(m_1+m_2)g=F_((1-2) at) $
2) i corpi si muovono con accelerazioni diverse
3)i corpi si muovono con la stessa accelerazione $a_1=a_2=(F-F_((1-2) at)) /(m_1+m_2)$
Quando $ (mu_1+mu_2)/(m_1+m_2)g>F>F_((1-2)at) $
Veniamo al punto 2:
$m_1: F-mu_1(m_1+m_2)g-mu_2m_2g=m_1a_1$
$m_2:mu_2m_2g=m_2a_2$
Risulta quindi $a_1>a_2 $ se si ha $ F>(mu_1+mu_2)(m_1+m_2)g$$>F_((1-2)at) $
Se risolvi il sistema trovi $a_2=mu_2g$ costante e $a_1$ variabile
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo