Esercizio su momento d'inerzia ed energia
avrei bisogno del vostro aiuto per questo esercizio:
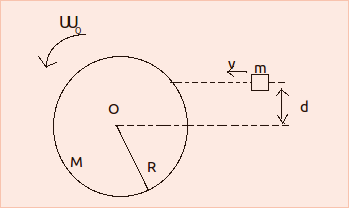
Un disco omogeneo di raggio $R=50 cm$ e massa $M=2Kg$ ruota attorno ad un asse passante per il suo centro $O$ e ortogonale al piano della figura con velocità angolare costante $\omega_0 =1,5 (rad)/s$. Un proiettile di massa $m=5g$ muovendosi orizzontalmente su una retta distante $d=30cm$ da $O$ raggiunge il disco con velocità $v=200m/s$ e resta conficcato sul bordo. Calcolare il momento di inerzia e la velocità angolare del sistema dopo l'urto, la percentuale di energia meccanica complessiva dissipata nell'urto.
io l'ho risolto così:
il disco prima dell'urto ha velocità $V = \omega_0 R$
l'urto è completamente anelastico quindi $MV+mv = (M+m)v_{CM} rArr v_{CM} =(MV+mv)/(M+m)$
Il centro di massa dopo l'urto si sposta di una quantità $y = m/(M+m)d$
Il momento di inerzia del sistema va calcolato come quello di disco che ruota su un asse spostato di y rispetto al centro di massa, no? quindi $I = 1/2 (M+m)(R-y)^2 +(M+m)y^2$
La velocità angolare dopo l'urto si ricava da $L=dmv+RMV= I \omega rArr \omega = L/I$
Per quando riguarda l'energia non ho ben chiaro cosa vuol dire "l'energia meccanica complessiva", io l'ho interpretato semplicemente come
energia prima dell'urto: $E_0 = 1/2I_0 ( \omega_0 )^2$ dove $I_0 = 1/2MR^2$
energia dopo l'urto: $E = 1/2I( \omega)^2$
da cui la percentuale di energia dissipata $E/E_0$
è giusto così?
Un disco omogeneo di raggio $R=50 cm$ e massa $M=2Kg$ ruota attorno ad un asse passante per il suo centro $O$ e ortogonale al piano della figura con velocità angolare costante $\omega_0 =1,5 (rad)/s$. Un proiettile di massa $m=5g$ muovendosi orizzontalmente su una retta distante $d=30cm$ da $O$ raggiunge il disco con velocità $v=200m/s$ e resta conficcato sul bordo. Calcolare il momento di inerzia e la velocità angolare del sistema dopo l'urto, la percentuale di energia meccanica complessiva dissipata nell'urto.

io l'ho risolto così:
il disco prima dell'urto ha velocità $V = \omega_0 R$
l'urto è completamente anelastico quindi $MV+mv = (M+m)v_{CM} rArr v_{CM} =(MV+mv)/(M+m)$
Il centro di massa dopo l'urto si sposta di una quantità $y = m/(M+m)d$
Il momento di inerzia del sistema va calcolato come quello di disco che ruota su un asse spostato di y rispetto al centro di massa, no? quindi $I = 1/2 (M+m)(R-y)^2 +(M+m)y^2$
La velocità angolare dopo l'urto si ricava da $L=dmv+RMV= I \omega rArr \omega = L/I$
Per quando riguarda l'energia non ho ben chiaro cosa vuol dire "l'energia meccanica complessiva", io l'ho interpretato semplicemente come
energia prima dell'urto: $E_0 = 1/2I_0 ( \omega_0 )^2$ dove $I_0 = 1/2MR^2$
energia dopo l'urto: $E = 1/2I( \omega)^2$
da cui la percentuale di energia dissipata $E/E_0$
è giusto così?
Risposte
taly,
ma sei sicuro/a che l'asse di rotazione non sia fisso, e cioè che si sposti dopo l'urto? Nella traccia non c'è cenno ad una velocità iniziale di traslazione del disco, che potrebbe anche essere zero , ma comunque il testo dovrebbe dirlo.
Secondo me, l'asse è fisso, il disco ruota soltanto.
Certamente l'urto è anelastico, quindi l'energia cinetica non si conserva.
Se poi l'asse è fisso, e il disco ruota senza attrito (come suppongo), neppure la quantità di moto si conserva, l'asse esercita un impulso durante l'urto. Però, ruotando senza attrito, non può esercitare momento resistente. Perciò qui secondo me si conserva solo il momento angolare totale di (disco più proiettile) : bisogna uguagliare le espressioni del momento angolare totale del sistema, prima e dopo l'urto anelastico, tenendo conto che anche il proiettile ha un momento angolare rispetto all'asse del disco.
Se è come penso, dovrebbe aversi ( non vorrei sbagliarmi) :
$ L_0 = I_0*\omega_0 + mvd $ , dove $L_0$ è il momento angolare prima dell'urto, e $I_0$ il momento di inerzia del disco, sempre prima dell'urto. L'altro termine è il momento angolare del proiettile, prima dell'urto, rispetto all'asse di rotazione.
$L_f = I_f*\omega_f = (m*d^2 + I_0)*\omega_f$ , dove $I_(f) = m*d^2 + I_0 $ è il momento di inerzia finale rispetto allo stesso asse, e $\omega_f$ la velocità angolare finale.
Perciò uguagliando si ricava che : $ \omega_f = (I_0*\omega_0 + mvd )/(m*d^2 + I_0)$
ma sei sicuro/a che l'asse di rotazione non sia fisso, e cioè che si sposti dopo l'urto? Nella traccia non c'è cenno ad una velocità iniziale di traslazione del disco, che potrebbe anche essere zero , ma comunque il testo dovrebbe dirlo.
Secondo me, l'asse è fisso, il disco ruota soltanto.
Certamente l'urto è anelastico, quindi l'energia cinetica non si conserva.
Se poi l'asse è fisso, e il disco ruota senza attrito (come suppongo), neppure la quantità di moto si conserva, l'asse esercita un impulso durante l'urto. Però, ruotando senza attrito, non può esercitare momento resistente. Perciò qui secondo me si conserva solo il momento angolare totale di (disco più proiettile) : bisogna uguagliare le espressioni del momento angolare totale del sistema, prima e dopo l'urto anelastico, tenendo conto che anche il proiettile ha un momento angolare rispetto all'asse del disco.
Se è come penso, dovrebbe aversi ( non vorrei sbagliarmi) :
$ L_0 = I_0*\omega_0 + mvd $ , dove $L_0$ è il momento angolare prima dell'urto, e $I_0$ il momento di inerzia del disco, sempre prima dell'urto. L'altro termine è il momento angolare del proiettile, prima dell'urto, rispetto all'asse di rotazione.
$L_f = I_f*\omega_f = (m*d^2 + I_0)*\omega_f$ , dove $I_(f) = m*d^2 + I_0 $ è il momento di inerzia finale rispetto allo stesso asse, e $\omega_f$ la velocità angolare finale.
Perciò uguagliando si ricava che : $ \omega_f = (I_0*\omega_0 + mvd )/(m*d^2 + I_0)$
anche secondo me l'asse rimane fisso, avevo calcolato il momento di inerzia in quel modo perchè consideravo l'insieme disco+proiettile un unico corpo ruotante attorno ad un asse non passante per il centro di massa. grazie ai tuoi suggerimenti ho capito di averlo sbagliato, però mi rimangono dei dubbi: tu scrivi $I_f=m⋅d^2+I_0 $ e immagino sia il terorema di Huygens-Steiner, ma non capisco bene perchè in questa forma... non devo considerare la massa totale del sistema disco+proiettile invece di $m$, massa del solo proiettile, e la distanza del centro di massa dall'asse, quindi $y$ invece della distanza $d$ del proiettile dall'asse?
per quanto riguarda il calcolo della percentuale di energia invece, è corretto?
per quanto riguarda il calcolo della percentuale di energia invece, è corretto?
"taly":
anche secondo me l'asse rimane fisso, avevo calcolato il momento di inerzia in quel modo perchè consideravo l'insieme disco+proiettile un unico corpo ruotante attorno ad un asse non passante per il centro di massa. grazie ai tuoi suggerimenti ho capito di averlo sbagliato, però mi rimangono dei dubbi: tu scrivi $I_f=m⋅d^2+I_0 $ e immagino sia il terorema di Huygens-Steiner, ma non capisco bene perchè in questa forma... non devo considerare la massa totale del sistema disco+proiettile invece di $m$, massa del solo proiettile, e la distanza del centro di massa dall'asse, quindi $y$ invece della distanza $d$ del proiettile dall'asse?
per quanto riguarda il calcolo della percentuale di energia invece, è corretto?
E infatti, ora che mi ci fai pensare, mi accorgo che forse ho sbagliato io a copiare i miei appunti, che non ho più : il momento di inerzia finale, rispetto allo stesso asse di rotazione supposto fisso, dovrebbe essere : $ I_f = I_o + m*R^2$ , dove $R$ è il raggio del disco, poichè il proiettile rimane conficcato nel bordo. Il momento di inerzia è additivo, se aggiungi una massa $m$ a una distanza$R$ dall'asse il mom. di inerzia aumenta di $m*R^2$. Huygens non c'entra,scusami!
Comunque, poco male. Correggi l'espressione di $I_f$ , e quindi dovresti avere ( uguagliando i momenti angolari) che la velocità angolare finale vale :
$\omega_f = (I_0\omega_0 + mvd)/(mR^2 + I_0)$
Per quanto riguarda l'energia cinetica, quella iniziale è data dalla somma di due termini : l'en cinetica rotazionale iniziale del solo disco $1/2*I_0*\omega_0^2$ PIU' l'en cinetica di traslazione del proiettile $1/2*m*v^2$ : conosci tutte le quantità coinvolte.
Invece l'en cinetica finale è data da $ 1/2*I_f*\omega_f^2$ , dove pure conosci le quantità.
Se calcoli la differenza tra l'en cinetica iniziale e quella finale, analiticamente ( attenzione, perchè i passaggi sono un pò brigosi!) vedrai che la differenza è una certa espressione, che è sempre positiva qualunque sia il valore della velocità del proiettile $v$ . Perciò l'energia cinetica finale è sempre minore di quella iniziale.
Comunque , lo puoi verificare anche direttamente introducendo le quantità numeriche fin dall'inizio.
Ok, grazie navigatore, adesso è tutto chiaro, la risoluzione corretta allora è questa:
$L_0 = I_0 \omega_0 + mvd = 1/2MR^2 \omega_0 + mvd$
$ L_f $ $ = I_f$$omega_f $ $= 1/2 (M+m) R^2 \omega_f $
$L_0 = L_f$ quindi $\omega_f = (1/2MR^2 \omega_0 + mvd)/(1/2(M+m)R^2)$
$E_0 = 1/2I_0 \omega_0 ^2 + 1/2mv^2 = 1/4MR^2 \omega_0 ^2 + 1/2mv^2$
$ E_f = 1/2 I_f$$omega_f ^2 $ $ = 1/4 (M+m) R^2 (1/2M R^2 \omega_0 + mvd)/(1/2 (M+m) R^2) $ $= 1/2 (1/2M R^2 \omega_0 + mvd) = 1/2 L_0 $
percentuale di energia = $E_0 - E_f = 1/4 [MR^2 \omega_0 (\omega_0 - 1) + 2mv(v-d)]$
esatto?
$L_0 = I_0 \omega_0 + mvd = 1/2MR^2 \omega_0 + mvd$
$ L_f $ $ = I_f$$omega_f $ $= 1/2 (M+m) R^2 \omega_f $
$L_0 = L_f$ quindi $\omega_f = (1/2MR^2 \omega_0 + mvd)/(1/2(M+m)R^2)$
$E_0 = 1/2I_0 \omega_0 ^2 + 1/2mv^2 = 1/4MR^2 \omega_0 ^2 + 1/2mv^2$
$ E_f = 1/2 I_f$$omega_f ^2 $ $ = 1/4 (M+m) R^2 (1/2M R^2 \omega_0 + mvd)/(1/2 (M+m) R^2) $ $= 1/2 (1/2M R^2 \omega_0 + mvd) = 1/2 L_0 $
percentuale di energia = $E_0 - E_f = 1/4 [MR^2 \omega_0 (\omega_0 - 1) + 2mv(v-d)]$
esatto?
"taly":
Ok, grazie navigatore, adesso è tutto chiaro, la risoluzione corretta allora è questa:
$L_0 = I_0 \omega_0 + mvd = 1/2MR^2 \omega_0 + mvd$
$ L_f $ $ = I_f$$omega_f $ $= 1/2 (M+m) R^2 \omega_f $
Mi pare che dovrebbe essere : $ I_f = (1/2*M+m)*R^2$ , cioè il fattore $1/2$ riguarda solo il disco. LA massa aggiunta $m$ è a distanza $R$ , giusto ? Quindi dovresti rivedere il tutto.
La procedura comunque mi sembra corretta.Che esercizio incasinato!
"navigatore":
Mi pare che dovrebbe essere : $ I_f = (1/2*M+m)*R^2$
si è così, è stato uno stupido errore di distrazione che purtroppo mi sono trascinata per tutto l'esercizio
grazie mille navigatore per avermi aiutata ad uscire da questo esercizio davvero incasinato
Ok, la cosa importante è capire lo svolgimento, quindi la Fisica prima delle formule.
Mi raccomando , eh! Ora che hai capito la procedura, fai per bene i passaggi!
Ciao, alla prossima.
Mi raccomando , eh! Ora che hai capito la procedura, fai per bene i passaggi!
Ciao, alla prossima.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo