Errore concettuale
Ho fatto un ragionamento ma è scorretto e non trovo dove sto sbagliando. Questo è il ragionamento:
\[ E_c = \frac{1}{2}mv^2\]
\[F=ma\]
se applico una forza \(F\) a una massa \(m\) questa accelera e la velocità risulta:
\[\dot{v}=\frac{F}{m} \]
\[v(t)=v_0+t\frac{F}{m} \]
la variazione dell'energia cinetica tra \(t_0\) e \(t\) è quindi:
\[\Delta E_c(t)=\frac{1}{2}m(t\frac{F}{m})^2\]
\[\Delta E_c(t)=\frac{1}{2}\frac{F^2}{m}t^2\]
quindi l'energia cinetica aumenta quadraticamente con il tempo. Ma in un sistema chiuso in cui esiste una macchina ideale che usi un carburante per fornire la forza \(F\), ha necessità di diminuire la propria energia interna di \(\Delta E(t)\) pari a:
\[\Delta E(t)+\Delta E_c(t)=0\]
quindi il consumo di carburante della macchina ideale a rendimento unitario sarà pari a:
\[\Delta E(t)=-kt^2\]
ovvero il carburante sarà consumato non in modo costante con il tempo ma in modo quadratico. Questo non è coerente con un'auto ideale che accelera in cui il consumo di carburante è costante nel tempo. Dovrebbe essere \(\Delta E(t)=-kt\)
Non mi rendo conto dove sto sbagliando.
\[ E_c = \frac{1}{2}mv^2\]
\[F=ma\]
se applico una forza \(F\) a una massa \(m\) questa accelera e la velocità risulta:
\[\dot{v}=\frac{F}{m} \]
\[v(t)=v_0+t\frac{F}{m} \]
la variazione dell'energia cinetica tra \(t_0\) e \(t\) è quindi:
\[\Delta E_c(t)=\frac{1}{2}m(t\frac{F}{m})^2\]
\[\Delta E_c(t)=\frac{1}{2}\frac{F^2}{m}t^2\]
quindi l'energia cinetica aumenta quadraticamente con il tempo. Ma in un sistema chiuso in cui esiste una macchina ideale che usi un carburante per fornire la forza \(F\), ha necessità di diminuire la propria energia interna di \(\Delta E(t)\) pari a:
\[\Delta E(t)+\Delta E_c(t)=0\]
quindi il consumo di carburante della macchina ideale a rendimento unitario sarà pari a:
\[\Delta E(t)=-kt^2\]
ovvero il carburante sarà consumato non in modo costante con il tempo ma in modo quadratico. Questo non è coerente con un'auto ideale che accelera in cui il consumo di carburante è costante nel tempo. Dovrebbe essere \(\Delta E(t)=-kt\)
Non mi rendo conto dove sto sbagliando.
Risposte
Qui:
Perché in realtà:
\[
\Delta E_c(t)=\frac{1}{2}m v(t)^2 - \frac{1}{2}m v_0^2 = \frac{1}{2}\frac{F^2 t^2}{m}+ v_0 t F
\]
è certamente un errore, ma non credo che giustifichi il tuo argomento - che premetto di non averlo letto con attenzione.
esempio:
perché dici questo? considera un'auto in autostrada. Mica accelera sempre, altrimenti a quest'ora saresti senza patente. Accelera in momenti limitati (entrate, ripartenze da caselli, etc etc), per il resto del tempo si muove a velocità più o meno costante, e usa energia quanto basta per compensare le perdite dovute alla resistenza all'avanzamento (attriti gomma/strada, drag etc etc). Detto in altri termini, se consideri il caso ideali che suggerisci trascurando tutte le perdite di energie in attriti (non solo quelli menzionati, ma anche meccanici + inefficenze date dalla combustione, tieni conto che il circa il 70% dell'energia va farsi a benedire!), per conservazione dell'energia deve aumentare sì quadraticamente.
Per chiarire ulteriormente, non serve pensare all'auto che si muove. Prendi un oggetto su un piano liscio e muovilo: l'energia che fornisci per aumentare la sua velocità di 1 km/h in 1 secondo è ben diversa se la velocità iniziale del corpo è zero, oppure se è già in movimento a 10 km/h. Tradotto nell'esempio della macchina, se essa si muove con accelerazione costante, l'energia che consuma per incrementare di 10km/h la sua velocità in 1 secondo è ben maggiore se essa si trova ad una velocità iniziale di 100km/h rispetto alla partenza da fermo, quindi il consumo di carburante non può essere costante.
ma probabilmente mi sto perdendo cosa intendevi dire ..
\[ \Delta E_c(t)=\frac{1}{2}m(t\frac{F}{m})^2 \]
Perché in realtà:
\[
\Delta E_c(t)=\frac{1}{2}m v(t)^2 - \frac{1}{2}m v_0^2 = \frac{1}{2}\frac{F^2 t^2}{m}+ v_0 t F
\]
è certamente un errore, ma non credo che giustifichi il tuo argomento - che premetto di non averlo letto con attenzione.
esempio:
è coerente con un'auto ideale che accelera in cui il consumo di carburante è costante nel tempo
perché dici questo? considera un'auto in autostrada. Mica accelera sempre, altrimenti a quest'ora saresti senza patente. Accelera in momenti limitati (entrate, ripartenze da caselli, etc etc), per il resto del tempo si muove a velocità più o meno costante, e usa energia quanto basta per compensare le perdite dovute alla resistenza all'avanzamento (attriti gomma/strada, drag etc etc). Detto in altri termini, se consideri il caso ideali che suggerisci trascurando tutte le perdite di energie in attriti (non solo quelli menzionati, ma anche meccanici + inefficenze date dalla combustione, tieni conto che il circa il 70% dell'energia va farsi a benedire!), per conservazione dell'energia deve aumentare sì quadraticamente.
Per chiarire ulteriormente, non serve pensare all'auto che si muove. Prendi un oggetto su un piano liscio e muovilo: l'energia che fornisci per aumentare la sua velocità di 1 km/h in 1 secondo è ben diversa se la velocità iniziale del corpo è zero, oppure se è già in movimento a 10 km/h. Tradotto nell'esempio della macchina, se essa si muove con accelerazione costante, l'energia che consuma per incrementare di 10km/h la sua velocità in 1 secondo è ben maggiore se essa si trova ad una velocità iniziale di 100km/h rispetto alla partenza da fermo, quindi il consumo di carburante non può essere costante.
ma probabilmente mi sto perdendo cosa intendevi dire ..
"Lampo1089":
Qui:
\[ \Delta E_c(t)=\frac{1}{2}m(t\frac{F}{m})^2 \]
Perché in realtà:
\[ \Delta E_c(t)=\frac{1}{2}m v(t)^2 - \frac{1}{2}m v_0^2 = \frac{1}{2}\frac{F^2 t^2}{m}+ v_0 t F \]
è certamente un errore, ma non credo che giustifichi il tuo argomento - che premetto di non averlo letto con attenzione.
Giusto, volevo semplificare il calcolo ma ho sbagliato. Comunque possiamo considerare \(v_0=0\) per rientrare nel ragionamento.
esempio:
[quote]è coerente con un'auto ideale che accelera in cui il consumo di carburante è costante nel tempo
perché dici questo? considera un'auto in autostrada. Mica accelera sempre, altrimenti a quest'ora saresti senza patente. Accelera in momenti limitati (entrate, ripartenze da caselli, etc etc), per il resto del tempo si muove a velocità più o meno costante, e usa energia quanto basta per compensare le perdite dovute alla resistenza all'avanzamento (attriti gomma/strada, drag etc etc). Detto in altri termini, se consideri il caso ideali che suggerisci trascurando tutte le perdite di energie in attriti (non solo quelli menzionati, ma anche meccanici + inefficenze date dalla combustione, tieni conto che il circa il 70% dell'energia va farsi a benedire!), per conservazione dell'energia deve aumentare sì quadraticamente.[/quote]
Ecco, mi pare che tu abbia colto il punto. Un razzo che sta partendo per lo spazio ha una forza di propulsione superiore a \(mg\) e con un consumo costante di carburante accelera fino alla velocità di fuga.
Per chiarire ulteriormente, non serve pensare all'auto che si muove. Prendi un oggetto su un piano liscio e muovilo: l'energia che fornisci per aumentare la sua velocità di 1 km/h in 1 secondo è ben diversa se la velocità iniziale del corpo è zero, oppure se è già in movimento a 10 km/h. Tradotto nell'esempio della macchina, se essa si muove con accelerazione costante, l'energia che consuma per incrementare di 10km/h la sua velocità in 1 secondo è ben maggiore se essa si trova ad una velocità iniziale di 100km/h rispetto alla partenza da fermo, quindi il consumo di carburante non può essere costante.
Ma se cambi sistema di riferimento l'auto che va a 100km/h risulta ferma mentre la benzina che hai consumato per portarla da 100 a 110 km/h risulta concreta e non può essere differente a seconda del sistema di riferimento inerziale. Giusto?
ma probabilmente mi sto perdendo cosa intendevi dire ..
mi pare tu abbia colto il punto.
Ecco, mi pare che tu abbia colto il punto. Un razzo che sta partendo per lo spazio ha una forza di propulsione superiore a mg e con un consumo costante di carburante accelera fino alla velocità di fuga.
Assumiamo per assurdo che un oggetto che accelera costantemente per azione di una forza F costante consumi nel tempo una quantità costante carburante - che tradotto significa che converta energia (qualunque sia fonte) in energia cinetica con un rate costante. (consideriamo una situazione 1D, così possiamo evitare di appesantire la notazione con i vettori). Inoltre supponiamo che l'oggetto sia inizialmente fermo. Trascuriamo ovviamente tutti gli attriti, ossia che l'energia totale del sistema (cinetica + potenziale - qualsiasi sia la sua natura) sia conservata.
ovviamente, questo significa in termini di derivate:
\[
\frac{dK}{dt} + \frac{dU}{dt} = 0
\]
e a causa delle assunzioni \(\frac{dU}{dt} = -c \) con c una costante positiva. Inoltre è ben noto che:
\[
\frac{dK}{dt} = F v(t) = \frac{F^2 t}{m}
\]
e quindi dovrebbe essere soddisfatta l'uguaglianza ad ogni tempo:
\[
\frac{F^2 t}{m} = c
\]
Ovviamente non è possibile, si giunge ad un assurdo. Ergo, l'ipotesi iniziale - che il consumo di carburante possa essere costante in tale moto - è falsa.
Un simile moto violerebbe la conservazione dell'energia.
Ho ragionato in termini di potenza di una forza, ma se noti è esattamente lo stesso ragionamento che fai tu in termini di differenze di energie ad istanti diversi. In ogni caso non si scappa: se consideri un sistema conservativo, per definizione l'energia totale deve conservarsi. E se non si conserva, deve esserci un'errore nelle tue assunzioni. L'unica altra tua assunzione è il consumo di carburante, o meglio la velocità con cui varia l'energia potenziale, che ipotizzi costante: alla luce dell'assurdo a cui giungi, l'errore è proprio quello.
Sei ancora convinto che un oggetto che accelera possa consumare energia con rateo costante?
"Lampo1089":
\[
\frac{dK}{dt} + \frac{dU}{dt} = 0
\]
U sarebbe l'energia chimica del propellente del razzo o dell'automobile.
e a causa delle assunzioni \(\frac{dU}{dt} = -c \) con c una costante positiva. Inoltre è ben noto che:
\[
\frac{dK}{dt} = F v(t) = \frac{F^2 t}{m}
\]
che sono anche le formule che ho usato io.
e quindi dovrebbe essere soddisfatta l'uguaglianza ad ogni tempo:
\[
\frac{F^2 t}{m} = c
\]
Ovviamente non è possibile, si giunge ad un assurdo.
ok hai fatto una dimostrazione per assurdo.
Sei ancora convinto che un oggetto che accelera possa consumare energia con rateo costante?
Saresti così gentile da spiegarmi anche come mai (l'energia cinetica dipende dal sistema di riferimento, questo lo so) il consumo di carburante della nostra auto e del nostro missile dipende dal sistema di riferimento scelto?
intendo dire che il consumo di carburante nell'unità di tempo è circa pari a:
\[
\frac{dK}{dt} \cdot 1s = F v(t) \cdot 1s
\]
se scelgo un sistema di riferimento solidale alla velocità 0 m/s ottengo che a 10 m/s il consumo è di \( F \cdot 10 m \) in 1 s, mentre se scelgo un sistema di riferimento solidale alla velocità di 10 m/s il consumo di carburante in 1 secondo è circa uguale a 0.
In altre parole prendiamo un'auto ideale che corre su una strada dritta insieme a una seconda auto su cui è installato il sistema di riferimento e che corre a 10 m/s, rispetto alla seconda auto la prima auto è ferma quando accelerando da 0 a alla velocità massima sotto l'azione di una forza, raggiunge la velocità di 10 m/s. In quel momento \( F v(t) \cdot 1s \) è il consumo di carburarante nel tempo di 1 s mediante una approssimazione lineare, essendo \( v(t) = 0 \) si ha che il consumo è circa zero.
Invece rispetto al pedone che se ne sta fermo la prima auto ha velocità \( v(t) = 10 m/s \) e il consumo di carburante è ingente.
"mgrau":
Anni fa c'è stata una questione analoga alla tua, molto combattuta
Grazie del link mgrau, mi era sfuggita la discussione. Ho letto tutto il thread e l'ho trovata interessante, mi è piaciuto l'esempio della molla con le due masse uguali all'estremità che mi pare tu abbia fatto insieme a @Pazzuzu, puoi la discussione è degenerata come spesso accade.
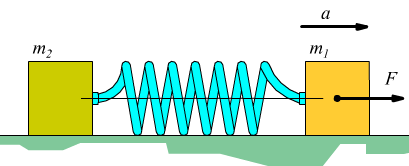
Comunque se \( m_1 = m_2 \quad \textrm{e} \quad F_{1x} = F, \quad F_{2x} = -F, \quad v_{1x} = \frac{1}{2} v, \quad v_{2x} = - \frac{1}{2} v \)
allora dalla:
\[ \frac{dK}{dt} + \frac{dU}{dt} = 0 \]
con \( \dot K = F_{1x} v_{1x} + F_{2x} v_{2x} = Fv \)
risulta che la diminuzione dell'energia interna della molla nell'unità di tempo, \( \frac{dU}{dt} \), che in altri termini è il consumo di combustibile nell'unità di tempo di una auto ideale che va a velocità \( v \) rispetto al terreno e che accelera, dipende dalla velocità della massa \( m_1 \).
Dall'altro lato il centro di massa delle due masse \( m_1 \, m_2 \) non si muove oppure si muove a velocità costante dipendente dal sistema di riferimento scelto, inoltre la massa \( m_2 \) si muove accelerando sotto la forza \( -F \) che nel caso dell'auto ideale corrisponde al fatto che la terra si sposta in direzione contraria a quella dell'auto (con un lavoro trascurabile). Non muovendosi il centro di massa l'energia cinetica del sistema è nulla o costante (dipende dal sistema di riferimento inerziale).
Se si cambia il sistema di riferimento allora la massa \( m_1 \) può pure risultare ferma ma la massa \( m_2 \) avrà una energia cinetica molto più elevata dando lo stesso consumo di carburante nell'unità di tempo e pari a \( Fv \).
***
Invece è molto più evidente la stessa questione nel caso della caduta dei gravi.
Man mano che la massa \( m \) cade al suolo (senza cambiare il sistema di riferimento agganciato alla terra) la forza peso \( mg \) agisce ed è costante in un largo intervallo di altezza, inoltre la particella accelera e diminuisce la sua altezza e quindi l'energia potenziale \( mgh \), più va veloce e più cala \( h \) e quindi più cala il "carburante" \( mgh \) che si può vedere come la benzina consumata da un'auto sottoposta alla forza \( F = mg \).
Quindi se il grave cadesse a velocità costante, \( h \) diminuirebbe in modo lineare e pure la "benzina" \( mgh \) ma quindi non sarebbe sottoposto a una forza che per definizione fa accelerare il grave che si "mangia" l'energia potenziale in modo sempre più veloce ovvero si mangia la benzina in modo sempre più veloce.
Se si cambia sistema di riferimento occorre come nel caso della molla considerare il sistema grave-terra dove la terrà si muoverà di pochissimo incontro al grave ma ha una massa enorme e quindi in un sistema inerziale incentrato nel punto dove è il grave che sta cadendo, la terra avrà una energia cinetica che da luogo al consumo di carburante ovvero diminuzione di energia potenziale.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo