Dubbio su conservazione dell'energia e equazione
Sono di nuovo qui per un altro problema
Il testo è :
Un dispositivo industriale elettromeccanico viene utilizzato per arrestare
piccoli oggetti in moto che si sono caricati negativamente per attrito
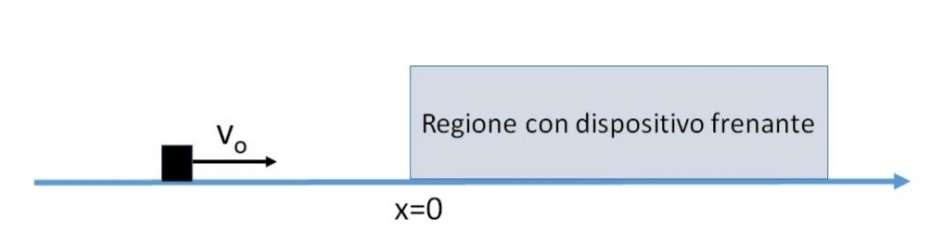
elettrostatico durante la produzione. Il moto di tali oggetti avviene (con
attrito completamente trascurabile) lungo l’asse x come da figura, con
velocità vo; il dispositivo frenante inizia ad operare a x=0, nella regione
positiva. Il modulo della forza esercitata dal dispositivo dipende dalla
posizione x (in m), ed è parametrizzabile con l’equazione:
F= q∙k∙x, dove q [misurata in Coulomb (C)] è la carica elettrica sull’oggetto
e k=0.23×106
N/(m∙C) una costante caratteristica.
1) Scrivere l’espressione del lavoro compiuto dal dispositivo per frenare
un oggetto con carica -qo dalla posizione x=0 fino a una generica
posizione xo.
2) Calcolare la distanza L percorsa da un oggetto di carica q0=-7×10-6 C,
massa m0=20.0 g, velocità iniziale v0=11.4 km/h fino al suo arresto.
3) Scrivere l’equazione differenziale che descrive il moto e la
corrispondente legge oraria, assumendo che a t=0 l’oggetto sia a x=0;
4) Calcolare il tempo t* che l’oggetto sopra descritto impiega per
fermarsi nel punto L.
5) Determinare la distanza L1 e il tempo t1* di arresto di un oggetto che
si muove con velocità v1=2v0
Ok il punto 1 è un integrale che mi da $L= - 1/2 q_{0} k x^{2}$, il problema arriva con il punto 2 perché se uso la conservazione dell'energia quindi $1/2 m v_{0}^{2} = 1/2 q_{0} k x^{2} $ dove x è L, e viene il risultato di L corretto, ho provato a trovare la L anche in un altro modo con la formula $ v^{2} = v_{0}^{2} +2aL$ dove a è $ a = - (q_{0} K L) / m_{0}$ e viene un valore sbagliato, le mie domande sono : perché viene un valore sbagliato? Come trovo il tempo che impiega per fermarsi?
Grazie in anticipo

Il testo è :
Un dispositivo industriale elettromeccanico viene utilizzato per arrestare
piccoli oggetti in moto che si sono caricati negativamente per attrito
elettrostatico durante la produzione. Il moto di tali oggetti avviene (con
attrito completamente trascurabile) lungo l’asse x come da figura, con
velocità vo; il dispositivo frenante inizia ad operare a x=0, nella regione
positiva. Il modulo della forza esercitata dal dispositivo dipende dalla
posizione x (in m), ed è parametrizzabile con l’equazione:
F= q∙k∙x, dove q [misurata in Coulomb (C)] è la carica elettrica sull’oggetto
e k=0.23×106
N/(m∙C) una costante caratteristica.
1) Scrivere l’espressione del lavoro compiuto dal dispositivo per frenare
un oggetto con carica -qo dalla posizione x=0 fino a una generica
posizione xo.
2) Calcolare la distanza L percorsa da un oggetto di carica q0=-7×10-6 C,
massa m0=20.0 g, velocità iniziale v0=11.4 km/h fino al suo arresto.
3) Scrivere l’equazione differenziale che descrive il moto e la
corrispondente legge oraria, assumendo che a t=0 l’oggetto sia a x=0;
4) Calcolare il tempo t* che l’oggetto sopra descritto impiega per
fermarsi nel punto L.
5) Determinare la distanza L1 e il tempo t1* di arresto di un oggetto che
si muove con velocità v1=2v0
Ok il punto 1 è un integrale che mi da $L= - 1/2 q_{0} k x^{2}$, il problema arriva con il punto 2 perché se uso la conservazione dell'energia quindi $1/2 m v_{0}^{2} = 1/2 q_{0} k x^{2} $ dove x è L, e viene il risultato di L corretto, ho provato a trovare la L anche in un altro modo con la formula $ v^{2} = v_{0}^{2} +2aL$ dove a è $ a = - (q_{0} K L) / m_{0}$ e viene un valore sbagliato, le mie domande sono : perché viene un valore sbagliato? Come trovo il tempo che impiega per fermarsi?
Grazie in anticipo
Risposte
"Stefano.saloma":
Ok il punto 1 è un integrale che mi da $L= - 1/2 q_{0} k x^{2}$, il problema arriva con il punto 2 perché se uso la conservazione dell'energia quindi $1/2 m v_{0}^{2} = 1/2 q_{0} k x^{2} $ dove x è L, e viene il risultato di L corretto, ho provato a trovare la L anche in un altro modo con la formula $ v^{2} = v_{0}^{2} +2aL$ dove a è $ a = - (q_{0} K L) / m_{0}$ e viene un valore sbagliato
Forse non mi sono impegnato abbastanza, ma secondo me:
1) c'è confusione fra L e $L$
2) la formula $ v^{2} = v_{0}^{2} +2aL$ dove a è $ a = - (q_{0} K L) / m_{0}$ da dove salta fuori?
Infine, la forza frenante è di tipo elastico, per cui si sa subito che il moto è armonico e si tratta quindi di trovare l'ampiezza e il periodo.
"mgrau":
[quote="Stefano.saloma"]
Ok il punto 1 è un integrale che mi da $L= - 1/2 q_{0} k x^{2}$, il problema arriva con il punto 2 perché se uso la conservazione dell'energia quindi $1/2 m v_{0}^{2} = 1/2 q_{0} k x^{2} $ dove x è L, e viene il risultato di L corretto, ho provato a trovare la L anche in un altro modo con la formula $ v^{2} = v_{0}^{2} +2aL$ dove a è $ a = - (q_{0} K L) / m_{0}$ e viene un valore sbagliato
Forse non mi sono impegnato abbastanza, ma secondo me:
1) c'è confusione fra L e $L$
[/quote]
Allora la prima L è il lavoro, la $L$ che si trova nella componente dell'acelerazione invece è lo spazio percorso, mi scuso per questa imprecisione.
"mgrau":
2) la formula $ v^{2} = v_{0}^{2} +2aL$ dove a è $ a = - (q_{0} K L) / m_{0}$ da dove salta fuori?
Infine, la forza frenante è di tipo elastico, per cui si sa subito che il moto è armonico e si tratta quindi di trovare l'ampiezza e il periodo.
Vero non avevo pensato alla risposta elastica, grazie mille per avermi cavato questo dubbio atroce
Ciao
Per il secondo punto io avrei fatto:
$1/2mv_f^2=1/2k (x_2-x_1)^2$ da cui $(x_2-x_1)=v_f sqrt(m/k) $
Dove $v_f $ e' la velocita' con cui giunge alla molla
La pulsazione della molla è $ω=sqrt(k/m) $
L'ampiezza la trovi come sopra e viene $A^2=(mv_0^2)/k$
Ti manca solo la fase iniziale che la trovi con le condizioni iniziali e l'equazione del moto armonico
E ti viene $sin(δ) =v_0/(-ωt) $
Per il secondo punto io avrei fatto:
$1/2mv_f^2=1/2k (x_2-x_1)^2$ da cui $(x_2-x_1)=v_f sqrt(m/k) $
Dove $v_f $ e' la velocita' con cui giunge alla molla
La pulsazione della molla è $ω=sqrt(k/m) $
L'ampiezza la trovi come sopra e viene $A^2=(mv_0^2)/k$
Ti manca solo la fase iniziale che la trovi con le condizioni iniziali e l'equazione del moto armonico
E ti viene $sin(δ) =v_0/(-ωt) $
"Lucacs":
Ciao
Per il secondo punto io avrei fatto:
$1/2mv_f^2=1/2k (x_2-x_1)^2$ da cui $(x_2-x_1)=v_f sqrt(m/k) $
Dove $v_f $ e' la velocita' con cui giunge alla molla
La pulsazione della molla è $ω=sqrt(k/m) $
L'ampiezza la trovi come sopra e viene $A^2=(mv_0^2)/k$
Ti manca solo la fase iniziale che la trovi con le condizioni iniziali e l'equazione del moto armonico
E ti viene $sin(δ) =v_0/(-ωt) $
Beh è un'ottima strada anche quella che suggerisce lei, grazie mille
Gli altri due punti credo che sai risolverli una volta che hai velocità e spazio percorso
"Lucacs":
Gli altri due punti credo che sai risolverli una volta che hai velocità e spazio percorso
Si gli altri due punti vengono di conseguenza


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo