Corpo e cilindro legati da una fune
Ciao a tutti, ho provato a risolvere questo problema:
Un corpo di massa m=1Kg è poggiato su un piano orizzontale scabro,con coefficiente di attrito dinamico 0.2 ed è collegato, mediante una fune che passa su una carrucola ideale, all'asse di un cilindro omogeneo di massa M=2kg. Il cilindro rotola senza strisciare su un piano con angolo di inclinazione di 30°. Calcolare: a)l'accelerazione con cui si muove il sistema; b)la tensione della fune.
Io l'ho trattato come punto materiale, c'è possibilità di trattarlo come corpo rigido con le informazioni presenti?
Diagramma Forze:
${\(T-udmg=ma),(Mgsentheta-T=Ma):}$
Essendo il filo inestensibile, i due corpi si muoveranno con la medesima accelerazione:
$-udmg+NMgsentheta=(M+m)a$
$-0.2*9.8+2*9.8*0.5=3a$
$-1.96+9.8=3a$
$a=2.62m/s^2$
Calcolo tensione T:
Mgsentheta-T=Ma
$T=19.6*0.5-5.24=4.56N$
Secondo voi è svolto correttamente? Grazie sempre
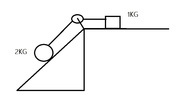
Un corpo di massa m=1Kg è poggiato su un piano orizzontale scabro,con coefficiente di attrito dinamico 0.2 ed è collegato, mediante una fune che passa su una carrucola ideale, all'asse di un cilindro omogeneo di massa M=2kg. Il cilindro rotola senza strisciare su un piano con angolo di inclinazione di 30°. Calcolare: a)l'accelerazione con cui si muove il sistema; b)la tensione della fune.
Io l'ho trattato come punto materiale, c'è possibilità di trattarlo come corpo rigido con le informazioni presenti?
Diagramma Forze:
${\(T-udmg=ma),(Mgsentheta-T=Ma):}$
Essendo il filo inestensibile, i due corpi si muoveranno con la medesima accelerazione:
$-udmg+NMgsentheta=(M+m)a$
$-0.2*9.8+2*9.8*0.5=3a$
$-1.96+9.8=3a$
$a=2.62m/s^2$
Calcolo tensione T:
Mgsentheta-T=Ma
$T=19.6*0.5-5.24=4.56N$
Secondo voi è svolto correttamente? Grazie sempre

Risposte
Perdonami, ma il momento d'inerzia del disco che fine ha fatto ?
"75america":
c'è possibilità di trattarlo come corpo rigido con le informazioni presenti?
bisognerebbe conoscere il raggio del cerchio di base


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo