Applicazione della cinematica nel piano allo sport

[iolanda.disimone]

Ciao ragazzi, il professore ci ha dato un progetto di fisica in cui dovrò comporre un elaborato discorsivo che contenga lo svolgimento del problema proposto commentato e affiancato da disegni esplicativi e la risposta alle varie domande riportate nel tema. Qualcosa sono riuscita a fare, e vi chiedo la cortesia di darmi conferma sulla correttezza. Per il resto invece vi chiedo un aiuto
Il testo:

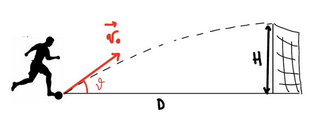
Un calciatore si trova a distanza d (20 m) dalla porta e calcia la palla puntando l’incrocio dei pali. L’angolo che si viene a formare con la direzione perpendicolare alla porta è $alpha$ 45°.
1. Calcolare (in funzione delle grandezze note), attraverso le formule relative ai triangoli rettangoli la
distanza orizzontale che la palla deve percorrere (la indicheremo con D).

A questa ho risposto così: dato che $d$ e $D$ rappresentano rispettivamente un cateto e l'ipotenusa di un triangolo rettangolo, e $alpha$ l'angolo compreso tra i due, la distanza $D$ si calcola come rapporto tra $d$ e $cosalpha$, quindi $D= d / cosalpha = 20 cdot 2 / sqrt(2) = 40 cdot sqrt (2) / 2 m $ (ho razionalizzato)

È corretto?

Prosegue così:

Per effettuare un tiro efficacie il calciatore vorrebbe che la palla raggiungesse l’altezza massima proprio nel
momento in cui entra in porta.


2. Ricava il tempo che la palla impiega a raggiungere il punto dell’incrocio dei pali dall’equazione della
velocità (lungo l’asse y) e sostituisci l’espressione nell’equazione della posizione rispetto all’asse x
(che indichiamo con D) per ottenere $D= (v_(0x) cdot v_(0y)) / g$

Qui ho fatto un tentativo ma non sono riuscita ad arrivare all'espressione $D= (v_(0x) cdot v_(0y)) / g$.
Mio tentativo, partendo dalle leggi orarie del moto parabolico:
$Y=-1/2 g t^2 + v_(0y) t$
$H=-1/2 g t^2 + v_(0y) t$
$t ( 1/2 g t - v_(0y)) = -H $
$ t = -H $ soluzione non accettabile in quanto il tempo non può essere negativo
$ t = 2 cdot (v_(0y) - H) / g $ soluzione accettabile

Sostituisco quest'ultima nell'espressione della posizione rispetto all'asse X $ X = v_(0x) cdot t $ e ottengo:
$ D = v_(x) cdot 2 cdot (v_(0y) - H) / g $
E qui mi sono fermata. Come ci arrivo a $D= (v_(0x) cdot v_(0y)) / g$ ?

3. Ricava l’altezza massima in funzione della componente y della velocità.

Qui ho risposto così: $ H = (v_(0y))^2 / (2g) $
È corretto?

Infine:

4) Ricava l’angolo $theta$ dall’ultima espressione ricavata dopo aver sostituito opportune formule per le
componenti della velocita e aver ricavato $tantheta = sintheta / costheta$ in funzione di H e D.
(H è un dato empirico che si ricava misurando una porta da calcio mentre D lo abbiamo ricavato
nel punto 1 sapendo che d = 20m e α = 45°).
Concludi l’elaborato con un tuo commento sull’angolo appena ricavato osservando le grandezze dalle quali
dipende l’angolo $theta$.

Per questa sono proprio nel pallone
L'elaborato è lungo mi spiace ma questo mi è toccato
Grazie a chiunque vorrà aiutarmi!

[mgrau]

Il punto più alto della traiettoria s raggiunge quando la velocità verticale si azzera, ossia $t = v_(0y)/g$.
In questo tempo, la distanza percorsa è $D = v_(0x)*t = (v_(0y)*v_(0x))/g$

[iolanda.disimone]

Scusami ma non capisco come fai a ottenere $t=(v_(0y))/g$? Se nel punto più alto la componente verticale è nulla, $v_(0y)$ dovrebbe essere $0$ giusto?

[mgrau]

"kyoko": $v_(0y)$ dovrebbe essere $0$ giusto?

$v_y$ è zero nel punto più alto, certo, ma $v_(0y)$ è la componente verticale della velocità iniziale. E siccome la componente verticale della velocità diminuisce di $g$ m/s ogni secondo, diventa zero dopo $v_(0y)/g$ secondi

[iolanda.disimone]

"mgrau":[quote="kyoko"] $v_(0y)$ dovrebbe essere $0$ giusto?

$v_y$ è zero nel punto più alto, certo, ma $v_(0y)$ è la componente verticale della velocità iniziale. E siccome la componente verticale della velocità diminuisce di $g$ m/s ogni secondo, diventa zero dopo $v_(0y)/g$ secondi[/quote]

Tutto chiaro, grazie!
Per quanto riguarda i punti 1), 3) e 4) cosa mi dici? I miei tentativi sono corretti? Il punto 4) non ci ho proprio provato, non so da dove iniziare.

[mgrau]

1) e 3), ok
Per 4), devi pensare che $v_(0y)/v_(0x) = tan theta$; $v_(0y)$ lo ricavi da $H = v_(0y)^2/(2g)$, conoscendo $H$; poi $v_(0x)$ lo dicavi da $D = (v_(0x)v_(0y))/g$, conoscendo $D$

[iolanda.disimone]

Ok, vediamo se ho capito bene.

$tan theta = v_(0y) / v_(0x)$

$H = v_(0y)^2 / (2g) = 2,44 m $
H = 2,44 m come dato l'ho trovato online, il professore nel testo ha scritto che "H è un dato empirico che si ricava misurando una porta da calcio" ma io ho preferito cercare su google

Da questa ricavo che
$v_(0y)^2 = 2,44 cdot 2g$
$v_(0y) = sqrt (47,824)= 6,9 m/s$

Per quanto riguarda la componente orizzontale, avendo
$D = (v_(0x) cdot v_(0y)) / g = 28,28 m $
ottengo
$v_(0x)=(28,28 cdot 9,8) / (6,9) = 40 m/s$

Quindi $tan theta = v_(0y) / v_(0x) = (6,9) / 40 = 0,17 $
$theta = arctan (0,17) = 9,64°$

Che ne pensi?

[mgrau]

[iolanda.disimone]

Perfetto grazie mille sei stato davvero gentilissimo (e chiarissimo).

[iolanda.disimone]

"mgrau"::smt023

Scusami mi è venuto un altro dubbio...
nel calcolo dell'altezza massima H, forse il professore vorrebbe che ci arrivassi con vari passaggi e non scrivendo semplicemente la formula nota...
Così ho scritto:
$H = 1/2 g t^2 + v_(0y) cdot t + y_0$
Sostituisco a t l'espressione precedentemente trovata $t= v_(0y) /g$
e ottengo
$H = 1/2 g (v_(0y) / g)^2 + v_(0y) cdot v_(0y)/g + 0$
$H = (v_(0y)^2 / (2g)) + v_(0y)^2 / g$

Perché non viene?

[mgrau]

C'è un problema di segni. Se scegli l'asse y diretto in alto, hai $v_(0y) > 0$, ma allora devi prendere $g$ negativo. così ti viene $H = -1/2 g (v_(0y) / g)^2 + v_(0y) cdot v_(0y)/g = v_(0y)^2/(2g)$

Se poi lo vedi graficamente, con un diagramma v/t, in cui le aree rappresentano lo spazio percorso, è ancora più evidente

[iolanda.disimone]

Che sciocca, non ci avevo pensato! Grazie ancora