Accelerazione in un sistema di carrucole e pesetti
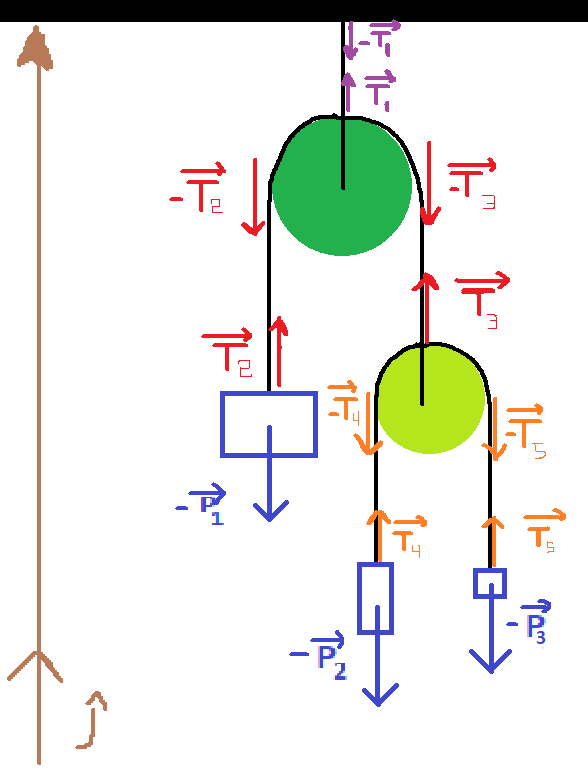
Inserisco l'immagine descrittiva dell'esercizio nello spoiler perché di estensione piuttosto invadente 
Naturalmente comprensiva della mia idea di come dovrebbero andare le cose:
In particolare riporto la consegna dell'esercizio:
"Dati $m_1=2.5Kg, m_2=1.8 Kg$ e $m_3=2.2 Kg$, calcolare le accelerazioni delle
masse e le tensioni delle funi. (Funi e carrucole sono ideali)."
Queste sono le mie considerazioni: Il filo che passa sulla carrucola verde chiaro è unico, ideale e continuo per cui la tensione è una costante ed è pertanto uguale ovunque. Motivo per cui $T_4 = T_5$ e chiamerò questa d'ora in avanti $T'$. Analoga considerazione ho mosso nei confronti della carrucola verde scuro per cui nel risolvere ho considerato $T_2=T_3$ indicata come $T$. Applicando il secondo principio della dinamica alle due carrucole ottengo nell'ordine che $T = 2T'$
A questo punto applico il secondo principio della dinamica ai pesetti $2$ e $3$ ottenendo rispettivamente che
$T'-m_2g = m_2a_2$
$T'-m_3g = m_3a_3$
Applicando il secondo principio al pesetto $1$ ottengo invece che
$2T' -m_1g = m_1a_1$
A questo punto ho pensato che il filo ideale sulla carrucola in basso ponesse un vincolo cinematico sul modulo dell'accelerazione dei pesetti $2$ e $3$ che dovranno quindi essere uguali. In particolare l'accelerazione di uno sarà in verso opposta alla rimanente. Ad esempio scelgo di porre che il pesetto $2$ salga verso l'alto mentre $3$ scenda. Chiamando $a_23$ l'accelerazione comune si scrive che:
\(\begin{cases} T'-m_2g = m_2a_{23} \\ T'-m_3g = -m_3a_{23} \end{cases} \implies \begin{cases} T' =m_2(g +a_{23}) \\ (m_2-m_3)g = -(m_2+m_3)a_{23} \end{cases} \implies a_{23} = \frac{m_3-m_2}{m3+m2}g\)
da cui ricaverei anche che $T' = m_2(1+\frac{m_3-m_2}{m_3+m_2})g$
A questo punto $a_1 = 2\frac{m_2}{m_1}(\frac{m_3-m_2}{m_3+m_2})$ mentre $T = 2m_2(1+\frac{m_3-m_2}{m_3+m_2})g$
Inultile dire che con i calcoli che ho attuato i risultati sono sbagliati. Cosa mi sono perso? Addirittura pare che $a_3 \ne a_2$ bah...
Naturalmente comprensiva della mia idea di come dovrebbero andare le cose:
In particolare riporto la consegna dell'esercizio:
"Dati $m_1=2.5Kg, m_2=1.8 Kg$ e $m_3=2.2 Kg$, calcolare le accelerazioni delle
masse e le tensioni delle funi. (Funi e carrucole sono ideali)."
Queste sono le mie considerazioni: Il filo che passa sulla carrucola verde chiaro è unico, ideale e continuo per cui la tensione è una costante ed è pertanto uguale ovunque. Motivo per cui $T_4 = T_5$ e chiamerò questa d'ora in avanti $T'$. Analoga considerazione ho mosso nei confronti della carrucola verde scuro per cui nel risolvere ho considerato $T_2=T_3$ indicata come $T$. Applicando il secondo principio della dinamica alle due carrucole ottengo nell'ordine che $T = 2T'$
A questo punto applico il secondo principio della dinamica ai pesetti $2$ e $3$ ottenendo rispettivamente che
$T'-m_2g = m_2a_2$
$T'-m_3g = m_3a_3$
Applicando il secondo principio al pesetto $1$ ottengo invece che
$2T' -m_1g = m_1a_1$
A questo punto ho pensato che il filo ideale sulla carrucola in basso ponesse un vincolo cinematico sul modulo dell'accelerazione dei pesetti $2$ e $3$ che dovranno quindi essere uguali. In particolare l'accelerazione di uno sarà in verso opposta alla rimanente. Ad esempio scelgo di porre che il pesetto $2$ salga verso l'alto mentre $3$ scenda. Chiamando $a_23$ l'accelerazione comune si scrive che:
\(\begin{cases} T'-m_2g = m_2a_{23} \\ T'-m_3g = -m_3a_{23} \end{cases} \implies \begin{cases} T' =m_2(g +a_{23}) \\ (m_2-m_3)g = -(m_2+m_3)a_{23} \end{cases} \implies a_{23} = \frac{m_3-m_2}{m3+m2}g\)
da cui ricaverei anche che $T' = m_2(1+\frac{m_3-m_2}{m_3+m_2})g$
A questo punto $a_1 = 2\frac{m_2}{m_1}(\frac{m_3-m_2}{m_3+m_2})$ mentre $T = 2m_2(1+\frac{m_3-m_2}{m_3+m_2})g$
Inultile dire che con i calcoli che ho attuato i risultati sono sbagliati. Cosa mi sono perso? Addirittura pare che $a_3 \ne a_2$ bah...
Risposte
Nessuna idea?
Orientando l'asse verticale complessivamente verso l'alto, $m_2$ e $m_3$ hanno accelerazioni relative opposte:
Per determinare le accelerazioni:
Il fatto che:
è senz'altro di buon auspicio.
1. $m_1a_1=-m_1g+T_1$
2. $m_2a_2=-m_2g+T_2$
3. $m_3a_3=-m_3g+T_2$
4. $T_1=2T_2$
5. $a_2+a_1=-a_3-a_1$
Per determinare le accelerazioni:
$[a_1=(2m_2a_2-m_1g+2m_2g)/m_1] ^^ [a_3=(m_2a_2+m_2g-m_3g)/m_3] rarr$
$rarr a_2=(-m_1m_2+3m_1m_3-4m_2m_3)/(m_1m_2+m_1m_3+4m_2m_3)g=-48/323g$
Il fatto che:
$[m_1=m_2+m_3] ^^ [m_2=m_3] rarr [a_1=a_2=a_3=0]$
è senz'altro di buon auspicio.
In questo caso come si spiega che il filo ideale e quindi inestensibile non costituisca un vincolo tra $a_2$ ed $a_3$?
Veramente, il vincolo cinematico di cui parli è proprio quello per cui $m_2$ e $m_3$ devono avere accelerazioni relative opposte:
Si tratta del solito vincolo cinematico imposto sulle accelerazioni relative piuttosto che su quelle assolute.
$a_2+a_1=-a_3-a_1$
Si tratta del solito vincolo cinematico imposto sulle accelerazioni relative piuttosto che su quelle assolute.
Ho compreso il motivo adesso, non avevo considerato di imporre la condizione sulla lunghezza dei fili! Grazie.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo