Integrale statistica di bose
Salve, avrei un problema con un integrale. So bene che la soluzione all integrale :
Il mio problema consiste però nel trovare una primitiva di quella funzione in caso gli estremi di integrazione non siano quelli detti.
Ad esempio
ne approfitto per chiedere dove posso trovare una dimostrazione della prima uguaglianza, per ogni esponente di $t$.
La cosa mi interessa molto visto che se si affronta la statistica di Bose e si vuole calcolare medie su osservabili, si è spesso davanti a quel genere di integrale.
$ int_{0}^{\infty} frac{t}{\e^{t] -1} = \gamma(2) \zeta(2) $
Il mio problema consiste però nel trovare una primitiva di quella funzione in caso gli estremi di integrazione non siano quelli detti.
Ad esempio
$ int_{-1}^{2}frac{t}{e^t-1}dt $
ne approfitto per chiedere dove posso trovare una dimostrazione della prima uguaglianza, per ogni esponente di $t$.
La cosa mi interessa molto visto che se si affronta la statistica di Bose e si vuole calcolare medie su osservabili, si è spesso davanti a quel genere di integrale.
Risposte
"Pepermatt94":
Il mio problema consiste però nel trovare una primitiva di quella funzione in caso gli estremi di integrazione non siano quelli detti.
Ad esempio
$ int_{-1}^{2}frac{t}{e^t-1}dt $
Dunque, se posti un messaggio in Analisi superiore immagino che tu abbia molte più conoscenze matematiche di me, che non sono affatto un Matematico ma piuttosto un "Empirico"[nota]del resto ho fatto Ragioneria alle superiori...[/nota].
La funzione che vuoi cercare di integrare, come dovrebbe esserti noto, non ha una primitiva esprimibile elementarmente....quindi per risolvere quell'integrale ci sono diverse vie ma che dovresti già aver visto nel tuo precedente corso di studi....tutto sommato non mi pare un quesito da Analisi Superiore...
Io, da empirico, faccio così[nota]questo metodo si chiama "Importance Sampling"[/nota]:
1) mi scelgo una funzione "facile" che assomigli alla funzione integranda $p(x)=x/(e^x-1)$; senza troppe pretese, mi scelgo $e^(-x/2)$
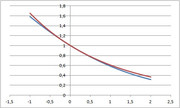
come vedi non è malaccio... un po' più bassa da una parte, un po' più alta dall'altra, sempre decrescente, stessa concavità....CONTINUA su tutto l'intervallo (che non guasta mai), facilissima da integrare...
2) faccio in modo che la mia funzione approssimante sia una densità di probabilità nell'intervallo che mi interessa...facile, impongo
$kint_(-1)^(2)e^(-x/2)dx=1$ ed ottengo subito
$f_X(x)=e/(2(esqrt(e)-1))e^(-x/2)$
3) Mi calcolo la sua funzione di distribuzione:
$F_X(x)=e/(esqrt(e)-1)[sqrt(e)-e^(-x/2)]=y$
4) Invoco il teorema della Trasformazione integrale (sempre sia lodato
$x=-log[sqrt(e)-(esqrt(e)-1)/e y]^2$
5) a questo punto, so che la $y$ è una uniforme in $[0;1]$...non mi resta che generare casualmente un campione di ampiezza $n$ dalla uniforme (lo fa qualunque calcolatrice, anche tascabile.....io ho usato Excel) e il mio integrale sarà la media empirica dei valori $(p(x))/(f(x))$
Nell'esempio in esame, l'integrale calcolato con un appostito software mi ha dato 2.491399. Io ho estratto 1000 numeri casuali per 10 volte con i seguenti risultati
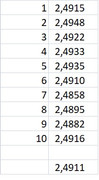
...dire che ci siamo

La ringrazio molto e trovo fantastico il fatto che è un empirico. Ho postato in analisi superiore in realtà perchè non sapevo bene dove postare. Se si può spostare sposto subito. Sono uno studente al terzo anno di fisica. Sto affrontando un minimo di importance sampling nel corso di probabilità, ma solo un accenno. Le volevo chiedere solo un ulteriore spiegazione sul punto 5, che mi sembra il più numerico, non ho capito su cosa media.
L'idea dell'importance sampling è molto intuitiva:
Per calcolare $int_(mathcal(D)) p(x) dx$ lo si trasforma in $int_(mathcal(D)) (p(x))/(f(x)) f(x)dx=mathbb{E}[( p(x))/(f(x)) ]$
Quindi, per motivazioni statistiche ben note, si può approssimare la media vera con la media empirica (media osservata)
$mathbb{E}[( p(x))/(f(x)) ]~~1/n sum_(x=1)^(n)(p(x))/(f(x)) $
I valori $x=F^(-1)(y)$ sono ricavati dai numeri $y_1,...,y_n$ generati casualmente (col calcolatore) da una distribuzione uniforme su $[0;1]$
Tutto il trucco sta nel fatto che, con qualunque distribuzione continua $F_ X(x)$ , sai che $Y=F_ X(x)$ si distribuisce come una uniforme su $[0;1]$
Riprendendo l'esempio ecco la tabellina fatta con 10 numeri casuali
(click me!)
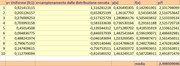
Ovviamente la stima non è un granché, la velocità di convergenza dell'Importance Sampling è piuttosto lenta. E' comunque possibile calcolare l'incertezza statistica sul calcolo dell'integrale operando come di consueto clacolando l'errore standard della media stimata: $(hat(sigma)_(p/f))/sqrt(n)$
Nel post precedente ho fatto 10 estrazioni da 1000 numeri casuali ciascuna e poi ho fatto anche la media delle 10 medie, che rappresenta una stima con un'estrazione di 10.000 numeri casuali...la lentezza di convergenza non è un problema, dato che le estrazioni si fanno col calcolatore.....
Ora dovrebbe essere chiaro
Per spostare il topic lo deve fare il moderatore della stanza o un moderatore globale, se lo ritiene necessario ... io sono di un'altra parrocchia, non ho poteri qui...
Per calcolare $int_(mathcal(D)) p(x) dx$ lo si trasforma in $int_(mathcal(D)) (p(x))/(f(x)) f(x)dx=mathbb{E}[( p(x))/(f(x)) ]$
Quindi, per motivazioni statistiche ben note, si può approssimare la media vera con la media empirica (media osservata)
$mathbb{E}[( p(x))/(f(x)) ]~~1/n sum_(x=1)^(n)(p(x))/(f(x)) $
I valori $x=F^(-1)(y)$ sono ricavati dai numeri $y_1,...,y_n$ generati casualmente (col calcolatore) da una distribuzione uniforme su $[0;1]$
Tutto il trucco sta nel fatto che, con qualunque distribuzione continua $F_ X(x)$ , sai che $Y=F_ X(x)$ si distribuisce come una uniforme su $[0;1]$
Riprendendo l'esempio ecco la tabellina fatta con 10 numeri casuali
(click me!)

Ovviamente la stima non è un granché, la velocità di convergenza dell'Importance Sampling è piuttosto lenta. E' comunque possibile calcolare l'incertezza statistica sul calcolo dell'integrale operando come di consueto clacolando l'errore standard della media stimata: $(hat(sigma)_(p/f))/sqrt(n)$
Nel post precedente ho fatto 10 estrazioni da 1000 numeri casuali ciascuna e poi ho fatto anche la media delle 10 medie, che rappresenta una stima con un'estrazione di 10.000 numeri casuali...la lentezza di convergenza non è un problema, dato che le estrazioni si fanno col calcolatore.....
Ora dovrebbe essere chiaro
Per spostare il topic lo deve fare il moderatore della stanza o un moderatore globale, se lo ritiene necessario ... io sono di un'altra parrocchia, non ho poteri qui...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo