Analisi singolarità (+ calcolo integrale con metodo dei residui)
Salve, avrei bisogno di un chiarimento per il seguente esercizio:
Dopo aver classificato le singolarità al finito della funzione complessa di variabile complessa $f(z) = \frac {z^2-1}{(z-2)^4 (4z-1) (1+cos (pi z))} $, si calcoli l’integrale di linea $ \oint_{\Gamma} f(z) dz$ dove $ \Gamma = {z \in CC :\abs z = 1 }$
Si ha un polo di 4° ordine in $z=2$ -che non verrà preso in considerazione nel calcolo dell'integrale in quanto al di fuori della circonferenza data- e un polo di 1° ordine in $z=1/4$.
Inoltre, $(1+cos (pi z) )$ si annulla per $z=2k+1, k \in ZZ$, e consideriamo solo $z=+-1$, per lo stesso motivo di cui sopra.
Ora, dal momento che $z=+-1$ è sia un polo che uno zero di primo ordine per $f(z)$, è sufficiente per affermare che è sono punti di singolarità eliminabile? Oppure è necessario provvedere al calcolo del limite?
In quest'ultimo caso, avrei bisogno di una mano, perché non riesco a svolgerlo.
Dopo aver classificato le singolarità al finito della funzione complessa di variabile complessa $f(z) = \frac {z^2-1}{(z-2)^4 (4z-1) (1+cos (pi z))} $, si calcoli l’integrale di linea $ \oint_{\Gamma} f(z) dz$ dove $ \Gamma = {z \in CC :\abs z = 1 }$
Si ha un polo di 4° ordine in $z=2$ -che non verrà preso in considerazione nel calcolo dell'integrale in quanto al di fuori della circonferenza data- e un polo di 1° ordine in $z=1/4$.
Inoltre, $(1+cos (pi z) )$ si annulla per $z=2k+1, k \in ZZ$, e consideriamo solo $z=+-1$, per lo stesso motivo di cui sopra.
Ora, dal momento che $z=+-1$ è sia un polo che uno zero di primo ordine per $f(z)$, è sufficiente per affermare che è sono punti di singolarità eliminabile? Oppure è necessario provvedere al calcolo del limite?
In quest'ultimo caso, avrei bisogno di una mano, perché non riesco a svolgerlo.
Risposte
Visto che $+-1$ sono zeri dello stesso ordine per numeratore e denominatore di $f$, tali punti risultano singolarità eliminabili "per compensazione". Quindi non ti serve calcolare nulla. 
P.S.: E comunque, per il calcolo di quel limite serve conoscere solo i limiti notevoli... Roba da Analisi I.
P.S.: E comunque, per il calcolo di quel limite serve conoscere solo i limiti notevoli... Roba da Analisi I.
Grazie per la risposta; mmh, ad Analisi 1 me la cavavo, ma suppongo che mi stia sfuggendo qualcosa 
Ti spiacerebbe illuminarmi, senza che creo un altro post nella sezione apposita?
Ti spiacerebbe illuminarmi, senza che creo un altro post nella sezione apposita?
Scusa, guardando attentamente hai sbagliato a classificare lo zero del denominatore.
Infatti, $1 + cos(pi z) $ si azzera in $2k + 1$ insieme alla sua derivata prima, che è $-pi sin(pi z)$, ergo tali punti sono zero del denominatore d'ordine $2$; quindi i punti $+-1$ sono poli del primo ordine per $f$.
Infatti, $1 + cos(pi z) $ si azzera in $2k + 1$ insieme alla sua derivata prima, che è $-pi sin(pi z)$, ergo tali punti sono zero del denominatore d'ordine $2$; quindi i punti $+-1$ sono poli del primo ordine per $f$.
La sua derivata prima $-pi sin (pi z) $ si azzera in $k$ se non erro; a questo punto, devo considerarlo di secondo ordine anche se $z=+-1$ si ottiene per valori di $k$ differenti, oppure no?
Perché l'analisi dei residui secondo wolfram non mi segnala nessun polo in $+-1$:
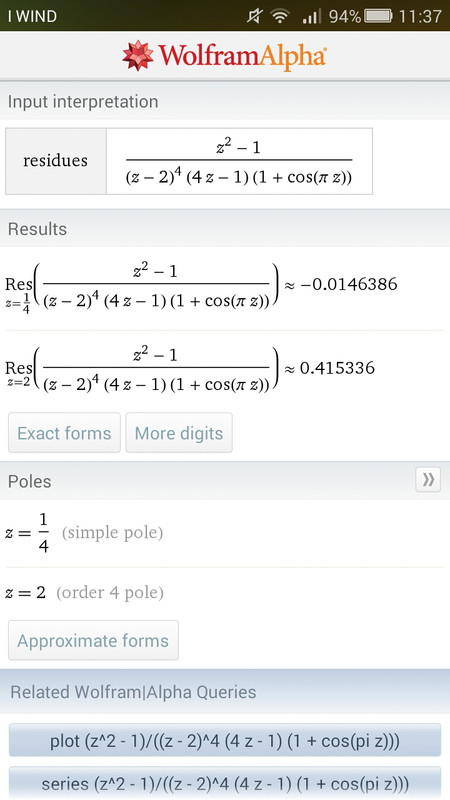
EDIT: Rifacendo i calcoli mi risulta effettivamente che sia un polo di secondo ordine, forse è una qualche limitazione di wolfram non so.
A questo punto quale risultato mi viene in aiuto per il calcolo del residuo in $+-1$ ?
Perché l'analisi dei residui secondo wolfram non mi segnala nessun polo in $+-1$:

EDIT: Rifacendo i calcoli mi risulta effettivamente che sia un polo di secondo ordine, forse è una qualche limitazione di wolfram non so.
A questo punto quale risultato mi viene in aiuto per il calcolo del residuo in $+-1$ ?
Lascia perdere wolfram e ragiona con la tua testa.
La derivata prima di $1 + cos(pi z)$ si annulla in tutti i numeri interi, in particolare sui numeri dispari; ergo $+-1$ sono zeri del secondo ordine per $1 + cos(pi z)$ (così come tutti i numeri dispari).
Tuttavia i punti $+- 1$ sono poli solo del primo ordine per $f$, giacché essi vengono parzialmente compensati nell’ordine da zeri del numeratore.
Il residuo in tali punti si può calcolare coi limiti notevoli od usando bene il teorema di de l’Hôpital. Insomma, ad esempio hai:
\[
\begin{split}
\operatorname{Res}(f; 1) &= \lim_{z\to 1} (z-1) f(z) \\
&= \lim_{z\to 1} \frac{(z + 1) (z - 1)^2}{(z - 2)^4 (4z - 1) (1 + \cos \pi z)}\\
& \stackrel{w = z-1}{=} \lim_{w \to 0} \frac{(w + 2) w^2}{(w - 1)^4 (4w + 3) (1 - \cos \pi w)}\\
&= \cdots
\end{split}
\]
col risultato che si trova coi limiti notevoli.
La derivata prima di $1 + cos(pi z)$ si annulla in tutti i numeri interi, in particolare sui numeri dispari; ergo $+-1$ sono zeri del secondo ordine per $1 + cos(pi z)$ (così come tutti i numeri dispari).
Tuttavia i punti $+- 1$ sono poli solo del primo ordine per $f$, giacché essi vengono parzialmente compensati nell’ordine da zeri del numeratore.
Il residuo in tali punti si può calcolare coi limiti notevoli od usando bene il teorema di de l’Hôpital. Insomma, ad esempio hai:
\[
\begin{split}
\operatorname{Res}(f; 1) &= \lim_{z\to 1} (z-1) f(z) \\
&= \lim_{z\to 1} \frac{(z + 1) (z - 1)^2}{(z - 2)^4 (4z - 1) (1 + \cos \pi z)}\\
& \stackrel{w = z-1}{=} \lim_{w \to 0} \frac{(w + 2) w^2}{(w - 1)^4 (4w + 3) (1 - \cos \pi w)}\\
&= \cdots
\end{split}
\]
col risultato che si trova coi limiti notevoli.
"gugo82":
\[
\begin{split}
\operatorname{Res}(f; 1) &= \lim_{z\to 1} (z-1) f(z) \\
&= \lim_{z\to 1} \frac{(z + 1) (z - 1)^2}{(z - 2)^4 (4z - 1) (1 + \cos \pi z)}\\
& \stackrel{w = z-1}{=} \lim_{w \to 0} \frac{(w + 2) w^2}{(w - 1)^4 (4w + 3) (1 - \cos \pi w)}\\
&= \cdots
\end{split}
\]
$lim_{w\to 0} frac{(w + 2) pi^2 w^2}{pi^2(w - 1)^4 (4w + 3) (1 - \cos \pi w)} = lim_{w\to 0} frac{2 (w + 2) }{pi^2(w - 1)^4 (4w + 3) } = frac{4}{3pi^2}$ dove si è usato
$lim_{f(w)\to 0} frac{1-cos(f(w))} {(f(w))^2} = 1/2 $
Ok, non credo ci siano ulteriori difficoltà nel proseguimento dell'esercizio, grazie mille


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo