Proprietà potenza di potenza
se è vera questa proprietà
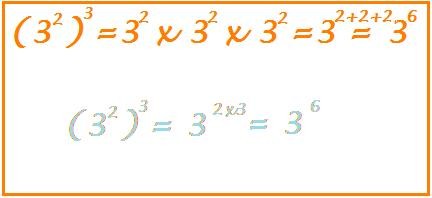
come mai non vale anche se c'è un incognita.
Esempio:
$e^({x-sqrt2}^2)=e^(2{x-sqrt2})$
se sostituisco 0
$e^2=e^(2{-sqrt2})$

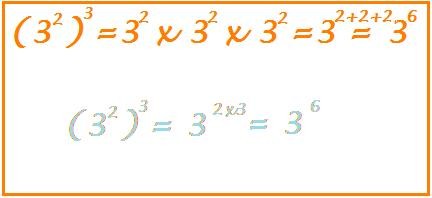
come mai non vale anche se c'è un incognita.
Esempio:
$e^({x-sqrt2}^2)=e^(2{x-sqrt2})$
se sostituisco 0
$e^2=e^(2{-sqrt2})$
Risposte
Le potenze si leggono e si valutano a partire dall'ultimo apice, cioè dall'ultimo "numerino" scritto in alto.
Es:
$x=10^(9^(8^(7^(6^(5^(4^(3^(2))))))))$.
Prima si valuta $k_1=3^2$
poi $k_2=4^(k_1)$
poi $k_3=5^(k_2)$
e così via....
a meno che non ci siano delle parentesi, allora le parentesi hanno la precedenza su ogni altro calcolo.
Es:
$x=10^(9^(8^(7^(6^(5^(4^(3^(2))))))))$.
Prima si valuta $k_1=3^2$
poi $k_2=4^(k_1)$
poi $k_3=5^(k_2)$
e così via....
a meno che non ci siano delle parentesi, allora le parentesi hanno la precedenza su ogni altro calcolo.
"Quinzio":
a meno che non ci siano delle parentesi, allora le parentesi hanno la precedenza su ogni altro calcolo.
cioè?
Prova a pensarci... il problema è che non capisci il significato della frase o non sai come usare le parentesi ?
Come calcoli questo ?
$x=(10^(9^(8^(7^6))))^(5^(4^(3^2)))$.
Come calcoli questo ?
$x=(10^(9^(8^(7^6))))^(5^(4^(3^2)))$.
"Quinzio":
Come calcoli questo ?
$x=(10^(9*8*7*6))^(5*4*3*2)$
No (anche perchè non fai chiarezza)
"Quinzio":
No (anche perchè non fai chiarezza)
fuori la parentesi:
1)$(2*(3))$
2)$((2*3)*4)$
3)$((2*3*4)*5)$
dentro la parentesi:
1)$(6*(7))$
2)$((6*7)*8)$
3)$((6*7*8)*9)$
va meglio?
Quinzio è stato sin troppo chiaro, ma a quanto pare...
Una cosa è scrivere
\[(a^b)^c\]
e un'altra è scrivere
\[a^{b^c}\]
Facciamo un esempio, con $a=4$, $b=3$ e $c=2$. Hai
\[(4^3)^2=4^{3\cdot 2} =4^6=\text{(non ho idea di quanto faccia, usa la calcolatrice)}\]
Invece
\[4^{3^2}=4^{9}=\text{(alzo le mani anche qui...)}\]
Ok?
Una cosa è scrivere
\[(a^b)^c\]
e un'altra è scrivere
\[a^{b^c}\]
Facciamo un esempio, con $a=4$, $b=3$ e $c=2$. Hai
\[(4^3)^2=4^{3\cdot 2} =4^6=\text{(non ho idea di quanto faccia, usa la calcolatrice)}\]
Invece
\[4^{3^2}=4^{9}=\text{(alzo le mani anche qui...)}\]
Ok?
"Plepp":
Ok?
grazie a te e a quinzio per la pazienza



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo