Limite...
secondo voi il limite tende ad infinito ??
spero di si
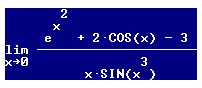
spero di si
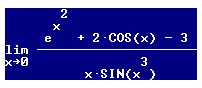
Risposte
Se non ho scritto male la funzione, il grafico nei pressi di 0 è :
Bye.
Bye.
Si puo' scrivere cosi'(ometto x-->0):
lim(e^(x^2)+2cos(x)-3)/[x^4*sin(x^3)/(x^3)]
Ora lim(sin(x^3)/(x^3))=1 e pertanto si ha:
lim(e^(x^2)+2cos(x)-3)/(x^4)
Applicando piu' volte l'Hopital ( o facendo
uso di sviluppi in serie opportunamente
troncati) si vede che il limite e' 7/12.
karl.
lim(e^(x^2)+2cos(x)-3)/[x^4*sin(x^3)/(x^3)]
Ora lim(sin(x^3)/(x^3))=1 e pertanto si ha:
lim(e^(x^2)+2cos(x)-3)/(x^4)
Applicando piu' volte l'Hopital ( o facendo
uso di sviluppi in serie opportunamente
troncati) si vede che il limite e' 7/12.
karl.
mm va beh allora l'ho sbagliato...
io ho usato i limiti notevoli nel risolverlo, perchè con l'hopital nno finiva mai la cosa...o cmq usciva un bel pò di roba...
io ho usato i limiti notevoli nel risolverlo, perchè con l'hopital nno finiva mai la cosa...o cmq usciva un bel pò di roba...
ma non si può fare usando i limiti del tipo (e^x-1)/x -->1 e sinx/x -->1 ?
Ci ho provato ma non se ne esce ,a meno
di particolari acrobazie che personalmente
non vedo.
Forse qualche altro.
Saluti da karl.
di particolari acrobazie che personalmente
non vedo.
Forse qualche altro.
Saluti da karl.
Ok grazie lo stesso Karl
Questo limite era banale risolverlo con Taylor:
e^(x^2)=x^4/2 + x^2 + 1 + O(x^6)
cos(x)=x^4/24 - x^2/2 + 1 + O(x^6)
sin(x)=x^3 + O(x^6)
Il tutto diventava
numeratore
x^4/2 + x^2 + 1 + O(x^6) + 2(x^4/24 - x^2/2 + 1 + O(x^6))-3 = x^4/2 + x^4/12 + O(x^6)
denominatore
x*x^3 + O(x^6) = x^4 + O(x^7)
Dunque
1/2 + 1/12 = 7/12
e^(x^2)=x^4/2 + x^2 + 1 + O(x^6)
cos(x)=x^4/24 - x^2/2 + 1 + O(x^6)
sin(x)=x^3 + O(x^6)
Il tutto diventava
numeratore
x^4/2 + x^2 + 1 + O(x^6) + 2(x^4/24 - x^2/2 + 1 + O(x^6))-3 = x^4/2 + x^4/12 + O(x^6)
denominatore
x*x^3 + O(x^6) = x^4 + O(x^7)
Dunque
1/2 + 1/12 = 7/12
mm grazie pachito...
ok il limite era giusto quello risolto da Pachito...
cmq avrei un'altra domanda...se invece che tendere a 0 fosse stato all'infinito si sarebbe potuto risolvere lo stesso con Taylor...e se si ,come ?
cmq avrei un'altra domanda...se invece che tendere a 0 fosse stato all'infinito si sarebbe potuto risolvere lo stesso con Taylor...e se si ,come ?
Non si può usare Taylor, ad esempio sen(x) tende a x solo per x-->0. Se x-->+inf sen(x) è indeterminato.
Poi comunque usare gli ordini di grandezza.
WonderP.
Poi comunque usare gli ordini di grandezza.
WonderP.
ok grazie wonder!
Taylor , se applicabile, approssima una funzione bene quanto vuoi in un intorno di un punto.
Se il punto è all'infinito, quello che si fa è il classico isomorfismo x=1/y e ciò che sta ad infinito va a 0 e viceversa.
Es.
lim x*sin(1/x) = 1
x->inf
Se il punto è all'infinito, quello che si fa è il classico isomorfismo x=1/y e ciò che sta ad infinito va a 0 e viceversa.
Es.
lim x*sin(1/x) = 1
x->inf
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo