Interpretazione Teorema di Lagrange...
allora non riesco a capire dal mio libro un aspetto di questo teorema, ovvero, se considero i punti all'estremo dell' intervallo [a,b] avrei che la derivata o è minore o è maggiore di 0 essendo che posso considerare incrementi o solo positivi o solo negativi rispetto ad a e b... comunque studiando nel passato ero sicuro che qui non si potesse effettuare nessun calcolo che permettesse di definire la derivata, proprio perchè il rapporto incrementale risulta o maggiore o minore di 0... ma leggendo il libro credo di non aver capito assolutamente niente, o meglio che anche se non si riesce nel definire una derivata che sia soltanto uguale a 0 vale comunque il teorema di Lagrange 
... ho interpretato male il significato di quello che c'è scritto oppure è proprio così anche se mi pare una cosa assurda?...
... ho interpretato male il significato di quello che c'è scritto oppure è proprio così anche se mi pare una cosa assurda?...
Risposte
Non ho capito quasi niente di quello che hai scritto.
Teorema: Sia $f: [a,b] -> RR$ , continua in $[a,b]$ e derivabile nell'aperto. Allora $EE xi in ] a , b [$ tale che $f'(xi) = (f(b) - f(a))/(b - a)$.
Il teorema di Lagrange dice questo e basta. Nulla di più, nulla di meno. Considerato l'enunciato, quali sono i tuoi dubbi?
Teorema: Sia $f: [a,b] -> RR$ , continua in $[a,b]$ e derivabile nell'aperto. Allora $EE xi in ] a , b [$ tale che $f'(xi) = (f(b) - f(a))/(b - a)$.
Il teorema di Lagrange dice questo e basta. Nulla di più, nulla di meno. Considerato l'enunciato, quali sono i tuoi dubbi?
"Seneca":
Non ho capito quasi niente di quello che hai scritto.
Teorema: Sia $f: [a,b] -> RR$ , continua in $[a,b]$ e derivabile nell'aperto. Allora $EE xi in ] a , b [$ tale che $f'(xi) = (f(b) - f(a))/(b - a)$.
Il teorema di Lagrange dice questo e basta. Nulla di più, nulla di meno. Considerato l'enunciato, quali sono i tuoi dubbi?
ammetto di essere stato abbastanza confusionario
... comunque il mio dubbio era se fosse possibile che (da quanto ho interpretato dal libro) il teorema di Lagrange valesse anche per gli estremi dell'intervallo e non solo per i punti interni... mi pare una cosa un pò assurda in quanto le rette passanti per un punto sono infinite e quindi non è possibile calcolare una derivata che sia unica... ma volevo esserne sicuro...
"Ma.Gi.Ca. D":
il teorema di Lagrange valesse anche per gli estremi dell'intervallo e non solo per i punti interni...
Questo è criptico.
"Ma.Gi.Ca. D":
mi pare una cosa un pò assurda in quanto le rette passanti per un punto sono infinite e quindi non è possibile calcolare una derivata che sia unica... ma volevo esserne sicuro...
Un dialetto in voga ai tempi di Nefertiti?
Spiegati meglio.
"Ma.Gi.Ca. D":
[quote="Seneca"]Non ho capito quasi niente di quello che hai scritto.
Teorema: Sia $f: [a,b] -> RR$ , continua in $[a,b]$ e derivabile nell'aperto. Allora $EE xi in ] a , b [$ tale che $f'(xi) = (f(b) - f(a))/(b - a)$.
Il teorema di Lagrange dice questo e basta. Nulla di più, nulla di meno. Considerato l'enunciato, quali sono i tuoi dubbi?
ammetto di essere stato abbastanza confusionario
... comunque il mio dubbio era se fosse possibile che (da quanto ho interpretato dal libro) il teorema di Lagrange valesse anche per gli estremi dell'intervallo e non solo per i punti interni... mi pare una cosa un pò assurda in quanto le rette passanti per un punto sono infinite e quindi non è possibile calcolare una derivata che sia unica... ma volevo esserne sicuro...[/quote]da quello che scrivi pare tu non abbia capito molto il significato del teorema, che visivamente è intuitivo e si può spiegare così:
prendi una funzione$ f(x)$ in un intervallo$ [a,b]$. chiamiamo r la retta passante per $ (a,f(a))$ e $(b,f(b))$. il teorema garantisce che esiste almeno un'altra retta s (quella gialla in figura) parallela ad r e tangente al grafico di $f(x)$ in un punto interno ad [a,b]:
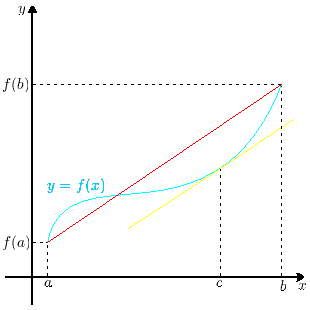
se hai capito questo dovrebbe essere chiaro che il teorema di lagrange si applica ad intervalli e non a singoli punti e quindi la tua domanda è sbagliata in partenza
Se ti può essere utile, il teorema di Lagrange è un caso particolare del teorema di Cauchy, con $g'(x)=1$ ed il teorema di Rolle è un caso particolare del teorema di Lagrange: infatti, se "raddrizzi" il disegno di sopra, cioè fai in modo che $f(a)=f(b)$, intuitivamente osservi che la derivata nel punto interno non può che essere 0. Questi teoremi sono tutti e tre collegati, e non c'è nulla da capire oltre quello che già ti è stato detto. Spiega quali sono i tuoi dubbi in maniera più chiara così possiamo aiutarti meglio. Ciao.
"Seneca":
[quote="Ma.Gi.Ca. D"] il teorema di Lagrange valesse anche per gli estremi dell'intervallo e non solo per i punti interni...
Questo è criptico.
"Ma.Gi.Ca. D":
mi pare una cosa un pò assurda in quanto le rette passanti per un punto sono infinite e quindi non è possibile calcolare una derivata che sia unica... ma volevo esserne sicuro...
Un dialetto in voga ai tempi di Nefertiti?
Spiegati meglio.
[/quote]oddio!
... ok riformulo più semplicisticamente... il teorema di Lagrange può essere applicato anche all'intervallo $[a,b]$ cioè estremi compresi?... come detto prima molto probabilmente ho interpretato male il senso di ciò che è scritto sul libro, però volevo verificare...
Non riesco a capire qual è il tuo problema:-)
Tu non applichi il teorema di Lagrange ad un intervallo. Lo applichi ad una funzione definita su un intervallo (non lo applichi a dei punti, se ho capito bene il senso della tua domanda).
O forse il problema è solo che non capisci se lo $xi$ di cui il teorema predica l'esistenza può trovarsi o meno in uno degli estremi dell'intervallo...
O forse il problema è solo che non capisci se lo $xi$ di cui il teorema predica l'esistenza può trovarsi o meno in uno degli estremi dell'intervallo...
"Seneca":
Tu non applichi il teorema di Lagrange ad un intervallo. Lo applichi ad una funzione definita su un intervallo (non lo applichi a dei punti, se ho capito bene il senso della tua domanda).
O forse il problema è solo che non capisci se lo $xi$ di cui il teorema predica l'esistenza può trovarsi o meno in uno degli estremi dell'intervallo...
allora... per la dimostrazione del teorema, è essenziale che il punto $xi$ sia interno all'intervallo $(a,b)$, poichè se esso coincidesse con uno dei suoi estremi ci permetterebbe di considerare incrementi o solo positivi o solo negativi (questo è quanto ho appreso nello studio di questo teorema), ora la mia domanda è: si può considerare che $xi$ estremo di quest'intervallo e dimostrare comunque il teorema?
oppure è una mia interpretazione sbagliata di quanto scritto sul libro?...
Ti dirò la verità, non ho mai studiato la dimostrazione di Lagrange che credo tu abbia in mente.
Ad ogni modo l'ipotesi che $f$ sia derivabile nell'aperto $]a,b[$, e solo continua agli estremi, taglia la testa al toro. Negli estremi la funzione non è richiesto che sia derivabile, mentre in $xi$ deve esserlo, visto che nel punto $xi$ si ha che $f'(xi) = (f(b) - f(a))/(b-a)$. Quindi, se valgono le ipotesi, esiste almeno un punto $xi in ]a,b[$ con questa proprietà il quale è interno all'intervallo. Magari ci sono venticinque punti che fanno questo servizio, ma poco importa. Il teorema di Lagrange ti dice che ce n'è uno e che è interno all'intervallo.
Se hai ancora dubbi potresti postare ciò che effettivamente scrive l'autore del tuo testo...
Ad ogni modo l'ipotesi che $f$ sia derivabile nell'aperto $]a,b[$, e solo continua agli estremi, taglia la testa al toro. Negli estremi la funzione non è richiesto che sia derivabile, mentre in $xi$ deve esserlo, visto che nel punto $xi$ si ha che $f'(xi) = (f(b) - f(a))/(b-a)$. Quindi, se valgono le ipotesi, esiste almeno un punto $xi in ]a,b[$ con questa proprietà il quale è interno all'intervallo. Magari ci sono venticinque punti che fanno questo servizio, ma poco importa. Il teorema di Lagrange ti dice che ce n'è uno e che è interno all'intervallo.
Se hai ancora dubbi potresti postare ciò che effettivamente scrive l'autore del tuo testo...
Aspetta, ora mi è chiaro. Negli estremi dell'intervallo in cui è definita la $f$ non puoi considerare incrementi positivi e negativi (non puoi fare il limite del rapporto incrementale sia da destra che da sinistra), ed è per questo che la $f$, definita su un intervallo, non può dirsi derivabile negli estremi dello stesso.
"Seneca":
Aspetta, ora mi è chiaro. Negli estremi dell'intervallo in cui è definita la $f$ non puoi considerare incrementi positivi e negativi (non puoi fare il limite del rapporto incrementale sia da destra che da sinistra), ed è per questo che la $f$, definita su un intervallo, non può dirsi derivabile negli estremi dello stesso.
ok quindi ciò conferma che ho preso un abbaglio
... grazie mille ...
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo