Integrale logaritmico con i residui
Buongiorno a tutti, vi leggo da tempo ma fino ad ora non avevo mai scritto sul forum.
Ho un problema serio con questi tipi di integrali che non mi permettono di superare l'esame, vivo lontano dall'uni e quindi andare dal prof per me sarebbe un problema in questo momento. Spero possiate aiutarmi, ve ne sarei davvero grato.
Nelle prove di esame mi ritrovo sempre con questi tipi di integrale però senza nessun accenno alla sua risoluzione nemmeno nelle dispense o libri di testo.
Ecco l'integrale
$int_-oo^oo ((log((x)^2)) / ((x^(4))+1))dx$
Sono davvero disperato...cercasi geni in matematicaaaaaa...grazie a tutti quelli che proveranno ad aiutarmi.
Ho un problema serio con questi tipi di integrali che non mi permettono di superare l'esame, vivo lontano dall'uni e quindi andare dal prof per me sarebbe un problema in questo momento. Spero possiate aiutarmi, ve ne sarei davvero grato.
Nelle prove di esame mi ritrovo sempre con questi tipi di integrale però senza nessun accenno alla sua risoluzione nemmeno nelle dispense o libri di testo.
Ecco l'integrale
$int_-oo^oo ((log((x)^2)) / ((x^(4))+1))dx$
Sono davvero disperato...cercasi geni in matematicaaaaaa...grazie a tutti quelli che proveranno ad aiutarmi.
Risposte
Ciao. E' molto tardi e sono stanchissimo, quindi non mi metto a fare i calcoli... Quello che ti posso dire però è che di solito gli integrali con i residui che contengono i logaritmi sono più delicati per il fatto che il logaritmo di un numero complesso è una funzione a più valori. Cmq fissata una determinazione hai dei problemi solo se il polo è sul cammino di integrazione, se non mi sbaglio. Nel tuo caso i poli non stanno sull'asse reale quindi se usi il teorema dei residui non dovresti avere dei grossi problemi.
Spero ti sia d'aiuto e cmq se vuoi domani posso essere un po' più preciso....
Spero ti sia d'aiuto e cmq se vuoi domani posso essere un po' più preciso....
purtroppo non lo riesco ancora a risolvere...applicando il residuo nei punti e^jpi/4 e e^j3pi/4 non mi trovo con il risultato...cmq grazie della risposta.
SIgh
SIgh
Allora....ho fatto i conti come avevamo detto, cioè sommando i residui nei punti $e^(j \pi/4)$ e $e^(j 3/4 \pi)$. Il problema è che il risultato è un numero complesso. E questo non è possibile perchè deve venire un numero reale, siccome integrale di una funzione reale. Supponendo di aver sbagliato i calcoli e ripensando un attimo tutto quanto mi sono accorto che ho trascurato una cosa importantissima. Il logaritmo ha una discontinuità in zero. E zero è sul cammino di integrazione. Quindi secondo me sono proprio fuori strada.
......
Io farei così. Visto che la funzione è pari. Possiamo integrare da zero all'infinito e poi raddoppiare il risultato. Modifichiamo di conseguenza il cammino di integrazione così. Intendo l'ultimo a destra.
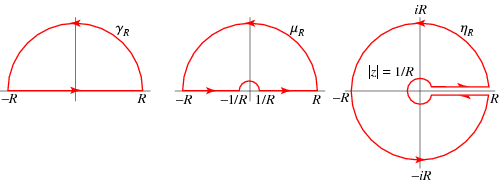
Così prendiamo come poli i quattro zeri del denominatore e evitiamo la singolarità essenziale del logaritmo. Adesso comincia la parte di cui non sono tanto sicuro. Secondo me possiamo scivere una relazione del tipo
$\int_\gamma f(z) dz = 2\pi j sum Res$
dove
$int_\gamma = int_(L^+) + int_(C_R) + int_(L^-) + int_(C_\epsilon)$
Con $C_r$ le due circonferenze e $L^(+-)$ i cammini orizzontali.
Valgono i lemmi del grande e piccolo cerchio, quindi possiamo prendere i limiti, quello che succede è che
$lim_(R->\infty) int_(C_R) f(z) dz = 0$
e
$lim_(\epsilon->0) int_(C_\epsilon) f(z) dz = \pi j Res[f, z=0]$
e poi bisogna tener conto della determinazione scelta per il log. Quindi in $L^+$ usiamo $z = x exp[i0^+]$ e in $L^-$ usiamo $z= x exp[ i (2\pi)^-]$.
Però se sostituisco nella prima relazione tutto questo ottengo un assurdo perchè i due integrali su $L^(+-)$ si elidono a vicenda.......cavolo.......scusa me ne sono accorto solo ora che l'ho scritto, pensavo funzionasse....
Vabbè...continuo a pensarci e poi ti so dire...
......
Io farei così. Visto che la funzione è pari. Possiamo integrare da zero all'infinito e poi raddoppiare il risultato. Modifichiamo di conseguenza il cammino di integrazione così. Intendo l'ultimo a destra.

Così prendiamo come poli i quattro zeri del denominatore e evitiamo la singolarità essenziale del logaritmo. Adesso comincia la parte di cui non sono tanto sicuro. Secondo me possiamo scivere una relazione del tipo
$\int_\gamma f(z) dz = 2\pi j sum Res$
dove
$int_\gamma = int_(L^+) + int_(C_R) + int_(L^-) + int_(C_\epsilon)$
Con $C_r$ le due circonferenze e $L^(+-)$ i cammini orizzontali.
Valgono i lemmi del grande e piccolo cerchio, quindi possiamo prendere i limiti, quello che succede è che
$lim_(R->\infty) int_(C_R) f(z) dz = 0$
e
$lim_(\epsilon->0) int_(C_\epsilon) f(z) dz = \pi j Res[f, z=0]$
e poi bisogna tener conto della determinazione scelta per il log. Quindi in $L^+$ usiamo $z = x exp[i0^+]$ e in $L^-$ usiamo $z= x exp[ i (2\pi)^-]$.
Però se sostituisco nella prima relazione tutto questo ottengo un assurdo perchè i due integrali su $L^(+-)$ si elidono a vicenda.......cavolo.......scusa me ne sono accorto solo ora che l'ho scritto, pensavo funzionasse....
Vabbè...continuo a pensarci e poi ti so dire...
Non vorrei dire una assurdità, ma credo che tu abbia dimenticato 2 residui: praticamente quelli nei punti $e^{j 5/4 \pi}$ e $e^{j 7/4 \pi}$ (che sono le altre due radici quarte di $-1$. E poi c'è un'altra cosa: il dominio io lo disegnerei al contrario: cioè la parte da escludere dovrebbe essere la semiretta negativa $x<0$ e non quella positiva. Un'ultima cosa: quale determinazione hai scelto per il logaritmo?
Edit: mi sono reso conto di una cosa. Il cammino giusto non è il terzo ma il secondo (quello che prende la semicorona nel semipiano superiore.) Ovviamente a quel punto hai bisogno solo di due residui per fare i calcoli. Il fatto che ti venga qualcosa di strano, credo dipenda dal fatto di scegliere la corretta determinazione del logaritmo e vedere che, sul semiasse negativo delle $x$ deve venirti una determinazione pari a $\log x+i\pi$ (con $x>0$.)
Prova così... intanto se ho tempo mi ci metto pure io a fare i conti!
Edit: mi sono reso conto di una cosa. Il cammino giusto non è il terzo ma il secondo (quello che prende la semicorona nel semipiano superiore.) Ovviamente a quel punto hai bisogno solo di due residui per fare i calcoli. Il fatto che ti venga qualcosa di strano, credo dipenda dal fatto di scegliere la corretta determinazione del logaritmo e vedere che, sul semiasse negativo delle $x$ deve venirti una determinazione pari a $\log x+i\pi$ (con $x>0$.)
Prova così... intanto se ho tempo mi ci metto pure io a fare i conti!
Avevo scelto il terzo cammino perchè la funzione da integrare è pari. Il problema secondo me rimane il fatto che la funzione non è integrabile in zero, siccome si comporta come $2*ln x$ che non è integrabile. Occorre considerare lo zero come un polo sul cammino di integrazione e non mi ricordo tanto bene come si fa perchè se non sbaglio bisogna considerare le parti principali e non mi ricordo tanto bene quella parte.......
Ci provo anch'io. 
Prendiamo come determinazione di $\ln(z^2)$ la funzione $\ln(|z^2|)+i"Arg(z^2)=2\ln(|z|)+2i"Arg(z)"$ che e' ben definita su ${"Im"(z)>0}$ e si puo' prolungare con continuita'
a $RR\setminus{0}$ ponendola $\ln(x^2)$ per $x>0$ e $ln(x^2)+2i\pi$ per $x<0$.
Usiamo il cammino 2 (grazie per il disegno ....). E' abbastanza facile vedere che mandando il raggio grande all'infinito il contributo della semicirconferenza grande tende a zero (dato il polinomio di quarto grado al denominatore)
e che pure la semicirconferenza piccola sparisce perche' $\rho\ln(\rho)\to0$ se $\rho\to0$ (il $rho$ a moltiplicare viene dalla misura della semicirconferenza piccola).
Applicando il teorema dei residui otteniamo (dopo che $R\to\infty$ ) NOTA: il logaritmo E' integrabile vicino a zero!!
$\int_{-\infty}^0\frac{\ln(x^2)+2i\pi}{1+x^4}dx+\int_0^{+\infty}\frac{\ln(x^2)}{1+x^4}dx=2\pi i("Res"(e^{i\pi/4})+"Res"(e^{3 i\pi/4}))$
da cui (con un po' di pazienza) si dovrebbe ricavare il risultato cercato.
Mi pare ....
Prendiamo come determinazione di $\ln(z^2)$ la funzione $\ln(|z^2|)+i"Arg(z^2)=2\ln(|z|)+2i"Arg(z)"$ che e' ben definita su ${"Im"(z)>0}$ e si puo' prolungare con continuita'
a $RR\setminus{0}$ ponendola $\ln(x^2)$ per $x>0$ e $ln(x^2)+2i\pi$ per $x<0$.
Usiamo il cammino 2 (grazie per il disegno ....). E' abbastanza facile vedere che mandando il raggio grande all'infinito il contributo della semicirconferenza grande tende a zero (dato il polinomio di quarto grado al denominatore)
e che pure la semicirconferenza piccola sparisce perche' $\rho\ln(\rho)\to0$ se $\rho\to0$ (il $rho$ a moltiplicare viene dalla misura della semicirconferenza piccola).
Applicando il teorema dei residui otteniamo (dopo che $R\to\infty$ ) NOTA: il logaritmo E' integrabile vicino a zero!!
$\int_{-\infty}^0\frac{\ln(x^2)+2i\pi}{1+x^4}dx+\int_0^{+\infty}\frac{\ln(x^2)}{1+x^4}dx=2\pi i("Res"(e^{i\pi/4})+"Res"(e^{3 i\pi/4}))$
da cui (con un po' di pazienza) si dovrebbe ricavare il risultato cercato.
Mi pare ....
Esatto Vicious, era qui che volevo arrivare! Solo che, sinceramente, avevo poca voglia di fare i conti espliciti! 




 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo