Integrale carino, ma non troppo

[rocco.g1]

mi ero messo a risolvere questo integrale, solo che per come avevo impostato i primi passaggi la cosa risultava abbastanza difficile.
l'integrale è questo :



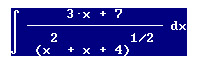
io avevo portato al numeratore la radice elevando tutto il denominatore alla meno un mezzo, in modo da usare la formula tra prodotti...ma così esce troppo complicato... come is potrebbe fare ? credo di dovrebbe togliere la radice, ma non so come, non mi è mai capitato un integrale così...



Modificato da - rocco.g il 11/03/2004 20:10:16

[Principe2]

ti scrivo i passaggi in italiano perchè in matematica ci metto troppo:

1) porti il tre fuori; il numeratore ti viene x+7/3

2) moltiplichi per due dentro l'integrale; numeratore 2x+14/3

3) stacchi il numeratore in due integrali al fine di avere:
numeratore primo integrale: 2x +1; numeratore secondo integrale: 11/3

4) il primo integrale è immediato, il secondo si risolve con una formula che ora non mi sovviene ma che tu dovresti conoscere.

ciao, ubermensch

[Principe2]

la formula che ti dicevo è:

 





        1

----------------dx = ln|x+p/2+ [(x+p/2)^2 + q - p^2/4] |

     (x^2+px+q)

ciao

[rocco.g1]

ciao,
grazie per avermi risposto ! si la formula la conoscevo , solo che non sapevo si potesse fare lo stesso procedimento con il log anke se c'è una radice... quindi lo posso fare sempre ? o questo era solo un caso ? cioè se al denominatore mi trovo un polinomio di grado n sotto radice, posso sempre ricondurlo ad un log facendo in modo ovviamente di avere la sua derivata al numeratore ?

[Principe2]

credo che dipenda da quello che hai al numeratore; infatti, dopo aver diviso in due integrali, allora, al numeratore del secondo, ti deve rimanere un polinomio di grado n/2-1. se n=2 infatti si ha il caso particolare che hai solo un termine noto che puoi considerare come monomio di grado 2/2-1=0.

comunque, solitamente, questi integrali si usano poco. io sono certo di non aver mai usato quelle formule, infatti me le sono dovute andare a cercare su un libro!!

ciao, ubermensch

[rocco.g1]

eh lo so che si usano poco, purtroppo il mio professore mette sempre e solo esercizi che hanno casi particolari...se ti dico il limite che faceva parte dello stesso set di esercizi dell'appello in cui c'era anke questo integrale capisci cosa voglio dire

[Principe2]

mettilo sto limite!.. un pò di esercizio non fa mai male...

[rocco.g1]

ok, lo metto in un altro post però, per non andare OT qui...