Insieme Contraibile
Ciao a tutti, ho un nuovo problema che da sola non riesco ad affrontare.
Devo stabilire se il seguente insieme è contraibile (semplicemente connesso):
$\{(x+y,xy) in RR^2:x^2+y^2 <=1 \} $
Senza pensarci troppo avevo posto $\alpha=x+y$ e $\beta=xy$ e quindi l'insieme diventava:
$\{(\alpha,\beta) in RR^2:\alpha^2 - 2\beta <=1 \}$
che equivale a $\beta >= (\alpha^2-1)/2$
Vedendolo in questo modo direi che l'insieme è semplicemente connesso ed infatti l'insieme lo è.
Ma non sono sicura che la sostituzione che ho fatto possa andar bene a causa di quel $\beta = xy$ e da qui nasce la mia crisi sull'intero esercizio xD
Suggerimenti?
Devo stabilire se il seguente insieme è contraibile (semplicemente connesso):
$\{(x+y,xy) in RR^2:x^2+y^2 <=1 \} $
Senza pensarci troppo avevo posto $\alpha=x+y$ e $\beta=xy$ e quindi l'insieme diventava:
$\{(\alpha,\beta) in RR^2:\alpha^2 - 2\beta <=1 \}$
che equivale a $\beta >= (\alpha^2-1)/2$
Vedendolo in questo modo direi che l'insieme è semplicemente connesso ed infatti l'insieme lo è.
Ma non sono sicura che la sostituzione che ho fatto possa andar bene a causa di quel $\beta = xy$ e da qui nasce la mia crisi sull'intero esercizio xD
Suggerimenti?
Risposte
E' interessante, in effetti non è ovvio che i cambi di variabile preservino la connessione semplice. Se la funzione \(f(x, y)=(x+y, xy)\) è continua e ingettiva questo è vero:
https://math.stackexchange.com/question ... ted-domain
ma non sono proprio sicuro sicuro che quella funzione sia ingettiva, che poi è lo stessissimo dubbio tuo
https://math.stackexchange.com/question ... ted-domain
ma non sono proprio sicuro sicuro che quella funzione sia ingettiva, che poi è lo stessissimo dubbio tuo
Certo che il cambiamento di variabili non è iniettivo... Entrambe le coordinate sono funzioni simmetriche delle variabili, le quali variano in un insieme molto simmetrico.
Quindi come dovrei procedere per stabilire senza intoppi che l'insieme è semplicemente connesso? (ovviamente questo lo so perché la soluzione dice che lo è senza però aggiungere altro).
Ho provato a guardare il problema in coordinate polari, ovvero:
$(\rho cos\theta + \rho sin\theta , \rho^2 sin\theta cos\theta )$ con $-1<= \rho <= 1$
ma non vedo nulla di più rispetto a prima
Ho provato a guardare il problema in coordinate polari, ovvero:
$(\rho cos\theta + \rho sin\theta , \rho^2 sin\theta cos\theta )$ con $-1<= \rho <= 1$
ma non vedo nulla di più rispetto a prima
"Sbrain":
Ho provato a guardare il problema in coordinate polari
Brava, ci ho pensato pure io.

Ma non ho concluso molto.

"gugo":Ho capito, e naturalmente hai ragione, per esempio \(f(x, y)=f(y, x)\). Ma non è che la restrizione di \(f\) al semicerchio \(x^2+y^2\le 1, y\ge x\) è iniettiva? Se così fosse saremmo a cavallo: l'insieme dato è l'immagine attraverso \(f\) del semicerchio che è un insieme semplicemente connesso.
Certo che il cambiamento di variabili non è iniettivo... Entrambe le coordinate sono funzioni simmetriche delle variabili, le quali variano in un insieme molto simmetrico.
"dissonance":
[quote="Sbrain"]
Ho provato a guardare il problema in coordinate polari
Brava, ci ho pensato pure io.

Ma non ho concluso molto.

"gugo":Ho capito, e naturalmente hai ragione, per esempio \(f(x, y)=f(y, x)\). Ma non è che la restrizione di \(f\) al semicerchio \(x^2+y^2\le 1, y\ge x\) è iniettiva? Se così fosse saremmo a cavallo: l'insieme dato è l'immagine attraverso \(f\) del semicerchio che è un insieme semplicemente connesso.[/quote]
Certo che il cambiamento di variabili non è iniettivo... Entrambe le coordinate sono funzioni simmetriche delle variabili, le quali variano in un insieme molto simmetrico.
Ma perché stai considerando solo la parte con $y>=x$? Comunque non saprei rispondere, era giusto per capire che strada stessi provando a percorrere.
perché stai considerando solo \(y\ge x\)
Perché se chiami \(D=\{x^2+y^2\le 1\}\), e \(D_+=D\cap \{y\ge x\}, D_-=D\cap\{x \le y\}\) allora \(f(D)=f(D_+)=f(D_-)\). Questo consegue dalla simmetria \(f(x, y)=f(y,x)\).
Hai per caso trovato la soluzione? Sono curioso
Ho fatto un plot spartano dell'insieme:

(da immaginarsi come colorato uniformemente - no aree bianche nella parte bassa).
La parte alta della frontiera è un pezzo della parabola \(Y=X^2/4\), la parte bassa è un pezzo della parabola \(Y=\frac12X^2 -\frac12\). La parabola alta è l'immagine attraverso la mappa \((X, Y)=(x+y, xy)\) del segmento ottenuto intersecando la retta \(y=x\) con il disco unitario \(x^2+y^2\le 1\). La parabola bassa è l'immagine attraverso la stessa mappa del bordo del disco unitario \(x^2+y^2=1\).

(da immaginarsi come colorato uniformemente - no aree bianche nella parte bassa).
La parte alta della frontiera è un pezzo della parabola \(Y=X^2/4\), la parte bassa è un pezzo della parabola \(Y=\frac12X^2 -\frac12\). La parabola alta è l'immagine attraverso la mappa \((X, Y)=(x+y, xy)\) del segmento ottenuto intersecando la retta \(y=x\) con il disco unitario \(x^2+y^2\le 1\). La parabola bassa è l'immagine attraverso la stessa mappa del bordo del disco unitario \(x^2+y^2=1\).
Semplicemente connesso e contraibile non sono sinonimi. Tutte le sfere \(S^{\ge 2}\) sono semplicemente connesse, nessuna è contraibile.
@killing_buddha: qui si parla di aperti di \(\mathbb R^2\), nel qual caso le due nozioni coincidono:
http://math.ucr.edu/~res/math205B/ahlfors.pdf
Tu come dimostreresti che quell'insieme è semplicemente connesso? Ci ho pensato nei ritagli di tempo ma devo ammettere che mi ha messo un pochino in difficoltà.
http://math.ucr.edu/~res/math205B/ahlfors.pdf
Tu come dimostreresti che quell'insieme è semplicemente connesso? Ci ho pensato nei ritagli di tempo ma devo ammettere che mi ha messo un pochino in difficoltà.
Scusate, ma non abbiamo finito?
Insomma, una volta stabilito che $f(D)=f(D^+)$ e che $f$ è continua ed iniettiva su $D^+$, non siamo a cavallo?
Insomma, una volta stabilito che $f(D)=f(D^+)$ e che $f$ è continua ed iniettiva su $D^+$, non siamo a cavallo?
Certamente ma manca la dimostrazione che \(f\) sia iniettiva su \(D^+\).
Vabbè, ma basta vedere se il sistema:
\[
\begin{cases}
x+y = \alpha\\
xy = \beta
\end{cases}
\]
ha unica soluzione con $y>=x$, il che non mi pare proprio proibitivo... O no?
\[
\begin{cases}
x+y = \alpha\\
xy = \beta
\end{cases}
\]
ha unica soluzione con $y>=x$, il che non mi pare proprio proibitivo... O no?
L'immagine mediante $f$ delle circonferenze \(\gamma_a : t\mapsto (a\cos t, a\sin t)\), che al variare di \(a\in[0,1]\) foliano il disco unitario, è una famiglia di segmenti di parabola che coprono $T= f(D^2)$:
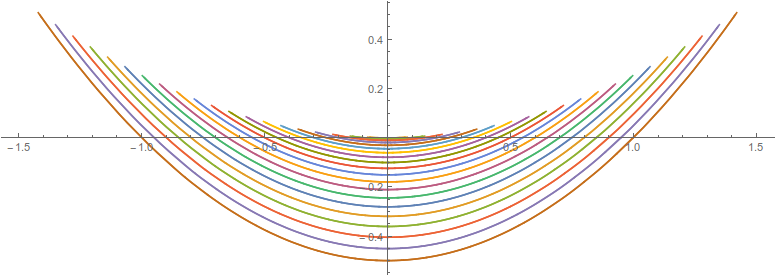
L'insieme $T$ ora è stellato, al vertice della parabola \(\gamma_1\). Gli insiemi stellati sono contraibili al punto di stella, con l'omotopia affine che contrae sul punto di stella.

L'insieme $T$ ora è stellato, al vertice della parabola \(\gamma_1\). Gli insiemi stellati sono contraibili al punto di stella, con l'omotopia affine che contrae sul punto di stella.
Mi sembra corretto, bella soluzione e bel disegno. 
---
Una cosa che mi ha spiazzato, in questo esercizio, è una strana configurazione delle simmetrie. La figura \(f(D^2)\) (adotto qui la notazione \(D^2\) di KB per il disco unitario) è simmetrica rispetto alla riflessione \((x, y) \mapsto (-x, y)\), ma NON è simmetrica rispetto a \((x, y)\mapsto (x, -y)\). E questo mi sembrava strano, perché sia \(D^2=\{x^2+y^2\le1\}\) sia \(f(x, y)=(x+y, xy)\) sono invarianti per permutazioni di coordinate: per quale motivo la riflessione della \(x\) è una simmetria mentre la riflessione della \(y\) non lo è?
Curioso.

---
Una cosa che mi ha spiazzato, in questo esercizio, è una strana configurazione delle simmetrie. La figura \(f(D^2)\) (adotto qui la notazione \(D^2\) di KB per il disco unitario) è simmetrica rispetto alla riflessione \((x, y) \mapsto (-x, y)\), ma NON è simmetrica rispetto a \((x, y)\mapsto (x, -y)\). E questo mi sembrava strano, perché sia \(D^2=\{x^2+y^2\le1\}\) sia \(f(x, y)=(x+y, xy)\) sono invarianti per permutazioni di coordinate: per quale motivo la riflessione della \(x\) è una simmetria mentre la riflessione della \(y\) non lo è?
Curioso.
A parte l’intuizione geometrica dietro il disegnino di k_b, provo ad argomentare con qualche noiosissimo contrariello.
Il sistema scritto sopra ha effettivamente unica soluzione nel semipiano che sovrasta la bisettrice del primo e terzo quadrante, in particolare la soluzione è:
\[ \begin{cases} x = \frac{\alpha - \sqrt{\alpha^2 - 4 \beta}}{2} \\ y = \frac{\alpha + \sqrt{\alpha^2 - 4 \beta}}{2} \end{cases} \]
sotto l’ovvia condizione $alpha^2 - 4beta >= 0$.
In particolare, da ciò segue che la funzione $f$ mappa il semipiano $\Pi$ individuato dalla limitazione $y >= x$ nella regione $R$ individuata da $beta <= 1/4 alpha^2$.
Da quanto trovato si può pure vedere che: i semiassi $alpha$ positivo e negativo sono i trasformati, rispettivamente, dei semiassi $y$ positivo ed $x$ negativo; le semirette verticali parallele all’asse $beta$ di equazione \(\alpha = \text{costante}\) sono trasformate di semirette parallele alla bisettrice di equazione $y=-x$; le rette parallele all’asse $alpha$ di equazione \(\beta = \text{costante}\) sono trasformate di rami di iperboli equilatere con asintoti lungo gli assi coordinati $x$ ed $y$.
Ne viene che $f$ ristretta alla porzione di disco unitario chiuso contenuto nel semipiano $Pi$ è biiettive e continua, perciò preserva la semplice connessione.
@dissonance: non mi sorprende che la simmetria che dici sia l’unica che funziona... Anche se stai confondendo piano di partenza e di arrivo della $f$.
Infatti, hai $f(-x,-y) = (- (x+y), x y)$ il che significa che assoggettando il piano d’arrivo $Oalpha beta$ alla simmetria rispetto all’asse $beta$, i.e. scambiando $alpha$ con $-alpha$, si ottiene un punto che è il trasformato del simmetrico di $(x, y)$ rispetto all’origine di $Oxy$.
D’altra parte, assoggettando il piano $Oalpha beta$ alla simmetria rispetto all’asse $alpha$, ossia cambiando $beta$ col suo opposto $-beta$, non succede nulla di buono perché dovresti cambiare i segni ad uno solo tra $x$ ed $y$, il che ti cambia irrimediabilmente il valore di $x+y$.
"gugo82":
Vabbè, ma basta vedere se il sistema:
\[ \begin{cases} x+y = \alpha\\ xy = \beta \end{cases} \]
ha unica soluzione con $ y>=x $, il che non mi pare proprio proibitivo... O no?
Il sistema scritto sopra ha effettivamente unica soluzione nel semipiano che sovrasta la bisettrice del primo e terzo quadrante, in particolare la soluzione è:
\[ \begin{cases} x = \frac{\alpha - \sqrt{\alpha^2 - 4 \beta}}{2} \\ y = \frac{\alpha + \sqrt{\alpha^2 - 4 \beta}}{2} \end{cases} \]
sotto l’ovvia condizione $alpha^2 - 4beta >= 0$.
In particolare, da ciò segue che la funzione $f$ mappa il semipiano $\Pi$ individuato dalla limitazione $y >= x$ nella regione $R$ individuata da $beta <= 1/4 alpha^2$.
Da quanto trovato si può pure vedere che: i semiassi $alpha$ positivo e negativo sono i trasformati, rispettivamente, dei semiassi $y$ positivo ed $x$ negativo; le semirette verticali parallele all’asse $beta$ di equazione \(\alpha = \text{costante}\) sono trasformate di semirette parallele alla bisettrice di equazione $y=-x$; le rette parallele all’asse $alpha$ di equazione \(\beta = \text{costante}\) sono trasformate di rami di iperboli equilatere con asintoti lungo gli assi coordinati $x$ ed $y$.
Ne viene che $f$ ristretta alla porzione di disco unitario chiuso contenuto nel semipiano $Pi$ è biiettive e continua, perciò preserva la semplice connessione.
@dissonance: non mi sorprende che la simmetria che dici sia l’unica che funziona... Anche se stai confondendo piano di partenza e di arrivo della $f$.
Infatti, hai $f(-x,-y) = (- (x+y), x y)$ il che significa che assoggettando il piano d’arrivo $Oalpha beta$ alla simmetria rispetto all’asse $beta$, i.e. scambiando $alpha$ con $-alpha$, si ottiene un punto che è il trasformato del simmetrico di $(x, y)$ rispetto all’origine di $Oxy$.
D’altra parte, assoggettando il piano $Oalpha beta$ alla simmetria rispetto all’asse $alpha$, ossia cambiando $beta$ col suo opposto $-beta$, non succede nulla di buono perché dovresti cambiare i segni ad uno solo tra $x$ ed $y$, il che ti cambia irrimediabilmente il valore di $x+y$.
Grazie Gugo! Proprio bella questa soluzione. 

@dissonance: Sese... Un colpo al cerchio ed uno alla botte. Da te non me l’aspettavo! 


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo