Esercizio: Area di una superficie
Spero nn vi dispiaccia se in questo periodo posterò molte domande sul forum..
Comunque sto' cercando di risolvere un esercizio d'esame sul calcolo dell'area di una superficie, volevo capire se ho ragionato in modo corretto:
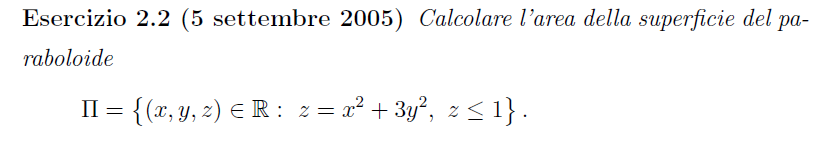
[edit... tt quello che avevo postato era sbagliato...]
Devo riuscire a parametrizzare la curva giusto? da dove parto? (intanto riprovo a risolvere e edito se trovo la soluzione:
Mah.. vi dico come ho fatto... boh.. T__T
pongo $ x = mu*cos alpha $, $ y = mu*sen alpha $, quindi $ z = mu^2 *cos^2 alpha +3*mu^2*sen^2 alpha $
modifico 1 po' z: $ z = mu^2*(cos^2 alpha +3*sen^2 alpha) => z= mu^2(cos^2 alpha +3(1-cos^2 alpha) => z = mu^2(3-2*cos^2 alpha)$
mi ci sn avvicinato?
Poi, considerando che $z leq 1$, notando che il valore massimo che può assumere $ (3-2cos^2 alpha)$ è $3$, ho posto:
$mu^2 *3 leq 1$, quindi $mu in [0,1/sqrt 3]$
ho scritto qualcosa di corretto?
Comunque sto' cercando di risolvere un esercizio d'esame sul calcolo dell'area di una superficie, volevo capire se ho ragionato in modo corretto:
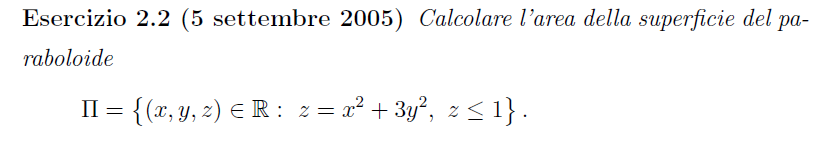
[edit... tt quello che avevo postato era sbagliato...]
Devo riuscire a parametrizzare la curva giusto? da dove parto? (intanto riprovo a risolvere e edito se trovo la soluzione:
Mah.. vi dico come ho fatto... boh.. T__T
pongo $ x = mu*cos alpha $, $ y = mu*sen alpha $, quindi $ z = mu^2 *cos^2 alpha +3*mu^2*sen^2 alpha $
modifico 1 po' z: $ z = mu^2*(cos^2 alpha +3*sen^2 alpha) => z= mu^2(cos^2 alpha +3(1-cos^2 alpha) => z = mu^2(3-2*cos^2 alpha)$
mi ci sn avvicinato?
Poi, considerando che $z leq 1$, notando che il valore massimo che può assumere $ (3-2cos^2 alpha)$ è $3$, ho posto:
$mu^2 *3 leq 1$, quindi $mu in [0,1/sqrt 3]$
ho scritto qualcosa di corretto?
Risposte
Devi parametrizzare la superficie:
$\{(x=\rhocos\phi),(y=\rho/sqrt(3)sen\phi),(z=\rho^2):}$
con $0<=\rho<=1$ e $0<=\phi<2\pi$.
$\{(x=\rhocos\phi),(y=\rho/sqrt(3)sen\phi),(z=\rho^2):}$
con $0<=\rho<=1$ e $0<=\phi<2\pi$.
Scusa, volendo funziona anche:
$ { ( x=mu cos alpha ),( y=mu sen alpha ),( z = mu^2(3-2cos^2 alpha) ):} $
con $ 0 leq mu leq 1/sqrt 3$ e $0 leq alpha leq 2pi$ ???
Tu come hai ragionato per arrivare alla (migliore) soluzione che mi hai proposto?
$ { ( x=mu cos alpha ),( y=mu sen alpha ),( z = mu^2(3-2cos^2 alpha) ):} $
con $ 0 leq mu leq 1/sqrt 3$ e $0 leq alpha leq 2pi$ ???
Tu come hai ragionato per arrivare alla (migliore) soluzione che mi hai proposto?
Non puoi assolutamente esprimere l'insieme $mu^2(3-2*cos^2 alpha)<=1$ come $0<=\mu<=1/sqrt(3)$ e $0<=\alpha<2\pi$, è evidente che la condizione su $\mu$ debba dipendere da $\alpha$. Nell'altro modo, si tratta di una parametrizzazione standard, l'insieme risultante si esprime molto più facilmente, proprio perchè la condizione su $\rho$ non dipende da $\phi$.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo