Curvatura massima
Ciao! Ho un problema urgente.
Come si calcola la curvatura max/min di una superficie?
Sono grata di ogni risposta!
Come si calcola la curvatura max/min di una superficie?
Sono grata di ogni risposta!
Risposte
ma in analisi o in geometria differenziale?
in analisi prova a fare il determinate della hessiana(non sostituendo i valori ma metterndoci le funzioni generiche) e trovare i massimi e minimi della funzione che esce fuori...
in geometria differenziale non saprei
in analisi prova a fare il determinate della hessiana(non sostituendo i valori ma metterndoci le funzioni generiche) e trovare i massimi e minimi della funzione che esce fuori...
in geometria differenziale non saprei
Grazie mille! Ci proverò...
cara lauragiulia
un discorso abbastanza ben fatto sulla curvatura lo puoi trovare in http://www.vialattea.net/curvatura/. Nel caso in due dimensioni, più semplice, esiste una formula che fornisce l’inverso della curvatura, vale a dire il raggio di curvatura e questa è data da…
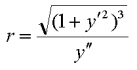[1]
Trattandosi di una funzione in x essa può essere massimizata o minimizzata con le regole usuali dell'analisi. Due semplici esempi...
Esempio 1 [parabola]…
y=x^2 , y’=2*x, y’’=2, r= [(1+4*x^2)^3/2]/2 [2]
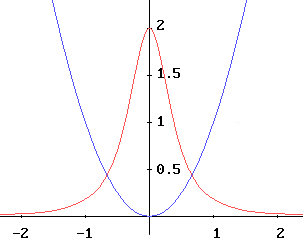
La curvatura è massima, ossia il raggio di curvatura è minimo, per x=0. Esempio 2 [iperbole]…
y=1/x, y’=-1/x^2,y’’=2/x^3, r=[(1+x^4)^3/2]/(2*x^3) [3]
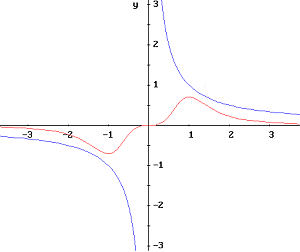
La curvatura è massima, ossia il raggio di curvatura è minimo, per x=-1 e x=1…
Per quanto riguarda la curvatura di superfici, ossia non in due bensì in tre dimensioni, il discorso è un poco più complesso, a meno che non si tratti di superfici di rotazione le quali possono essere trattate come curve...
cordiali saluti
lupo grigio
un discorso abbastanza ben fatto sulla curvatura lo puoi trovare in http://www.vialattea.net/curvatura/. Nel caso in due dimensioni, più semplice, esiste una formula che fornisce l’inverso della curvatura, vale a dire il raggio di curvatura e questa è data da…
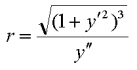[1]Trattandosi di una funzione in x essa può essere massimizata o minimizzata con le regole usuali dell'analisi. Due semplici esempi...
Esempio 1 [parabola]…
y=x^2 , y’=2*x, y’’=2, r= [(1+4*x^2)^3/2]/2 [2]
La curvatura è massima, ossia il raggio di curvatura è minimo, per x=0. Esempio 2 [iperbole]…
y=1/x, y’=-1/x^2,y’’=2/x^3, r=[(1+x^4)^3/2]/(2*x^3) [3]
La curvatura è massima, ossia il raggio di curvatura è minimo, per x=-1 e x=1…
Per quanto riguarda la curvatura di superfici, ossia non in due bensì in tre dimensioni, il discorso è un poco più complesso, a meno che non si tratti di superfici di rotazione le quali possono essere trattate come curve...
cordiali saluti
lupo grigio
Grazie,Lupo grigio, sei stato di grande aiuto!
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo