Condizione di Lipschitz
Sulla base di un altro topic, mi domandavo sotto quali ipotesi una funzione uniformemente continua fosse lipschitziana.
Inoltre vorrei un esempio di funzione uniformemente continua ma non lipschitziana.
Inoltre vorrei un esempio di funzione uniformemente continua ma non lipschitziana.
Risposte
Trovato l'esempio, lo scrivo nel caso qualcuno fosse interessato:
$sqrt(x)$ è uniformemente continua in $[0,+oo[$ ma non è lipschitziana in esso
Rimane in ogni caso aperta la prima questione...
$sqrt(x)$ è uniformemente continua in $[0,+oo[$ ma non è lipschitziana in esso
Rimane in ogni caso aperta la prima questione...
Credo che $C^1$ sul chiuso sia sufficiente per via di Lagrange...
Sottointendevi "chiuso e limitato"?
Il problema proposto da Kroldar mi ha fatto ricordare di un altro problema da me posto alla vostra attenzione la scorsa estate e lasciato poi nel ‘dimeticatoio’…
https://www.matematicamente.it/f/viewtopic.php?t=10691
Il problema in questione era stato da me demoninato ‘problema del cucù’ e si riferiva al movimento ‘su e giù’ della ‘ragazzotta’ che vedete qui…

Il problema di Cauchy in questo caso è il seguente…
$x’= sqrt(1-x^2)$ con $x(0)=-1$ (1)
Ricordo bene che proprio Kroldar ha trovato la soluzione $x=-cos t$, per la quale è facile verificarde che soddisfa la (1)…
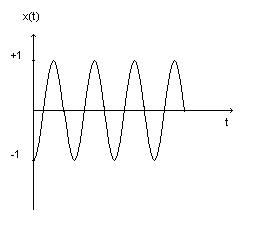
Ok fin qui… il quesito da me posto era tuttavia un altro e cioè se la (1) avesse una e una sola soluzione massimale [chiedo scusa per la ‘parolona’…]. La risposta a questo quesito è negativa in quanto un’altra possibile soluzione è quella qui sotto rappresentata, nella quale i valori $t_0$ può essere qualsiasi purchè $>0$ e $t_1$ anch’esso qualsiasi purchè $>t_0+pi$…

La (1) pertanto ha infinite soluzioni e la domanda a questo punto è assai semplice: perché?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature[/img]
https://www.matematicamente.it/f/viewtopic.php?t=10691
Il problema in questione era stato da me demoninato ‘problema del cucù’ e si riferiva al movimento ‘su e giù’ della ‘ragazzotta’ che vedete qui…

Il problema di Cauchy in questo caso è il seguente…
$x’= sqrt(1-x^2)$ con $x(0)=-1$ (1)
Ricordo bene che proprio Kroldar ha trovato la soluzione $x=-cos t$, per la quale è facile verificarde che soddisfa la (1)…
Ok fin qui… il quesito da me posto era tuttavia un altro e cioè se la (1) avesse una e una sola soluzione massimale [chiedo scusa per la ‘parolona’…]. La risposta a questo quesito è negativa in quanto un’altra possibile soluzione è quella qui sotto rappresentata, nella quale i valori $t_0$ può essere qualsiasi purchè $>0$ e $t_1$ anch’esso qualsiasi purchè $>t_0+pi$…
La (1) pertanto ha infinite soluzioni e la domanda a questo punto è assai semplice: perché?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature[/img]
"Kroldar":
Sottointendevi "chiuso e limitato"?
Si si... altrimenti si ha la lipshitzianità solo sui compatti. In generale direi che $f \in W^{1,\infty}$ va bene. ($f'$ limitata in modulo).
"lupo grigio":
La (1) pertanto ha infinite soluzioni e la domanda a questo punto è assai semplice: perché?
Appunto perché la funzione $\sqrt(1-x^2)$ non è lipshitz...

"Kroldar":
Trovato l'esempio, lo scrivo nel caso qualcuno fosse interessato:
$sqrt(x)$ è uniformemente continua in $[0,+oo[$ ma non è lipschitziana in esso
Rimane in ogni caso aperta la prima questione...
per informazione, questo avviene perchè il modulo di continuità di questa funzione non può essere maggiorato da nessuna retta passante per l'origine (infatti il suo modulo di continuità è $\omega(s)=Cs^(1/2)$ se ben ricordo, con la costante che lascio trovare ai volenterosi (si dice che è una funzione $1/2$-Holderiana)...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo