Carattere serie
Ragazzi, tranne che per le serie di leibniz, con tutte le altre ho sempre problemi [:)]
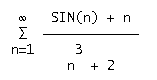
come lo studiereste il suo comportamento ? cioè mi serve solo sapere se converge o meno, non mi serve sapere il risultato della serie...
ho provato alcuni metodi, però non mi è venuto fuori niente di buono...
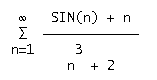
come lo studiereste il suo comportamento ? cioè mi serve solo sapere se converge o meno, non mi serve sapere il risultato della serie...
ho provato alcuni metodi, però non mi è venuto fuori niente di buono...
Risposte
Io farei così.
il sin(x) è una funzione limitata, quindi
la serie data è compresa tra (-1 + n)/((n^3) + 2) e
(1 + n)/((n^3) + 2)
quindi mi studio (1 + n)/((n^3) + 2)
Utilizzo il criterio asintotico utlizzando la serie 1/(n^2) che converge e visto che il limite è 1 il criterio asintotico mi dice che anche la serie al numeratore converge
La serie data è minore di una convergente e quindi per il criterio del confronto converge anch'essa!!
Spero di non aver detto troppe baggianate
il sin(x) è una funzione limitata, quindi
la serie data è compresa tra (-1 + n)/((n^3) + 2) e
(1 + n)/((n^3) + 2)
quindi mi studio (1 + n)/((n^3) + 2)
Utilizzo il criterio asintotico utlizzando la serie 1/(n^2) che converge e visto che il limite è 1 il criterio asintotico mi dice che anche la serie al numeratore converge
La serie data è minore di una convergente e quindi per il criterio del confronto converge anch'essa!!
Spero di non aver detto troppe baggianate
ciao,
noi però il criterio asintotico non l'abbiamo fatto, di che si tratta ? o se c'è un altro modo senza usarlo...
noi però il criterio asintotico non l'abbiamo fatto, di che si tratta ? o se c'è un altro modo senza usarlo...
Siano a, b due successioni positive
Se esiste lim n-->+inf a/b = l con 0
Se esiste lim n-->+inf a/b = l con 0
ah capito, grazie 

Forse si puo' evitare il criterio asintotico
osservando che:
(1+n)/(n^3+2)<(1+n)/n^3=1/n^3+1/n^2
e che le due successioni {1/n^3}ed {1/n^2}
sono entrambe convergenti perche' successioni
armoniche generalizzate con esponente >1.
karl.
osservando che:
(1+n)/(n^3+2)<(1+n)/n^3=1/n^3+1/n^2
e che le due successioni {1/n^3}ed {1/n^2}
sono entrambe convergenti perche' successioni
armoniche generalizzate con esponente >1.
karl.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo