Alle Prese Con Gli Esercizi Di Analisi II
Salve a tutti creo un nuovo thread nel quale discutere di esercizi di Analisi II, seguendo il consiglio datomi in precedenza posterò traccia e tentativo di soluzione
esercizio 1
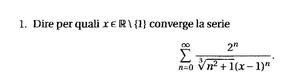
tentativo di soluzione:


spero di aver postato correttamente
esercizio 1
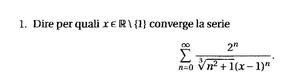
tentativo di soluzione:


spero di aver postato correttamente

Risposte
Mi sono reso conto che nella verifica per x=3 ho usato il criterio del confronto erroneamente 
il criterio dice:
Date due serie Ak e Bk a termini non negativi e se ak < bk allora
se Ak diverge allora Bk diverge
se Bk converge allora Ak converge
nel mio caso Bk diverge quindi non la posso confrontare, tuttavia ho utilizzato il criterio degli infinitesimi:

il criterio dice:
Date due serie Ak e Bk a termini non negativi e se ak < bk allora
se Ak diverge allora Bk diverge
se Bk converge allora Ak converge
nel mio caso Bk diverge quindi non la posso confrontare, tuttavia ho utilizzato il criterio degli infinitesimi:

@ androidiano: Per favore, evita di postare immagini.
Purtroppo, i siti di hosting cancellano periodicamente le immagini caricate, sicché qui sul forum ci ritroviamo thread acefali in capo a due mesi o poco più.
L'unico modo di conservare thread leggibili è trascrivere i testi e gli svolgimenti usando il TeX; perciò, ti chiedo di sforzarti ad usarlo.
Inoltre, un titolo più specifico non guasterebbe.
Purtroppo, i siti di hosting cancellano periodicamente le immagini caricate, sicché qui sul forum ci ritroviamo thread acefali in capo a due mesi o poco più.
L'unico modo di conservare thread leggibili è trascrivere i testi e gli svolgimenti usando il TeX; perciò, ti chiedo di sforzarti ad usarlo.
Inoltre, un titolo più specifico non guasterebbe.
Salve ho corretto il titolo, ho caricato immagini perché ho paura di usare il teX mi sembra complicato e poco veloce, per imparare a usare il tex devo leggere qui? http://www.matematicamente.it/forum/viewtopic.php?f=18&t=26179
Cortesemente può dirmi se gli esercizi che ho postato sono corretti, sono disperato per la prova che dovrò sostenere tra qualche giorno
Cortesemente può dirmi se gli esercizi che ho postato sono corretti, sono disperato per la prova che dovrò sostenere tra qualche giorno
Esercizio 3
Trovare il centro, il raggio di convergenza e l'insieme di convergenza della serie
$\sum_{n=0}^∞ sqrt(n)(2x-5)^(2n)$
è una serie di potenze di centro = $5/2 $ e $a_n$ = $sqrt(n)$
trovo il raggio di convergenza
$lim_(n->∞)sqrt(n+1)/sqrt(n)$ = 1 -> raggio di convergenza = 1
La serie converge per ogni x: $|x - 5/2|<1$
quindi l'insieme di convergenza E $sup$ $(3/2, 7/2)$
adesso verifico cosa succede negli estremi:
x = $3/2$
$\sum_{n=0}^∞ sqrt(n)(3-5)^(2n)$ = $\sum_{n=0}^∞ sqrt(n)(-2)^(2n)$ = $\sum_{n=0}^∞ sqrt(n)4^(n)$
che è una serie a termini positivi che non verifica la condizione necessaria per la convergenza -> diverge
x = $7/2$
$\sum_{n=0}^∞ sqrt(n)(7-5)^(2n)$ = $\sum_{n=0}^∞ sqrt(n)4^(n)$ diverge
quindi insieme di convergenza = $(3/2, 7/2)$
@ gugo82 sono stato bravo?
Trovare il centro, il raggio di convergenza e l'insieme di convergenza della serie
$\sum_{n=0}^∞ sqrt(n)(2x-5)^(2n)$
è una serie di potenze di centro = $5/2 $ e $a_n$ = $sqrt(n)$
trovo il raggio di convergenza
$lim_(n->∞)sqrt(n+1)/sqrt(n)$ = 1 -> raggio di convergenza = 1
La serie converge per ogni x: $|x - 5/2|<1$
quindi l'insieme di convergenza E $sup$ $(3/2, 7/2)$
adesso verifico cosa succede negli estremi:
x = $3/2$
$\sum_{n=0}^∞ sqrt(n)(3-5)^(2n)$ = $\sum_{n=0}^∞ sqrt(n)(-2)^(2n)$ = $\sum_{n=0}^∞ sqrt(n)4^(n)$
che è una serie a termini positivi che non verifica la condizione necessaria per la convergenza -> diverge
x = $7/2$
$\sum_{n=0}^∞ sqrt(n)(7-5)^(2n)$ = $\sum_{n=0}^∞ sqrt(n)4^(n)$ diverge
quindi insieme di convergenza = $(3/2, 7/2)$
@ gugo82 sono stato bravo?
accidenti penso di aver sbagliato l'esercizio 3  lo rifaccio:
lo rifaccio:
Trovare il centro, il raggio di convergenza e l'insieme di convergenza della serie
$\sum_{n=0}^∞ sqrt(n)(2x-5)^(2n)$
svolgimento:
metto il 2 in evidenza e lo porto fuori dalla parentesi:
$\sum_{n=0}^∞ sqrt(n)4^n(x-5/2)^(2n)$
centro = $5/2$
pongo y = $(x-5/2)^2$
diventa $\sum_{n=0}^∞ sqrt(n)4^n*y^(n)$
calcolo il raggio di convergenza:
$lim_(n->∞)(sqrt(n+1)*4^(n+1))/(sqrt(n)*4^n)$ = 4 ---> raggio di convergenza = $1/4$
l'insieme di convergenza si ottiene da $(x-5/2)^2 < 1/4$
quindi insieme di convergenza = $(2,3)$
per x = 2 e x = 3 la serie diverge
 lo rifaccio:
lo rifaccio:Trovare il centro, il raggio di convergenza e l'insieme di convergenza della serie
$\sum_{n=0}^∞ sqrt(n)(2x-5)^(2n)$
svolgimento:
metto il 2 in evidenza e lo porto fuori dalla parentesi:
$\sum_{n=0}^∞ sqrt(n)4^n(x-5/2)^(2n)$
centro = $5/2$
pongo y = $(x-5/2)^2$
diventa $\sum_{n=0}^∞ sqrt(n)4^n*y^(n)$
calcolo il raggio di convergenza:
$lim_(n->∞)(sqrt(n+1)*4^(n+1))/(sqrt(n)*4^n)$ = 4 ---> raggio di convergenza = $1/4$
l'insieme di convergenza si ottiene da $(x-5/2)^2 < 1/4$
quindi insieme di convergenza = $(2,3)$
per x = 2 e x = 3 la serie diverge
Ora va bene, ma lo svolgimento iniziale è fallato da alcuni gravi errori che, a futura memoria, ti spiego di seguito.
Innanzitutto, tieni presente che una s.d.p. è qualcosa del tipo \(\sum a_n (x-x_0)^n\) in cui figurano tutte le potenze di \(x-x_0\).
Nel caso del primo svolgimento sbagli sia a classificare la serie come s.d.p. (perché la base delle potenze, cioé \(2x-5\), non è nella forma \(x-x_0\)), sia a descrivere la successione dei coefficienti \(a_n\).
Questi errori, che si fanno molto di frequente, possono essere evitati con alcuni accorgimenti.
Ad esempio, scrivendo esplicitamente la sommatoria: infatti, scrivendo:
\[
\begin{split}
\sum_{n=0}^\infty \sqrt{n}\ (2x-5)^{2n} &= \sum_{n=0}^\infty \sqrt{n}\ 2^{2n}\ \left( x- \frac{5}{2}\right)^{2n}\\
&= 0 + (2x-5)^2 + \sqrt{2}\ (2x-5)^4 + 2\ (2x-5)^6+\cdots + \sqrt{n}\ (2x-5)^{2n} + \sqrt{n+1}\ (2x-5)^{2n+2}+\cdots
&= 0 + 4\ \left( x- \frac{5}{2}\right)^2 + 16\sqrt{2}\ \left( x- \frac{5}{2}\right)^4 + 128\ \left( x- \frac{5}{2}\right)^6 + \cdots + \sqrt{n}\ 2^{2n}\ \left( x- \frac{5}{2}\right)^{2n} + \sqrt{n+1}\ 2^{2n+2}\ \left( x- \frac{5}{2}\right)^{2n+2}+\cdots
\end{split}
\]
si vede che nella serie assegnata non compaiono tutte le potenze di \(x-5/2\), in quanto mancano le potenze dispari; perciò essa non si può classificare sic et simpliciter come serie di potenze.
Tuttavia, introducendo alcuni coefficienti nulli, è possibile scrivere:
\[
\begin{split}
\sum_{n=0}^\infty \sqrt{n}\ (2x-5)^{2n} &= 0 + \color{maroon}{0\ \left( x- \frac{5}{2}\right)} + 4\ \left( x- \frac{5}{2}\right)^2 + \color{maroon}{0\ \left( x- \frac{5}{2}\right)^3} + 16\sqrt{2}\ \left( x- \frac{5}{2}\right)^4 + \color{maroon}{0\ \left( x- \frac{5}{2}\right)^5} + 128\ \left( x- \frac{5}{2}\right)^6 + \cdots + \sqrt{n}\ 2^{2n}\ \left( x- \frac{5}{2}\right)^{2n} +\color{maroon}{0\ \left( x- \frac{5}{2}\right)^{2n+1}} + \sqrt{n+1}\ 2^{2n+2}\ \left( x- \frac{5}{2}\right)^{2n+2}+\cdots\\
&= \sum_{k=0}^\infty a_k\ \left( x- \frac{5}{2}\right)^k
\end{split}
\]
con:
\[
\tag{1}
a_k:= \begin{cases} \sqrt{n}\ 2^{2n} &\text{, se } k=2n \text{ (cioé se } k \text{ è pari)}\\
0 &\text{, se } k=2n+1 \text{ (cioé se } k \text{ è dispari)}.
\end{cases}
\]
L'ultima serie scritta, cioé \(\sum a_k (x-5/2)^k\), è nella "forma canonica" in cui si scrivono le serie di potenze ed è una serie del tutto equivalente a quella assegnata (nel senso che ne conserva la somma e l'insieme di convergenza).
Quindi, se si vuole classificare la serie assegnata come s.d.p. bisogna necessariamente riscriverla nel modo \(\sum a_k (x-5/2)^k\) con i coefficienti \(a_k\) dati dalle (1).
Tuttavia, operare con una s.d.p. in cui figurano infiniti coefficienti nulli è "difficile"[nota]Per far capire la difficoltà, illustro brevemente il procedimento che si dovrebbe usare in questo caso.
Innanzitutto noto che ai coefficienti \(a_k\) non si può applicare il criterio del rapporto (poiché ci sono infiniti coefficienti nulli che finrebbero al denominatore della frazione \(|a_{k+1}|/|a_k|\)), quindi bisogna usare necessariamente il criterio della radice per calcolare il raggio di convergenza della serie (il cui centro, ça va sans dire, è \(x_0=5/2\)).
Dunque si ha:
\[
\begin{split}
\sqrt[k]{|a_k|} &= \begin{cases} \sqrt[2n]{\sqrt{n}\ 2^{2n}} &\text{, se } k=2n \text{ (cioé se } k \text{ è pari)}\\
\sqrt[2n+1]{0} &\text{, se } k=2n+1 \text{ (cioé se } k \text{ è dispari)}
\end{cases}\\
&= \begin{cases} 2\ n^{\frac{1}{4n}} &\text{, se } k=2n \text{ (cioé se } k \text{ è pari)}\\
0 &\text{, se } k=2n+1 \text{ (cioé se } k \text{ è dispari)}
\end{cases}
\end{split}
\]
e si vede che la successione \(\sqrt[k]{|a_k|}\) non ha limite (infatti, l'estratta con indici dispari è costantemente uguale a \(0\) e perciò tende a \(0\), mentre l'estratta con indici pari è \(2\ n^{\frac{1}{4n}}\) e tende a \(2\)); tuttavia, una versione più generale del criterio della radice, che va sotto il nome di Teorema di Cauchy-Hadamard, garantisce che:
\[
\frac{1}{\rho} = \limsup_{k\to \infty} \sqrt[k]{|a_k|}
\]
ossia che nel caso in esame si ha:
\[
\frac{1}{\rho} = 2\qquad \Rightarrow \qquad \rho = \frac{1}{2}\; ,
\]
sicché l'intervallo di convergenza è \(]5/2-1/2 , 5/2+1/2[=]2,3[\), con intervallo aperto perchè non c'è convergenza negli estremi (come si verifica per sostituzione).[/nota], quindi è preferibile adottare un'altra tattica, che è quella della sostituzione (da te usata correttamente nel secondo svolgimento).
In altri termini, si nota che la serie assegnata è riconducibile ad una s.d.p. con centro in \(0\) usando la sostituzione \(y=(2x-5)^2\); della serie ausiliaria, cioé \(\sum \sqrt{n}\ y^n\), è facilissimo calcolare il raggio di convergenza e l'insieme di convergenza, in quanto si vede che \(\rho =1\) e la serie converge in \(]-1,1[\). Per determinare l'insieme di convergenza della serie assegnata, basta usare "a ritroso" la sostituzione di variabile: infatti, se la serie ausiliaria converge per \(-1
Spero di essere stato chiaro. Se hai dubbi, ne riparliamo.
Per gli altri esercizi, dammi il tempo di leggerli.
Innanzitutto, tieni presente che una s.d.p. è qualcosa del tipo \(\sum a_n (x-x_0)^n\) in cui figurano tutte le potenze di \(x-x_0\).
Nel caso del primo svolgimento sbagli sia a classificare la serie come s.d.p. (perché la base delle potenze, cioé \(2x-5\), non è nella forma \(x-x_0\)), sia a descrivere la successione dei coefficienti \(a_n\).
Questi errori, che si fanno molto di frequente, possono essere evitati con alcuni accorgimenti.
Ad esempio, scrivendo esplicitamente la sommatoria: infatti, scrivendo:
\[
\begin{split}
\sum_{n=0}^\infty \sqrt{n}\ (2x-5)^{2n} &= \sum_{n=0}^\infty \sqrt{n}\ 2^{2n}\ \left( x- \frac{5}{2}\right)^{2n}\\
&= 0 + (2x-5)^2 + \sqrt{2}\ (2x-5)^4 + 2\ (2x-5)^6+\cdots + \sqrt{n}\ (2x-5)^{2n} + \sqrt{n+1}\ (2x-5)^{2n+2}+\cdots
&= 0 + 4\ \left( x- \frac{5}{2}\right)^2 + 16\sqrt{2}\ \left( x- \frac{5}{2}\right)^4 + 128\ \left( x- \frac{5}{2}\right)^6 + \cdots + \sqrt{n}\ 2^{2n}\ \left( x- \frac{5}{2}\right)^{2n} + \sqrt{n+1}\ 2^{2n+2}\ \left( x- \frac{5}{2}\right)^{2n+2}+\cdots
\end{split}
\]
si vede che nella serie assegnata non compaiono tutte le potenze di \(x-5/2\), in quanto mancano le potenze dispari; perciò essa non si può classificare sic et simpliciter come serie di potenze.
Tuttavia, introducendo alcuni coefficienti nulli, è possibile scrivere:
\[
\begin{split}
\sum_{n=0}^\infty \sqrt{n}\ (2x-5)^{2n} &= 0 + \color{maroon}{0\ \left( x- \frac{5}{2}\right)} + 4\ \left( x- \frac{5}{2}\right)^2 + \color{maroon}{0\ \left( x- \frac{5}{2}\right)^3} + 16\sqrt{2}\ \left( x- \frac{5}{2}\right)^4 + \color{maroon}{0\ \left( x- \frac{5}{2}\right)^5} + 128\ \left( x- \frac{5}{2}\right)^6 + \cdots + \sqrt{n}\ 2^{2n}\ \left( x- \frac{5}{2}\right)^{2n} +\color{maroon}{0\ \left( x- \frac{5}{2}\right)^{2n+1}} + \sqrt{n+1}\ 2^{2n+2}\ \left( x- \frac{5}{2}\right)^{2n+2}+\cdots\\
&= \sum_{k=0}^\infty a_k\ \left( x- \frac{5}{2}\right)^k
\end{split}
\]
con:
\[
\tag{1}
a_k:= \begin{cases} \sqrt{n}\ 2^{2n} &\text{, se } k=2n \text{ (cioé se } k \text{ è pari)}\\
0 &\text{, se } k=2n+1 \text{ (cioé se } k \text{ è dispari)}.
\end{cases}
\]
L'ultima serie scritta, cioé \(\sum a_k (x-5/2)^k\), è nella "forma canonica" in cui si scrivono le serie di potenze ed è una serie del tutto equivalente a quella assegnata (nel senso che ne conserva la somma e l'insieme di convergenza).
Quindi, se si vuole classificare la serie assegnata come s.d.p. bisogna necessariamente riscriverla nel modo \(\sum a_k (x-5/2)^k\) con i coefficienti \(a_k\) dati dalle (1).
Tuttavia, operare con una s.d.p. in cui figurano infiniti coefficienti nulli è "difficile"[nota]Per far capire la difficoltà, illustro brevemente il procedimento che si dovrebbe usare in questo caso.
Innanzitutto noto che ai coefficienti \(a_k\) non si può applicare il criterio del rapporto (poiché ci sono infiniti coefficienti nulli che finrebbero al denominatore della frazione \(|a_{k+1}|/|a_k|\)), quindi bisogna usare necessariamente il criterio della radice per calcolare il raggio di convergenza della serie (il cui centro, ça va sans dire, è \(x_0=5/2\)).
Dunque si ha:
\[
\begin{split}
\sqrt[k]{|a_k|} &= \begin{cases} \sqrt[2n]{\sqrt{n}\ 2^{2n}} &\text{, se } k=2n \text{ (cioé se } k \text{ è pari)}\\
\sqrt[2n+1]{0} &\text{, se } k=2n+1 \text{ (cioé se } k \text{ è dispari)}
\end{cases}\\
&= \begin{cases} 2\ n^{\frac{1}{4n}} &\text{, se } k=2n \text{ (cioé se } k \text{ è pari)}\\
0 &\text{, se } k=2n+1 \text{ (cioé se } k \text{ è dispari)}
\end{cases}
\end{split}
\]
e si vede che la successione \(\sqrt[k]{|a_k|}\) non ha limite (infatti, l'estratta con indici dispari è costantemente uguale a \(0\) e perciò tende a \(0\), mentre l'estratta con indici pari è \(2\ n^{\frac{1}{4n}}\) e tende a \(2\)); tuttavia, una versione più generale del criterio della radice, che va sotto il nome di Teorema di Cauchy-Hadamard, garantisce che:
\[
\frac{1}{\rho} = \limsup_{k\to \infty} \sqrt[k]{|a_k|}
\]
ossia che nel caso in esame si ha:
\[
\frac{1}{\rho} = 2\qquad \Rightarrow \qquad \rho = \frac{1}{2}\; ,
\]
sicché l'intervallo di convergenza è \(]5/2-1/2 , 5/2+1/2[=]2,3[\), con intervallo aperto perchè non c'è convergenza negli estremi (come si verifica per sostituzione).[/nota], quindi è preferibile adottare un'altra tattica, che è quella della sostituzione (da te usata correttamente nel secondo svolgimento).
In altri termini, si nota che la serie assegnata è riconducibile ad una s.d.p. con centro in \(0\) usando la sostituzione \(y=(2x-5)^2\); della serie ausiliaria, cioé \(\sum \sqrt{n}\ y^n\), è facilissimo calcolare il raggio di convergenza e l'insieme di convergenza, in quanto si vede che \(\rho =1\) e la serie converge in \(]-1,1[\). Per determinare l'insieme di convergenza della serie assegnata, basta usare "a ritroso" la sostituzione di variabile: infatti, se la serie ausiliaria converge per \(-1
Spero di essere stato chiaro. Se hai dubbi, ne riparliamo.
Per gli altri esercizi, dammi il tempo di leggerli.
GRAZIE MILLE!
Lei è stato chiaro, efficace e pefetto nella sua spiegazione



p.s.
usare il TeX non è poi cosi difficile
Lei è stato chiaro, efficace e pefetto nella sua spiegazione



p.s.
usare il TeX non è poi cosi difficile
"androidiano":
GRAZIE MILLE!
Lei è stato chiaro, efficace e pefetto nella sua spiegazione


Prego.
Ma qui non siamo in università, quindi ci si dà del tu.
"androidiano":
p.s.: usare il TeX non è poi cosi difficile
Come ovvio che sia. Dato che lo usano un po' tutti per scrivere la Matematica non può essere così difficile.
Per gli altri esercizi, il primo è fatto bene con le correzioni che hai già postato.
La determinazione dell'insieme di convergenza si semplifica procedendo come segue. Scrivere \(-1/2
La convergenza negli estremi c'è solo in \(x=-1\).
Il secondo pure è svolto bene.
Ecco un'altra delle risposte-capolavoro di Gugo.
"Tanto di cappello" per la tua dedizione e bravura.
"Tanto di cappello" per la tua dedizione e bravura.
e adesso... serie di Fourier 


Partiamo dai concetti base: in natura esistono fenomeni (onde acustiche, vibrazioni ecc.) caratterizzati da una funzione periodica, la serie di Fourier ci consente di approssimarle utilizzando seno e coseno attraverso i polinomi trigonometrici:
f(x) = $a_o/2$ + $\sum_{k=1}^n (a_kcos(kx) + b_ksin(kx))$
Quindi per scrivere la serie devo determinare i coefficienti $a_0, a_k, b_k$
$a_0$ = $1/π$ $\int_-π^πf(x)dx$
$a_k$ = $1/π$ $\int_-π^πf(x)cos(kx)dx$
$b_k$ = $1/π$ $\int_-π^πf(x)sin(kx)dx$
domanda 1:
l'intervallo può essere uno qualsiasi di ampiezza 2π quindi anche [0, 2π] giusto?
domanda 2:
Se la funzione è pari [f(x) = f(-x)] allora $b_k$ = 0
Se la funzione è dispari [f(x) = -f(-x)] $a_k$ = 0
quindi se mi accorgo che la funzione è pari o dispari posso evitare di calcolare rispettivamente $b_k$ e $a_k$ ?
domanda 3:
Se la funzione è periodica ma non di periodo 2π come si calcolano $a_0$ $a_k$ $b_k$ ?
Ho provato a fare questo esercizio:
$g(x)={(x, se -π$<=$x$<$0)}$
$g(x)={(1, 0$<=$x$<$π)}$
(a) disegnare il grafico di f(x) prolungamento periodico di g
(b) Calcolare la serie di Fourier associata a f
(c) Studiare la convergenza in R della serie
(d) Calcolare la somma della serie per x = 1/2
(a) il grafico l'ho disegnato ma non so come postarlo qui
(b)
$a_0$ = $(2-π)/2$
$a_k$ = 0
$b_k$ = $1/π$( $\int_{-\pi}^{0} xsin(kx) dx$ + $\int_{0}^{\pi} xsin(kx) dx$ )
$b_k$ = $cos(kπ)/k$ = $(-1)^(k)/k$
quindi ho:
$(2-\pi)/4$ + $\sum_{k=1}^∞ (-1)^(k)/k sin(kx)$
(c)
è una serie a segni variabili posso studiare se c'è convergenza assoluta?
(d)
se sostituisco a x il valore 1/2 devo studiare un'ennesima serie numerica e vedere se converge?
Partiamo dai concetti base: in natura esistono fenomeni (onde acustiche, vibrazioni ecc.) caratterizzati da una funzione periodica, la serie di Fourier ci consente di approssimarle utilizzando seno e coseno attraverso i polinomi trigonometrici:
f(x) = $a_o/2$ + $\sum_{k=1}^n (a_kcos(kx) + b_ksin(kx))$
Quindi per scrivere la serie devo determinare i coefficienti $a_0, a_k, b_k$
$a_0$ = $1/π$ $\int_-π^πf(x)dx$
$a_k$ = $1/π$ $\int_-π^πf(x)cos(kx)dx$
$b_k$ = $1/π$ $\int_-π^πf(x)sin(kx)dx$
domanda 1:
l'intervallo può essere uno qualsiasi di ampiezza 2π quindi anche [0, 2π] giusto?
domanda 2:
Se la funzione è pari [f(x) = f(-x)] allora $b_k$ = 0
Se la funzione è dispari [f(x) = -f(-x)] $a_k$ = 0
quindi se mi accorgo che la funzione è pari o dispari posso evitare di calcolare rispettivamente $b_k$ e $a_k$ ?
domanda 3:
Se la funzione è periodica ma non di periodo 2π come si calcolano $a_0$ $a_k$ $b_k$ ?
Ho provato a fare questo esercizio:
$g(x)={(x, se -π$<=$x$<$0)}$
$g(x)={(1, 0$<=$x$<$π)}$
(a) disegnare il grafico di f(x) prolungamento periodico di g
(b) Calcolare la serie di Fourier associata a f
(c) Studiare la convergenza in R della serie
(d) Calcolare la somma della serie per x = 1/2
(a) il grafico l'ho disegnato ma non so come postarlo qui
(b)
$a_0$ = $(2-π)/2$
$a_k$ = 0
$b_k$ = $1/π$( $\int_{-\pi}^{0} xsin(kx) dx$ + $\int_{0}^{\pi} xsin(kx) dx$ )
$b_k$ = $cos(kπ)/k$ = $(-1)^(k)/k$
quindi ho:
$(2-\pi)/4$ + $\sum_{k=1}^∞ (-1)^(k)/k sin(kx)$
(c)
è una serie a segni variabili posso studiare se c'è convergenza assoluta?
(d)
se sostituisco a x il valore 1/2 devo studiare un'ennesima serie numerica e vedere se converge?
"androidiano":
Partiamo dai concetti base: in natura esistono fenomeni (onde acustiche, vibrazioni ecc.) caratterizzati da una funzione periodica, la serie di Fourier ci consente di approssimarle utilizzando seno e coseno attraverso i polinomi trigonometrici:
f(x) = $a_o/2$ + $\sum_{k=1}^n (a_kcos(kx) + b_ksin(kx))$
Quindi per scrivere la serie devo determinare i coefficienti $a_0, a_k, b_k$
$a_0$ = $1/π$ $\int_-π^πf(x)dx$
$a_k$ = $1/π$ $\int_-π^πf(x)cos(kx)dx$
$b_k$ = $1/π$ $\int_-π^πf(x)sin(kx)dx$
domanda 1:
l'intervallo può essere uno qualsiasi di ampiezza 2π quindi anche [0, 2π] giusto?
Se la funzione ha periodo \(2\pi\), sì può essere un qualsiasi intervallo di periodicità (ad esempio, anche \([1,1+2\pi[\)).
"androidiano":
domanda 2:
Se la funzione è pari [f(x) = f(-x)] allora $b_k$ = 0
Se la funzione è dispari [f(x) = -f(-x)] $a_k$ = 0
quindi se mi accorgo che la funzione è pari o dispari posso evitare di calcolare rispettivamente $b_k$ e $a_k$ ?
Ovvio, perché in ognuno dei due casi sai già che parte dei coefficienti sono nulli.
"androidiano":
domanda 3:
Se la funzione è periodica ma non di periodo 2π come si calcolano $a_0$ $a_k$ $b_k$ ?
Ad esempio, prendiamo una funzione \(f(x)\) periodica di periodo \(T>0\) e vediamo come fare a determinarne i coefficienti di Fourier.
Consideriamo la funzione ausiliaria \(g(y)\) definita ponendo:
\[
g(y) := f\left( \frac{T}{2\pi} y\right)\; ;
\]
tale funzione è periodica di periodo \(2\pi\), poiché per fissato \(y\) risulta:
\[
g(y+2k\pi) = f\left( \frac{T}{2\pi} (y+2k\pi)\right) = \underbrace{f\left( \frac{T}{2\pi} y + kT\right) = f\left( \frac{T}{2\pi} y\right)}_{\text{periodicità di } f} =g(y)
\]
per ogni \(k\in \mathbb{Z}\).
I coefficienti di Fourier di \(g(y)\), chiamiamoli \(\alpha_k\) e \(\beta_k\), sono dati da:
\[
\begin{split}
\alpha_0 &= \frac{1}{\pi}\ \int_{-pi}^\pi g(y)\ \text{d} y\\
&= \frac{1}{\pi}\ \int_{-\pi}^\pi f\left( \frac{T}{2\pi} y\right)\ \text{d} y\\
&\stackrel{x=\frac{T}{2\pi} y}{=} \frac{1}{\pi}\ \int_{-T/2}^{T/2} f(x)\ \frac{2\pi}{T}\ \text{d} x\\
&= \frac{2}{T}\ \int_{-T/2}^{T/2} f(x)\ \text{d} x\\
\alpha_k &= \frac{1}{\pi}\ \int_{-\pi}^\pi g(y)\ \cos (ky)\ \text{d} y\\
&= \frac{1}{\pi}\ \int_{-\pi}^\pi f\left( \frac{T}{2\pi} y\right)\ \cos (ky)\ \text{d} y\\
&\stackrel{x=\frac{T}{2\pi} y}{=} \frac{1}{\pi}\ \int_{-T/2}^{T/2} f(x)\ \cos \left( \frac{2k\pi}{T}\ x\right)\ \frac{2\pi}{T}\ \text{d} x\\
&= \frac{2}{T}\ \int_{-T/2}^{T/2} f(x)\ \cos \left( \frac{2k\pi}{T}\ x\right)\ \text{d} x
\end{split}
\]
ed allo stesso modo si trova:
\[
\begin{split}
\beta_k &= \frac{1}{\pi}\ \int_{-\pi}^\pi g(y)\ \sin (ky)\ \text{d} y\\
&= \frac{1}{\pi}\ \int_{-\pi}^\pi f\left( \frac{T}{2\pi} x\right)\ \sin (ky)\ \text{d} y\\
&\stackrel{x=\frac{T}{2\pi} y}{=} \frac{1}{\pi}\ \int_{-T/2}^{T/2} f(x)\ \sin \left( \frac{2k\pi}{T}\ x\right)\ \frac{2\pi}{T}\ \text{d} x\\
&= \frac{2}{T}\ \int_{-T/2}^{T/2} f(x)\ \sin \left( \frac{2k\pi}{T}\ x\right)\ \text{d} x\\
\end{split}
\]
cosicché risulta:
\[
g(y) = \frac{\alpha_0}{2} + \sum_{k=1}^\infty \alpha_k\ \cos (k y) + \beta_k\ \sin (ky)
\]
ossia:
\[
f\left( \frac{T}{2\pi}\ y\right) = \frac{\alpha_0}{2} + \sum_{k=1}^\infty \alpha_k\ \cos (k y) + \beta_k\ \sin (ky)\; .
\]
Lo sviluppo in serie di Fourier di \(f\) si ottiene sostituendo \(x=\frac{T}{2\pi} y\) nell'ultima uguaglianza precedente e si ottiene:
\[
f(x) = \frac{\alpha_0}{2} + \sum_{k=1}^\infty \alpha_k\ \cos \left( \frac{2\pi}{T} x\right) + \beta_k\ \sin \left( \frac{2\pi}{T} x\right)
\]
in cui i coefficienti sono quelli calcolati sopra, cioé:
\[
\begin{split}
\alpha_k &= \frac{2}{T}\ \int_{-T/2}^{T/2} f(x)\ \cos \left( \frac{2k\pi}{T}\ x\right)\ \text{d} x\\
\beta_k &= \frac{2}{T}\ \int_{-T/2}^{T/2} f(x)\ \sin \left( \frac{2k\pi}{T}\ x\right)\ \text{d} x\; .
\end{split}
\]
Nota bene: quando cambia il periodo cambiano anche le armoniche nello sviluppo di Fourier, cioé al posto di \(\cos k x\) e \(\sin k x\) si trovano le funzioni \( \cos \left( \frac{2k\pi}{T}\ x\right)\) e \( \sin \left( \frac{2k\pi}{T}\ x\right)\).
grazie 

nel rivedere l'esercizio che ho postato mi sono accorto di aver commesso qualche errore di calcolo, ho rifatto l'esercizio ma mi ritrovo con $a_0$ semplice, $a_k$ accettabile e $b_k$ mostruoso
$a_0$ = $(2-π)/2$
$a_k$ = $(1-(-1)^k)/(π*k^2)$
$b_k$ = $(-kπ(-1)^(k)+k-k(-1)^(k))/(π*k^2)$
questa volta non penso di aver commesso altri errori di calcolo, ho paura a scrivere la serie di Fourier con questi coefficienti e sopratutto ho ancora più paura a
c) Studiare la convergenza in R della serie
(d) Calcolare la somma della serie per x = 1/2







nel rivedere l'esercizio che ho postato mi sono accorto di aver commesso qualche errore di calcolo, ho rifatto l'esercizio ma mi ritrovo con $a_0$ semplice, $a_k$ accettabile e $b_k$ mostruoso
$a_0$ = $(2-π)/2$
$a_k$ = $(1-(-1)^k)/(π*k^2)$
$b_k$ = $(-kπ(-1)^(k)+k-k(-1)^(k))/(π*k^2)$
questa volta non penso di aver commesso altri errori di calcolo, ho paura a scrivere la serie di Fourier con questi coefficienti e sopratutto ho ancora più paura a
c) Studiare la convergenza in R della serie
(d) Calcolare la somma della serie per x = 1/2
"androidiano":
Ho provato a fare questo esercizio:
$g(x)={(x, se -π$<=$x$<$0)}$
$g(x)={(1, 0$<=$x$<$π)}$
(a) disegnare il grafico di f(x) prolungamento periodico di g
(b) Calcolare la serie di Fourier associata a f
(c) Studiare la convergenza in R della serie
(d) Calcolare la somma della serie per x = 1/2
(a) il grafico l'ho disegnato ma non so come postarlo qui
(b)
$a_0$ = $(2-π)/2$
$a_k$ = 0
$b_k$ = $1/π$( $\int_{-\pi}^{0} xsin(kx) dx$ + $\int_{0}^{\pi} xsin(kx) dx$ )
$b_k$ = $cos(kπ)/k$ = $(-1)^(k)/k$
quindi ho:
$(2-\pi)/4$ + $\sum_{k=1}^∞ (-1)^(k)/k sin(kx)$
(c)
è una serie a segni variabili posso studiare se c'è convergenza assoluta?
(d)
se sostituisco a x il valore 1/2 devo studiare un'ennesima serie numerica e vedere se converge?
Il grafico dovrebbe essere questo:
[asvg]xmin=-7; xmax=7;
axes("","");
stroke="red"; strokewidth=2;
line([-3.141, -3.141] , [0,0]); line([0,1] , [3.141,1]);
stroke="dodgerblue";
line([-9.423,-3.141] , [-6.282,0]); line([-6.282,1] , [-3.141,1]); line([9.423,1] , [6.282,1]); line([6.282,0] , [3.141,-3.141]);[/asvg]
e da qui si vede che l'estensione periodica non è né pari né dispari; ergo i coefficienti della s.d.F. vanno calcolati tutti.
Si ha:
\[
\begin{split}
a_0 &= \frac{1}{\pi}\ \int_{-\pi}^\pi g(x)\ \text{d} x\\
&= \frac{1}{\pi}\ \left( \int_{-\pi}^0 x\ \text{d} x + \int_0^\pi 1\ \text{d} x\right)\\
&= \frac{1}{\pi}\ \left( -\frac{\pi^2}{2} + \pi\right)\\
&= \frac{2-\pi}{2}\\
a_k &= \frac{1}{\pi}\ \int_{-\pi}^\pi g(x)\ \cos (kx)\ \text{d} x\\
&= \frac{1}{\pi}\ \left( \int_{-\pi}^0 x\ \cos (kx)\ \text{d} x + \int_0^\pi \cos (kx) \text{d} x\right)\\
&= \frac{1}{\pi}\ \left( \frac{1}{k}\ x\ \sin (kx)\Big|_{-\pi}^0 - \frac{1}{k}\ \int_{-\pi}^0 \sin (kx)\ \text{d} x + \frac{1}{k}\ \sin (kx)\Big|_0^\pi \text{d} x\right)\\
&= \frac{1}{\pi}\ \left( - \frac{1}{k}\ \int_{-\pi}^0 \sin (kx)\ \text{d} x \right)\\
&= \frac{1}{\pi}\ \left( \frac{1}{k^2}\ \cos (kx)\Big|_{-\pi}^0\right)\\
&= \frac{1}{\pi\ k^2}\ \left( 1-\cos (-k\pi)\right)\\
&= \frac{1}{\pi\ k^2}\ \left( 1-\cos (k\pi)\right)\\
&= \frac{1}{\pi\ k^2}\ \left( 1-(-1)^k\right)
\end{split}
\]
ed allo stesso modo:
\[
\begin{split}
b_k &= \frac{1}{\pi}\ \int_{-\pi}^\pi g(x)\ \sin (kx)\ \text{d} x\\
&= \frac{1}{\pi}\ \left( \int_{-\pi}^0 x\ \sin (kx)\ \text{d} x + \int_0^\pi \sin (kx) \text{d} x\right)\\
&= \frac{1}{\pi}\ \left( -\frac{1}{k}\ x\ \cos (kx)\Big|_{-\pi}^0 + \frac{1}{k}\ \int_{-\pi}^0 \cos (kx)\ \text{d} x - \frac{1}{k}\ \cos (kx)\Big|_0^\pi \text{d} x\right)\\
&= \frac{1}{\pi}\ \left( -\frac{\pi}{k}\ \cos (-k\pi) +\frac{1}{k^2} \sin (kx)\Big|_{-\pi}^0 - \frac{1}{k}\ (cos(k\pi) -1) \right)\\
&= \frac{1}{\pi}\ \left( -\frac{\pi}{k}\ (-1)^k - \frac{1}{k}\ ((-1)^k - 1)\right)\\
&= \frac{1}{\pi\ k}\ \left( 1- (-1)^k (\pi +1)\right)\; .
\end{split}
\]
Quindi:
\[
\frac{2-\pi}{4} + \sum_{k=1}^\infty \frac{1}{\pi\ k^2}\ \left( 1-(-1)^k\right)\ \cos (kx) + \frac{1}{\pi\ k}\ \left( 1- (-1)^k (\pi +1)\right)\ \sin (k x)\; ,
\]
è la serie di Fourier cercata (se non ho sbagliato i conti...
Per noti fatti sulle serie di Fourier (leggi, per le condizioni di Dirichlet), la s.d.F. converge verso la funzione definita ponendo:
\[
\frac{f(x^+)+f(x^-)}{2}\; ,
\]
in cui:
\[
f(x^\pm) := \lim_{t\to x^\pm} f(t)\; .
\]
Pertanto, la serie determinata sopra converge verso \(f(x)\) in tutti i punti in cui la \(f\) è continua, cioé in tutti i punti distinti da \(x_n:=n\pi\) con \(n\in \mathbb{Z}\); d'altra parte, la serie converge verso:
\[
\frac{f(0^+)+f(0^-)}{2} = \frac{1+0}{2} = \frac{1}{2}
\]
in ogni punto del tipo \(x_{2n}=2n\pi\) con \(n\in \mathbb{Z}\), mentre converge verso:
\[
\frac{f(\pi^+)+f(\pi^-)}{2} = \frac{f(-\pi^+)+f(\pi^-)}{2} = \frac{-\pi + 1}{2} = \frac{1-\pi}{2}\approx -1.0708
\]
nei punti \(x_{2n+1}=(2n+1)\pi\) con \(n\in \mathbb{Z}\).
Ne consegue che per \(x=1/2 \in [0,\pi[\), la s.d.F. converge verso \(f(1/2)=1\), ossia che risulta:
\[
\begin{split}
1 &= \frac{2-\pi}{4} + \sum_{k=1}^\infty \frac{1}{\pi\ k^2}\ \left( 1-(-1)^k\right)\ \cos (k/2) + \frac{1}{\pi\ k}\ \left( 1- (-1)^k (\pi +1)\right)\ \sin (k /2)
\end{split}
\]
(sempre ammesso e non concesso che non abbia sbagliato i conti...
$a_0$ e $a_k$ mi trovo  $b_k$ pensavo di averlo sbagliato ma è giusto pure questo
$b_k$ pensavo di averlo sbagliato ma è giusto pure questo 
quando finalmente scrivo la serie di Fourier noto che ci sono alcuni $(-1)^k ora poiché k può essere pari o dispari quando k e pari la serie dovrebbe semplificarsi, mi conviene distinguere i casi tra k pari e dispari?
GRAZIE 10! per l'aiuto


 $b_k$ pensavo di averlo sbagliato ma è giusto pure questo
$b_k$ pensavo di averlo sbagliato ma è giusto pure questo 
quando finalmente scrivo la serie di Fourier noto che ci sono alcuni $(-1)^k ora poiché k può essere pari o dispari quando k e pari la serie dovrebbe semplificarsi, mi conviene distinguere i casi tra k pari e dispari?
GRAZIE 10! per l'aiuto


Oddio, queste pagine salveranno il mio esame di analisi!
Quindi riepilogando la serie non converge uniformemente perché f non è continua, converge puntualmente a f(x) per ogni x dove f è definita (es. a $1/2$ converge a 1)
nei punti in cui non è continua converge puntualmente a \[
\frac{f(x^+)+f(x^-)}{2}\;
\]
giusto?
nei punti in cui non è continua converge puntualmente a \[
\frac{f(x^+)+f(x^-)}{2}\;
\]
giusto?
Yes.
CURVE
1)
Nello studio delle curve per dimostrare che una curva $\gamma$ è regolare:
calcolo $\gamma$' e verifico che le sue componenti sono funzioni $C^1$ (cioè che hanno derivata?)
il vettore che ha come componenti quelle di $\gamma$' deve essere diverso dal vettore nullo (0, 0, ... 0) questa cosa la posso verificare calcolando la norma al quadrato del vettore che deve essere diversa da zero
2)
dimostrare che una curva è semplice non lo è affatto! Perdonate il gioco di parole ma ci sono casi abbastanza difficili, qualche consiglio?
1)
Nello studio delle curve per dimostrare che una curva $\gamma$ è regolare:
calcolo $\gamma$' e verifico che le sue componenti sono funzioni $C^1$ (cioè che hanno derivata?)
il vettore che ha come componenti quelle di $\gamma$' deve essere diverso dal vettore nullo (0, 0, ... 0) questa cosa la posso verificare calcolando la norma al quadrato del vettore che deve essere diversa da zero
2)
dimostrare che una curva è semplice non lo è affatto! Perdonate il gioco di parole ma ci sono casi abbastanza difficili, qualche consiglio?
Quando devo calcolare il limite di funzioni a 2 variabili posso usare 2 metodi:
1) y = mx diventa il limite per x->0 nella sola variabile x se il risultato del limite dipende da m allora il limite non esiste perché non è univoco (il limite se esiste è unico), ma se mi viene un numero es: 5 il limite esiste e vale 5? Oppure devo provare in altri modi?
2) coordinate polari x = $\rho$ $cos$ $\vartheta$ y = $\rho$ $sin$$\vartheta$ sostituendo se mi viene un valore che dipende da $\vartheta$ il limite non esiste.
Quando posso dire che un limite di due variabili esiste?
1) y = mx diventa il limite per x->0 nella sola variabile x se il risultato del limite dipende da m allora il limite non esiste perché non è univoco (il limite se esiste è unico), ma se mi viene un numero es: 5 il limite esiste e vale 5? Oppure devo provare in altri modi?
2) coordinate polari x = $\rho$ $cos$ $\vartheta$ y = $\rho$ $sin$$\vartheta$ sostituendo se mi viene un valore che dipende da $\vartheta$ il limite non esiste.
Quando posso dire che un limite di due variabili esiste?




 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo