Una sommatoria alternante di quadrati, cubi, etc.
Qualcuno mi dice quanto fa
0-1+4-9+16-25+36-49+.... ?
cioè quanto fa per un $N$ qualsiasi
$\sum_0^N(-)^kk^2$ ?
Vorrei una dimostrazione e non solo il risultato brutale.
E, per favore, niente uso del principio di induzione finita!
Faccio notare intanto che
$\sum_0^N(-)^kk=(-)^N (N+1)|2$ dove a\b indica "divisione intera" di a per b
0-1+4-9+16-25+36-49+.... ?
cioè quanto fa per un $N$ qualsiasi
$\sum_0^N(-)^kk^2$ ?
Vorrei una dimostrazione e non solo il risultato brutale.
E, per favore, niente uso del principio di induzione finita!
Faccio notare intanto che
$\sum_0^N(-)^kk=(-)^N (N+1)|2$ dove a\b indica "divisione intera" di a per b
Risposte
Evidentemente si può partire da k=1.Occorre distinguere i casi N pari ed N dispari.
a) N=2m
Indicando con S la somma richiesta risulta:
$S=(2^2-1^2)+(4^2-3^2)+(6^2-5^2)+....+((2m)^2-(2m-1)^2)$
Ovvero :
$S=(2-1)(2+1)+(4-3)(4+3)+(6-5)(6+5)+....+(2m-2m+1)((2m+2m-1)$
Cioé:
$S=3+7+4+11+....+(4m-1)=(3+4m-1)/2*m=m(2m+1)$
ed in conclusione per N pari si ottiene il risultato:
$S=(N(N+1))/2$
b) N=2m+1
Si ha :
$S=sum_(k=1)^(2m+1)(-1)^k k^2=sum_(k=1)^(2m)(-1)^k k^2-(2m+1)^2=m(2m+1)-(2m+1)^2=-(2m+1)(m+1)$
ed in conclusione per N dispari si ha:
$S=-(N(N+1))/2$
P.S.
Dovresti essere un po' meno...ultimativo nelle tue richieste

a) N=2m
Indicando con S la somma richiesta risulta:
$S=(2^2-1^2)+(4^2-3^2)+(6^2-5^2)+....+((2m)^2-(2m-1)^2)$
Ovvero :
$S=(2-1)(2+1)+(4-3)(4+3)+(6-5)(6+5)+....+(2m-2m+1)((2m+2m-1)$
Cioé:
$S=3+7+4+11+....+(4m-1)=(3+4m-1)/2*m=m(2m+1)$
ed in conclusione per N pari si ottiene il risultato:
$S=(N(N+1))/2$
b) N=2m+1
Si ha :
$S=sum_(k=1)^(2m+1)(-1)^k k^2=sum_(k=1)^(2m)(-1)^k k^2-(2m+1)^2=m(2m+1)-(2m+1)^2=-(2m+1)(m+1)$
ed in conclusione per N dispari si ha:
$S=-(N(N+1))/2$
P.S.
Dovresti essere un po' meno...ultimativo nelle tue richieste
Grazie assai per il tuo aiuto.
Quindi per N dispari o pari, non importa, la formula è
$S_2(N)-=\sum_0^N(-)^kk^2=(-)^N((N+1),(2))$
Giusto? E che dire di
$S_3(N)-=\sum_0^N(-)^kk^3$?
Hai qualche idea di come calcolarlo?
Nota che
$S_1(N)-=\sum_0^N(-)^kk=(-)^N (N+1)\\2$ dobe $a\\b$ indica "divisione intera di $a$ per $b$.
Ho intenzione anche di calcolare le quantità
$B_p(N)-=\sum_p^N(-)^k((k),(p))$ almeno per $p=2$ e $p=3$.
Per p=1 infatti si ha: $B_1(N) = S_1(N) $, che ho appena scritto 3 righe più su.
Per quanto riguarda $B_2(N)$ mi sembra che, a parte il solito fattore $(-)^N$, tale somma coincida in modulo con la somma di tutti i numeri dispari o pari, positivi e inferiori a N, a seconda che N sia, rispettivamente, pari o dispari.
Quindi per N dispari o pari, non importa, la formula è
$S_2(N)-=\sum_0^N(-)^kk^2=(-)^N((N+1),(2))$
Giusto? E che dire di
$S_3(N)-=\sum_0^N(-)^kk^3$?
Hai qualche idea di come calcolarlo?
Nota che
$S_1(N)-=\sum_0^N(-)^kk=(-)^N (N+1)\\2$ dobe $a\\b$ indica "divisione intera di $a$ per $b$.
Ho intenzione anche di calcolare le quantità
$B_p(N)-=\sum_p^N(-)^k((k),(p))$ almeno per $p=2$ e $p=3$.
Per p=1 infatti si ha: $B_1(N) = S_1(N) $, che ho appena scritto 3 righe più su.
Per quanto riguarda $B_2(N)$ mi sembra che, a parte il solito fattore $(-)^N$, tale somma coincida in modulo con la somma di tutti i numeri dispari o pari, positivi e inferiori a N, a seconda che N sia, rispettivamente, pari o dispari.
Illustrazione pittorica 
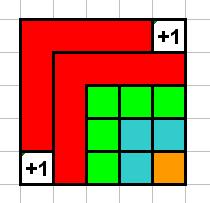
l'incremento di un quadrato è sempre uguale all'incremento del precedente (n-1) + 2
.... ma siccome i segni si invertono....

l'incremento di un quadrato è sempre uguale all'incremento del precedente (n-1) + 2
.... ma siccome i segni si invertono....

Per la somma dei cubi ci si può affidare alla formula $a^3-b^3=(a-b)(a^2+ab+b^2)$
Anche qui consideriamo due casi:
A)N=2m
Si ha allora ( le sommatorie sono tutte da 1 ad m):
$S=sum_k[(2k)^3-(2k-1)^3]=sum_k[(2k-2k+1)((2k)^2+(2k)(2k-1)+(2k-1)^2)]=sum_k(12k^2-6k+1)
Ovvero:
$S=12sum_kk^2-6sum_kk+m=12(m(m+1)(2m+1))/6-6(m(m+1))/2+m=m^2(4m+3)$
Tenuto conto che $m=N/2$,sostituendo abbiamo la formula:
$S=1/4N^2(2N+3)$
B)N=2m+1
$S=sum_(k=1)^(2m+1)[(2k)^3-(2k-1)^3]=sum_(k=1)^(2m)[(2k)^3-(2k-1)^3]-(2m+1)^3=m^2(4m+3)-(2m+1)^3$
Tenuto conto che in questo caso è $m=(N-1)/2$, sostituendo e facendo i calcoli si ha :
$S=-1/4N^2(2N+3)+1/4$
In conclusione si può scrivere un'unica formula :
$S=(-1)^N1/4N^2(2N+3)+1/4*epsilon_N$ dove è $epsilon_N=0 $ per N pari ed $epsilon_N=1 $ per N dispari
Anche qui consideriamo due casi:
A)N=2m
Si ha allora ( le sommatorie sono tutte da 1 ad m):
$S=sum_k[(2k)^3-(2k-1)^3]=sum_k[(2k-2k+1)((2k)^2+(2k)(2k-1)+(2k-1)^2)]=sum_k(12k^2-6k+1)
Ovvero:
$S=12sum_kk^2-6sum_kk+m=12(m(m+1)(2m+1))/6-6(m(m+1))/2+m=m^2(4m+3)$
Tenuto conto che $m=N/2$,sostituendo abbiamo la formula:
$S=1/4N^2(2N+3)$
B)N=2m+1
$S=sum_(k=1)^(2m+1)[(2k)^3-(2k-1)^3]=sum_(k=1)^(2m)[(2k)^3-(2k-1)^3]-(2m+1)^3=m^2(4m+3)-(2m+1)^3$
Tenuto conto che in questo caso è $m=(N-1)/2$, sostituendo e facendo i calcoli si ha :
$S=-1/4N^2(2N+3)+1/4$
In conclusione si può scrivere un'unica formula :
$S=(-1)^N1/4N^2(2N+3)+1/4*epsilon_N$ dove è $epsilon_N=0 $ per N pari ed $epsilon_N=1 $ per N dispari
Grazie della tua bella formula.
Non volendo seguire tutti i passaggi, l'ho sottoposta a verifica (col computer) e funziona (almeno per N=1,2,3,4, ..., 16).
Permettimi di riscriverla facendo uso della seguente notazione, alternativa al tuo $\epsilon_N$:
$ (N-:p)-=$resto della divisione di N per p. Allora
$\sum_0^N(-)^kk^3=\frac{(-)^N}{4}[N^2(2N+3)-(N-:2)]$
Ora voglio vedere Umby se, giocando coi cubetti di lato N, riesce ad illustrarci simpaticamente anche questa formula.
Non volendo seguire tutti i passaggi, l'ho sottoposta a verifica (col computer) e funziona (almeno per N=1,2,3,4, ..., 16).
Permettimi di riscriverla facendo uso della seguente notazione, alternativa al tuo $\epsilon_N$:
$ (N-:p)-=$resto della divisione di N per p. Allora
$\sum_0^N(-)^kk^3=\frac{(-)^N}{4}[N^2(2N+3)-(N-:2)]$
Ora voglio vedere Umby se, giocando coi cubetti di lato N, riesce ad illustrarci simpaticamente anche questa formula.
Per non essere da meno, ho trovato anch'io una bella formula:
Definisco $B_p(N)-=\sum_{k=p}^N(-)^k((k),(p))$
Allora $B_3(N)=\frac{(-)^N}{4!}[N(N-2)(2N+1)+3(N-:2)]$
Propongo infine due altre somme da esprimere in formula chiusa (e senza usare dei "se N è pari..." o "se N è dispari...")
$U_2(N)=(N-1)+(N-3)+(N-5) +...$ etc. fino a che l'addendo resta positivo
$V_4(N)=f(N-2)+f(N-6)+f(N-10)+f(N-14) + ...$ etc. fino a che l'addendo resta positivo, con $f(x)-=x^2-x+1$
Hint: Per la prima somma non servono suggerimenti (è una somma o di numeri tutti pari o tutti dispari), per la seconda dico che in questa pagina c'è già la risposta ....
Definisco $B_p(N)-=\sum_{k=p}^N(-)^k((k),(p))$
Allora $B_3(N)=\frac{(-)^N}{4!}[N(N-2)(2N+1)+3(N-:2)]$
Propongo infine due altre somme da esprimere in formula chiusa (e senza usare dei "se N è pari..." o "se N è dispari...")
$U_2(N)=(N-1)+(N-3)+(N-5) +...$ etc. fino a che l'addendo resta positivo
$V_4(N)=f(N-2)+f(N-6)+f(N-10)+f(N-14) + ...$ etc. fino a che l'addendo resta positivo, con $f(x)-=x^2-x+1$
Hint: Per la prima somma non servono suggerimenti (è una somma o di numeri tutti pari o tutti dispari), per la seconda dico che in questa pagina c'è già la risposta ....
"seascoli":
Ora voglio vedere Umby se, giocando coi cubetti di lato N, riesce ad illustrarci simpaticamente anche questa formula.
Se ho tempo, la farò con Photoshop. Magari che gira su se stesso, cosi' si capisce meglio.

Il primo esercizio mi sembra facile e lo lascio a qualche altro che si vuole divertire.
Per il secondo, la sommatoria si esprime così:
$S=sum_(k=1)^q(N-4k)^2-sum_(k=1)^q(N-4k)+(N-2)(N-3)+e_n$
dove $q=[N/4]$ [ovvero q è il quoziente intero della divisione di N per 4] ed $e_n$ vale zero se
4 divide N ,1 altrimenti.
Sviluppando i calcoli,salvo possibile errori si trova la...elegantissima formula:
$S=(16)/3q^3+(10-4N)q^2+(N^2-5N+(17)/3)q+(N-2)(N-3)+e_n$
Se mi posso permettere,suggerirei all'amico seascoli di...cambiare argomento !
Per il secondo, la sommatoria si esprime così:
$S=sum_(k=1)^q(N-4k)^2-sum_(k=1)^q(N-4k)+(N-2)(N-3)+e_n$
dove $q=[N/4]$ [ovvero q è il quoziente intero della divisione di N per 4] ed $e_n$ vale zero se
4 divide N ,1 altrimenti.
Sviluppando i calcoli,salvo possibile errori si trova la...elegantissima formula:
$S=(16)/3q^3+(10-4N)q^2+(N^2-5N+(17)/3)q+(N-2)(N-3)+e_n$
Se mi posso permettere,suggerirei all'amico seascoli di...cambiare argomento !
L'hai collaudata questa tua formula?
Mi sa che già per N piccoli sbaglia ...
Ci risentiamo!
Mi sa che già per N piccoli sbaglia ...
Ci risentiamo!
Entrambe le tue formule sono sbagliate.
Nemmeno concordano fra loro! Per N=5 una (la prima) dà 7(esatto) e l'altra 8.
Poi però entrambe sbagliano nel senso che danno risultati troppo grandi.
Per esempio:
N esatto___ sum1__ sum2
5____7______7______8
6___13_____15_____18
9___50_____63_____85
Vedo che ti sei arreso.
Allora te la dò io la fomula, questa sì elegante!
$V_4(N)=1/(4!)[N(N-2)(2N+1)+3(N-:2)]$, dove $(N-:2)$ è il resto della divisione di N per 2.
e coincide con
$\sum_{k=3}^N((k),(3))(-1)^((N-k))$
Nemmeno concordano fra loro! Per N=5 una (la prima) dà 7(esatto) e l'altra 8.
Poi però entrambe sbagliano nel senso che danno risultati troppo grandi.
Per esempio:
N esatto___ sum1__ sum2
5____7______7______8
6___13_____15_____18
9___50_____63_____85
Vedo che ti sei arreso.
Allora te la dò io la fomula, questa sì elegante!
$V_4(N)=1/(4!)[N(N-2)(2N+1)+3(N-:2)]$, dove $(N-:2)$ è il resto della divisione di N per 2.
e coincide con
$\sum_{k=3}^N((k),(3))(-1)^((N-k))$
Il termine "elegantissima" era ironico ( l'ho sottolineato con i puntini sospensivi) proprio perchè non ero sicuro dei miei calcoli.
Mi complimento invece con te per la bella formula.Non l'ho controllata ma sono sicuro che l'hai copiata bene !
Mi complimento invece con te per la bella formula.Non l'ho controllata ma sono sicuro che l'hai copiata bene !
Si, è vero, l'ho copiata! L'ho copiata dal mio quaderno di appunti, quello dedicato ai numeri interi, dove l'avevo annotata la settimana scorsa, quando, nel derivare la somma alternante di coefficienti binomiali del tipo $((k),(3))$, mi sono imbattuto per puro caso nella coincidenza (serendipity?) di avere 2 somme, diversissime di origine, ma che, a parte il segno, davano lo stesso risultato!
Che il tuo termine "elegantissimo" fosse autoironico l'avevo capito benissimo. E che altro poteva essere? Le formule che hai scritto, specie la seconda, sono un esempio gridato di "anti-eleganza", uno schiaffo alla purezza dell'espressione tersa e concisa ... Lo sarebbero state (dico, orribili) anche se fossero state esatte, figuriamoci così. Dico, se uno vuole giocare a barare dando formule sbagliate, sperando che gli altri lascino correre per pigrizia, allora almeno dàlle belle, squisite, tornite, forbite, snelle e leggiadre.
Insomma, diciamo, per usare un eufemismo, che questo tuo penoso tentativo è un capitolo della tua vita su cui conviene abbassare pietosamente un velo. Stammi bene!
Che il tuo termine "elegantissimo" fosse autoironico l'avevo capito benissimo. E che altro poteva essere? Le formule che hai scritto, specie la seconda, sono un esempio gridato di "anti-eleganza", uno schiaffo alla purezza dell'espressione tersa e concisa ... Lo sarebbero state (dico, orribili) anche se fossero state esatte, figuriamoci così. Dico, se uno vuole giocare a barare dando formule sbagliate, sperando che gli altri lascino correre per pigrizia, allora almeno dàlle belle, squisite, tornite, forbite, snelle e leggiadre.
Insomma, diciamo, per usare un eufemismo, che questo tuo penoso tentativo è un capitolo della tua vita su cui conviene abbassare pietosamente un velo. Stammi bene!
Faccio notare a chi legge che la traccia dell'esercizio ,postato lo 02/02,è stata modificata
lo 06/02 ovvero ieri.E per ben due volte !! Il "birichino" seascoli forse non si è accorto
che le modifiche alle tracce vengono inesorabilmente registrate.
Metto tutte e due le mani nel fuoco ed affermo che:
quel f(N-6) che ora si legge nell'ultima stesura del quesito
era in origine un bel f(N-4) !! Cosa che,tra l'altro, rendeva asimmetrica tutta la formula...
La mia risposta è dello 03/02 e quindi di tutt'altro tenore rispetto all'attuale formulazione.
Resterebbe ora da stabilire chi è che imbroglia e poiché io posso aver sbagliato ma non scritto formule a caso....
A parte questo ,voglio rispondere al quesito anche nella sua nuova veste e riportare la seguente formula:
$S=1/3q[16q^2-6(2N-1)q+(3N^2-3N-1)]$ dove è sempre $q=[N/4]$
Anche se non bellissima ( sic !) almeno è farina del mio sacco e non il frutto
di una meccanica,passiva ricopiatura da un quaderno di appunti.
lo 06/02 ovvero ieri.E per ben due volte !! Il "birichino" seascoli forse non si è accorto
che le modifiche alle tracce vengono inesorabilmente registrate.
Metto tutte e due le mani nel fuoco ed affermo che:
quel f(N-6) che ora si legge nell'ultima stesura del quesito
era in origine un bel f(N-4) !! Cosa che,tra l'altro, rendeva asimmetrica tutta la formula...
La mia risposta è dello 03/02 e quindi di tutt'altro tenore rispetto all'attuale formulazione.
Resterebbe ora da stabilire chi è che imbroglia e poiché io posso aver sbagliato ma non scritto formule a caso....
A parte questo ,voglio rispondere al quesito anche nella sua nuova veste e riportare la seguente formula:
$S=1/3q[16q^2-6(2N-1)q+(3N^2-3N-1)]$ dove è sempre $q=[N/4]$
Anche se non bellissima ( sic !) almeno è farina del mio sacco e non il frutto
di una meccanica,passiva ricopiatura da un quaderno di appunti.
Primo. So benissimo che, quando uno modifica il testo di un intervento, la cosa viene registrata (mica sono cieco!)
Secondo. Le mie due modifiche sono state queste:
1) Nel chiedere di calcolare la prima somma avevo scritto, per analogia con la seconda:
Trovare la somma: F(N-1)+F(N-3)+F(N-5)+ etc... con F(x)=x
ma mi è sembrato uno spreco di notazione quello di introdurre una funzione identità per un quesito tutt'altro che difficile.
2) Nella formula che dà la somma dei coefficienti binomiali mi ero accorto di aver omesso un punto esclamativo ed avevo scritto a denominatore 4, invece che 4! = 24.
Queste sono state le mie correzioni.
Terzo. Silvano, dopo avermi offeso insinuando che io abbia "copiato passivamente" la mia formula (che invece mi è costata un'ora di divertente fatica) , ora colma ogni misura, cioè arriva ad insinuare che io abbia messo un testo e, poi, dopo che lui ha fornito la risposta "giusta" , che io l'abbia deliberatamente alterato per coglierlo in errore. Siamo ormai nel dominio della psicopatologia.
Quarto.Tornando alla "copiatura", Silvano sembra così testardamente preso dai suoi deliri da non rendersi conto che il quaderno di appunti di cui parlavo era il "mio" quaderno di appunti, dove trascrivo le "mie" formule, quelle che "io" ho derivato con la "mia" personale fatica. E' chiaro, può darsi che qualcuna delle "mie formule", o forse la maggior parte di esse, siano già note in letteratura, ma non me ne preoccupo: la soddisfazione è averle ricavate da me, con i miei metodi, le mie personali conoscenze, il mio personale intuito e la mia esperienza.
Quinto. A questo punto, ad evitare che il dialogo (se ancora così si può chiamare) degeneri in una schermaglia di insulti gratuiti e vili insinuazioni, quali quelle che ho dovuto subire, chiedo al moderatore di questo "topic" di intevernire per consigliare comportamenti più consoni e, soprattutto, conformi al principio del reciproco rispetto ed alla presunzione di "bona fide" nell'interlocutore.
Secondo. Le mie due modifiche sono state queste:
1) Nel chiedere di calcolare la prima somma avevo scritto, per analogia con la seconda:
Trovare la somma: F(N-1)+F(N-3)+F(N-5)+ etc... con F(x)=x
ma mi è sembrato uno spreco di notazione quello di introdurre una funzione identità per un quesito tutt'altro che difficile.
2) Nella formula che dà la somma dei coefficienti binomiali mi ero accorto di aver omesso un punto esclamativo ed avevo scritto a denominatore 4, invece che 4! = 24.
Queste sono state le mie correzioni.
Terzo. Silvano, dopo avermi offeso insinuando che io abbia "copiato passivamente" la mia formula (che invece mi è costata un'ora di divertente fatica) , ora colma ogni misura, cioè arriva ad insinuare che io abbia messo un testo e, poi, dopo che lui ha fornito la risposta "giusta" , che io l'abbia deliberatamente alterato per coglierlo in errore. Siamo ormai nel dominio della psicopatologia.
Quarto.Tornando alla "copiatura", Silvano sembra così testardamente preso dai suoi deliri da non rendersi conto che il quaderno di appunti di cui parlavo era il "mio" quaderno di appunti, dove trascrivo le "mie" formule, quelle che "io" ho derivato con la "mia" personale fatica. E' chiaro, può darsi che qualcuna delle "mie formule", o forse la maggior parte di esse, siano già note in letteratura, ma non me ne preoccupo: la soddisfazione è averle ricavate da me, con i miei metodi, le mie personali conoscenze, il mio personale intuito e la mia esperienza.
Quinto. A questo punto, ad evitare che il dialogo (se ancora così si può chiamare) degeneri in una schermaglia di insulti gratuiti e vili insinuazioni, quali quelle che ho dovuto subire, chiedo al moderatore di questo "topic" di intevernire per consigliare comportamenti più consoni e, soprattutto, conformi al principio del reciproco rispetto ed alla presunzione di "bona fide" nell'interlocutore.
seascoli mente sapendo di mentire .
f(N-4) è stato sostituito con f(N-6) altrimenti
non avrei commesso gli errori grossolani di cui il "birichino" mi accusa.
Ho rivisto uno per uno i mie fogli di calcolo e su di essi ritrovo ,dal primo
fino all'ultimo ,sempre f(n-4) e non f(N-6) ,furtivamente introdotto
dal "birichino".
Trovo ridicolo l'appello ai moderatori :se questi volessero avere la compiacenza
di confrontare le mie risposte con quelle del "birichino copione " ,troverebbero
una qualche differenza di stile ( e non certo a mio svantaggio).
f(N-4) è stato sostituito con f(N-6) altrimenti
non avrei commesso gli errori grossolani di cui il "birichino" mi accusa.
Ho rivisto uno per uno i mie fogli di calcolo e su di essi ritrovo ,dal primo
fino all'ultimo ,sempre f(n-4) e non f(N-6) ,furtivamente introdotto
dal "birichino".
Trovo ridicolo l'appello ai moderatori :se questi volessero avere la compiacenza
di confrontare le mie risposte con quelle del "birichino copione " ,troverebbero
una qualche differenza di stile ( e non certo a mio svantaggio).
Inguaribile, irrecuperabile! A 71 anni uno ha avuto tutto il tempo per raggiungere un equilibrio interiore.
E invece ...
E invece ...
Altro grossolano errore: quel "38" è la mia età,non la mia data di nascita !!!
Sebbene io sia contrario all'eutanasia comincio a pensare che in certi casi sia proprio necessaria ( leggi seascoli)...
O Jesus!
P.S.
Quest'anno vado per i 39 :spero mi perdonerete la piccola civetteria di quel "38"

Sebbene io sia contrario all'eutanasia comincio a pensare che in certi casi sia proprio necessaria ( leggi seascoli)...
O Jesus!
P.S.
Quest'anno vado per i 39 :spero mi perdonerete la piccola civetteria di quel "38"
Considerazione molto delicata la tua! E' una cosa che sfigurerebbe persino in bocca a un nazista.
Si dà il caso che nella mia famiglia qualcuno ha già subito (a Buchenwald, inverno 1944) il tipo di "eutanasia" che tu non disdegneresti di imporre a chi ha l'unico difetto di non condividere le tue (strampalate) opinioni.
E non aveva ancora compiuto i 38 anni che tu dici ora di avere. Altro che "civetterie"!
Credo sia meglio troncare definitivamente e subito questo scambio ormai sterile e penoso di messaggi.
E' per questo che avevo chiesto l'intervento di un moderatore ...
Si dà il caso che nella mia famiglia qualcuno ha già subito (a Buchenwald, inverno 1944) il tipo di "eutanasia" che tu non disdegneresti di imporre a chi ha l'unico difetto di non condividere le tue (strampalate) opinioni.
E non aveva ancora compiuto i 38 anni che tu dici ora di avere. Altro che "civetterie"!
Credo sia meglio troncare definitivamente e subito questo scambio ormai sterile e penoso di messaggi.
E' per questo che avevo chiesto l'intervento di un moderatore ...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo