Mi serve un ultimo aiuto !!

[Empty Head]

Vi chiedo solo un ultimo aiuto

Ho bisogno di capire come si fanno questi esercizi:

1) Sia f=x^2+1 € Z3[x] , Quali sono gli elementi invertibili in Z3[x]/(f)?

2)Elencare almeno 4 sottoanelli di C

3) Sia a=(2 4) € S5.
Sia H il sottogruppo di S5 i cui elementi sono tutte le permutazioni che lasciano fisso l'elemento 1. Quante permutazioni ci sono nel laterale a*H?

cercate di spiegarmeli con teoria associata ... partendo dalle basi perchè proprio non so come farli
(entro stasera chi può)

grazie ciao

[Sk_Anonymous]

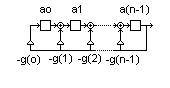
Per quello che riguarda il primo quesito mettiamo in finzione lo shift register qui sopra ponendo p=3 e ‘caricandolo’ con il polinomio generatore g(x)=1+x^2. Gli elementi invertibili in questo caso sono 4 e precisamente…

x^o=1
x^1= x
x^2=2
x^3=2x

La scelta del polinomio generatore non è ottimale in quanto solo la metà dei polinomi di grado 1 in Z|3| diversi dal polinomio nullo [8 polinomi…] viene generato. Scegliendo ad esempio g(x)= 2+x+x^2 tutti e 8 i polinomi diversi da zero risultano invertibili e pertanto formano un campo…

x^o=1
x^1=x
x^2=1+2x
x^3=2+2x
x^4=2
x^5=2x
x^6=2+x
x^7=1+x

cordiali saluti

lupo grigio

[Empty Head]

mai visto quella figura , non penso sia il metodo migliore per spiegarglielo se me lo domanda, non metto in dubbio che sia giusto ma non posso svolgerlo così!

mettetemi un po' di teoria associata a quello che fate , non parlate con un esperto!

grazie

[Sk_Anonymous]

Figura a parte quello che si fà è semplicemente calcolare le potenze di x 'modulo un polinomio g(x)' fino a che non si ottiene, per un certo k, x^k=x^0=1. La sequenza dunque è periodica di periodo k e il polinomi che la formano hanno tutti il polinomio inverso. Per un generico x^i il polinomio inverso è x^(k-i). Nel caso da te proposto g(x)= 1 + x^2 e la sequenza generata ha periodicità 4, ossia è k=4. La massima periodicità ottenibile è p^n-1, dove n è il grado del polinomio generatore g(x). Nel tuo caso è p=3 e n=2, cosicchè la massima periodicità è 8...

Più semplicemente di così non so proprio come spiegarlo...

cordiali saluti

lupo grigio

[Empty Head]

Non ho capito un gran che , ti devo dire la verità , comunque proverò a scervellarmi , grazie.

sapete risolvere anche gli altri?