Inclusione di insiemi

[Sk_Anonymous]

Ciao ragazzi, volevo chiedervi gentilmente se mi date una mano per risolvere la seguente dimostrazione sugli insiemi.

Dimostrare che:

$A \\ (BUC) = (A\\B) nn (A\\C)$

Grazie e ciao !

[Giacballa87]

...mmm dunque è una vita che non traffico più con l'insiemistica...cmq se "\" significa "interseca" allora mi pare abbastanza semplice la faccenda, non è la proprietà distributiva
rispetto all'intersezione e unione? ..sarebbe come dire
A-(B+C)= (A-B)+(A-C)

[Chicco_Stat_1]

\ non significava "meno"?

[Giacballa87]

ah..azz allora per ora non so dire nulla di certo, non ho mai fatto sottrazioni tra insiemi, ma B e C son sottoinsiemi oppure non è detto?...strano dovrei recuperare i libri d mate vecchi

[elgiovo]

?? Che c'è da capire nella sottrazione di insiemi? Se, per esempio $A={1,2,3,4,5}$ e $B={1,4,5}$, $A backslash B={2,3}$. Comunque basta guardare quest'immagine per capire che la proposizione è vera. In ambedue i casi il risultato è l'area tratteggiata.

[Sk_Anonymous]

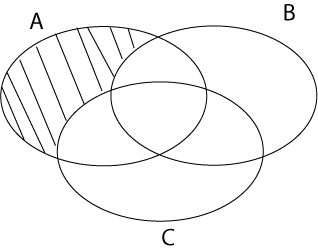
Grazie, ma in particolare mi interessava la dimostrazione scritta e formale delle due inclusioni (da sx a dx e viceversa). Grazie cmq per il diagramma di Eulero-Venn.
Giampaolo

[giuseppe87x]

La devi dimostrare come uguaglianza insiemistica; in particolare devi far vedere che se un elemento appartiene al primo membro, deve appartenere anche al secondo e viceversa.

[amel3]

La dimostrazione e quasi tautologica...

$x in A \\ (B\ U\ C) <=> { (x in A), (x notin B\ U\ C):} <=> \ {(x in A), (x notin B \ e\ x notin C):} <=> {( x in A \ e\ x notin B\), (x in A \ e\ x notin C):} <=>{( x in A\\B), (x in A\\C):} <=> x in A\\B\ nn\ B\\C$

Sarò riuscito a sbagliare qualcosa persino qui? A quel punto merito un premio...

[Giacballa87]

...chieddo umilmente scusa...mi son guardato la sottrazione tra insiemi ( ringrazio gli insegnanti ke ho avuto fin'ora per avermi rotto le palle cn l'insiemisica e poi nn farmi fare una banale sottrazione...!)
Son dell'idea di amel: la dimostrazione è quasi tautologica, anche se quel che ha scritto dopo lo è un po' meno.