Implicazioni logiche e dubbi sconcertanti!
Salve ragazzi, sono qui per porvi un quesito che mi ha spiazzato nonostante sia di una banalità estrema ed anche - al termine del post - una curiosità sull'utilizzo delle implicazioni logiche da parte dei docenti universitari:
In pratica la tavola della verità per l'implicazione logica è la seguente:
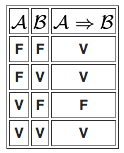
Fondamentalmente mi è tutto chiaro, ad eccezione di questo caso, leggete con attenzione:
Se 10 è un numero dispari, allora 10 è divisibile per 2.
Le due proposizioni sono:
\(\displaystyle A \) = 10 è un numero dispari (FALSA)
\(\displaystyle B \) = 10 è divisibile per 2 (VERA)
In base alla tabella di cui sopra, l'implicazione \(\displaystyle A\Rightarrow B \) dovrebbe essere VERA, ma sinceramente mi sfugge il senso...A me sembra una frase obiettivamente falsa, sbaglio?
Il secondo dubbio che poco c'entra con il primo, ma riguarda sempre l'implicazione logica è:
perché i docenti universitari (ingegneria) nelle dimostrazioni utilizzano sempre l'implicazione logica nel corso dei passasggi algebrici. Un esempio banale:
\(\displaystyle a+2a+b=c \Rightarrow 3a+b=c \)
Cioè è formalmente (totalmente) scorretto scrivere così? Non si dovrebbe usare l'equivalenza logica (\(\displaystyle \Leftrightarrow \))? Oppure anche una scrittura del genere è corretta? perché altrimenti andrebbe obiettato alla stragrande maggioranza dei miei prof!
Grazie mille! Spero in una celere e chiara risposta!
In pratica la tavola della verità per l'implicazione logica è la seguente:
Fondamentalmente mi è tutto chiaro, ad eccezione di questo caso, leggete con attenzione:
Se 10 è un numero dispari, allora 10 è divisibile per 2.
Le due proposizioni sono:
\(\displaystyle A \) = 10 è un numero dispari (FALSA)
\(\displaystyle B \) = 10 è divisibile per 2 (VERA)
In base alla tabella di cui sopra, l'implicazione \(\displaystyle A\Rightarrow B \) dovrebbe essere VERA, ma sinceramente mi sfugge il senso...A me sembra una frase obiettivamente falsa, sbaglio?
Il secondo dubbio che poco c'entra con il primo, ma riguarda sempre l'implicazione logica è:
perché i docenti universitari (ingegneria) nelle dimostrazioni utilizzano sempre l'implicazione logica nel corso dei passasggi algebrici. Un esempio banale:
\(\displaystyle a+2a+b=c \Rightarrow 3a+b=c \)
Cioè è formalmente (totalmente) scorretto scrivere così? Non si dovrebbe usare l'equivalenza logica (\(\displaystyle \Leftrightarrow \))? Oppure anche una scrittura del genere è corretta? perché altrimenti andrebbe obiettato alla stragrande maggioranza dei miei prof!
Grazie mille! Spero in una celere e chiara risposta!
Risposte
1: Cosa significa "obiettivamente falsa" ?
2: usano l'implicazione, potrebbero usare la doppia implicazione. Ma francamente non credo sia un errore, semplicemente stanno facendo un passaggio e usano la freccia per far capire meglio.
2: usano l'implicazione, potrebbero usare la doppia implicazione. Ma francamente non credo sia un errore, semplicemente stanno facendo un passaggio e usano la freccia per far capire meglio.
"FE":
1: Cosa significa "obiettivamente falsa" ?
Significa che se io mi rivolgo a qualcuno dicendo: "Se 10 è un numero dispari allora 10 è divisibile per 2" non mi pare sia un'affermazione VERA, come invece indica la tabella dellle verità!. Sbaglio?
Stai facendo confusione con l'esempio.
Dire " 10 non è un numero dispari o 10 è divisibile per 2" ti sembra più sensatamente vera? Nota che è vera se almeno una delle due è vera, e in questo caso sono entrambe vere.
Dire " 10 non è un numero dispari o 10 è divisibile per 2" ti sembra più sensatamente vera? Nota che è vera se almeno una delle due è vera, e in questo caso sono entrambe vere.
FE ma se poni attenzione alla tabella essa dice: Se la proposizione A è FALSA e la proposizione B è VERA, allora \(\displaystyle A \Rightarrow B\) è VERA (2° riga della tabella).
Quindi il mio esempio è corretto.
Se 10 è un numero dispari (FALSA), allora 10 è divisibile per 2 (VERA).
ll tuo esempio è completamente diverso perché tu poni come prima proposizione una proposizione VERA (10 NON è un numero dispari), io invece ho volutamente posto una proposizione falsa, per rientrare nel caso 2 della tabella di sopra.
EDIT: In realtà, dopo aver fatto svariate ricerche, credo innanzitutto che quella su cui stiamo discutendo non sia un'implicazione logica, ma bensì un'implicazione materiale che in effetti ho letto avere queste "problematiche". Quindi questo mi fa dedurre che Wikipedia, riportando sotto la voce di implicazione logica, la tabella delle verità, commetta un errore.
Il simbolo \(\displaystyle \Rightarrow \) che noi usiamo nelle dimostrazioni non ha nulla a che fare con quella tabella delle verità e bensì serve ad esprimere che: se è vero questo (ipotesi)...allora è vero quest'altro (tesi), cioè è "figlio" dell'implicazione materiale (come si può ben immaginare), ma non è la stessa cosa.
Quindi il mio esempio è corretto.
Se 10 è un numero dispari (FALSA), allora 10 è divisibile per 2 (VERA).
ll tuo esempio è completamente diverso perché tu poni come prima proposizione una proposizione VERA (10 NON è un numero dispari), io invece ho volutamente posto una proposizione falsa, per rientrare nel caso 2 della tabella di sopra.
EDIT: In realtà, dopo aver fatto svariate ricerche, credo innanzitutto che quella su cui stiamo discutendo non sia un'implicazione logica, ma bensì un'implicazione materiale che in effetti ho letto avere queste "problematiche". Quindi questo mi fa dedurre che Wikipedia, riportando sotto la voce di implicazione logica, la tabella delle verità, commetta un errore.
Il simbolo \(\displaystyle \Rightarrow \) che noi usiamo nelle dimostrazioni non ha nulla a che fare con quella tabella delle verità e bensì serve ad esprimere che: se è vero questo (ipotesi)...allora è vero quest'altro (tesi), cioè è "figlio" dell'implicazione materiale (come si può ben immaginare), ma non è la stessa cosa.
Io ho semplicemente riformulato la tua frase.
Dire $ p rArr q $ è esattamente come dire $ neg p vv q $ .
Dire $ p rArr q $ è esattamente come dire $ neg p vv q $ .
Cioè secondo te dire 10 è un numero dispari, allora 10 è divisibile per 2 ha lo stesso significato di 10 NON è un numero dispari, allora 10 è divisibile per 2?
Cioè non è sconcertante? (non me la prendo con te, ma con la forumalazione matematica che mi sconcerta!!!)
Secondo me sono due formulazioni completamente diverse..
Cioè non è sconcertante? (non me la prendo con te, ma con la forumalazione matematica che mi sconcerta!!!)
Secondo me sono due formulazioni completamente diverse..
leggi meglio quello che ho scritto
Dire p⇒q è esattamente come dire ¬p∨q
comunque è normale fare confusione e rimanere sconcertati dalla tabella di verità delle formule logiche se si inizia a farsi esempi mentali con frasi comuni come i tuoi è facile cadere in confusione
Ah ok! Allora chiedo scusa!! Ora ho capito.
Immagino che questa uguaglianza $ p rArr q $ esattamente come dire $ neg p vv q $ derivi da una dimostrazione che giustifica il secondo caso della tabella! Dico bene?
Sei d'accordo con me quando dicevo che implicazione materiale e implicazione logica sono cose diverse? e nelle dimostrazioni noi usiamo la implicazione logica (ipotesi (vera)$ rArr $ tesi), quindi non avremo mai il caso 2 della tabella.
Cioè le cosidette "seghe"
mentali sono solo appannaggio dell'implicazione materiale.
Infine, il fatto di usare l'implicazione logica al posto dell'equivalenza, hai già detto che secondo te è giusto, ma matematicamente non è un errore?
Ora ho capito. Immagino che questa uguaglianza $ p rArr q $ esattamente come dire $ neg p vv q $ derivi da una dimostrazione che giustifica il secondo caso della tabella! Dico bene?
Sei d'accordo con me quando dicevo che implicazione materiale e implicazione logica sono cose diverse? e nelle dimostrazioni noi usiamo la implicazione logica (ipotesi (vera)$ rArr $ tesi), quindi non avremo mai il caso 2 della tabella.
Cioè le cosidette "seghe"
mentali sono solo appannaggio dell'implicazione materiale. Infine, il fatto di usare l'implicazione logica al posto dell'equivalenza, hai già detto che secondo te è giusto, ma matematicamente non è un errore?
Le due espressioni hanno la stessa tavola di verità, quindi sono logicamente equivalenti. Non ha a che fare nello specifico con il secondo caso.
Su ciò che dici di implicazione logica e materiale non so nulla, mi dispiace.
Comunque fai attenzione: quando fai una dimostrazione vuoi dimostrare la verità di una tesi. La tabella di verità ti dice solo che l'implicazione è vera, ma i valori di verità dell'ipotesi e della tesi li conosci già.
Per quanto riguarda i passaggi algebrici, non è un errore perché stai semplicemente facendo dei passaggi algebrici, la freccia è un " quindi " ma io non ci mischierei la logica perché è inutile e fai soltanto confusione. Se scrivo 2+2=4 allora 4-2=2 non è che c'è bisogno di dire "e viceversa" .
Su ciò che dici di implicazione logica e materiale non so nulla, mi dispiace.
Comunque fai attenzione: quando fai una dimostrazione vuoi dimostrare la verità di una tesi. La tabella di verità ti dice solo che l'implicazione è vera, ma i valori di verità dell'ipotesi e della tesi li conosci già.
Per quanto riguarda i passaggi algebrici, non è un errore perché stai semplicemente facendo dei passaggi algebrici, la freccia è un " quindi " ma io non ci mischierei la logica perché è inutile e fai soltanto confusione. Se scrivo 2+2=4 allora 4-2=2 non è che c'è bisogno di dire "e viceversa" .
Ah, l'implicazione logica...
Sì, sbagli. E' 'l'intera frase ad essere vera. Ti faccio un controesempio:
"Se 10 è un numero dispari, allora 10 è divisibile per 7." E' vera o falsa secondo te?
Te la faccio più semplice e ti spiego perché sei stato sviato: nel linguaggio corrente siamo interessati alla verità della proposizione solo se la premessa è vera, visto che da una falsa può seguire qualunque cosa. Quindi quando facciamo esempi con la premessa falsa all'inizio rimaniamo sconcertati.
Per approfondire suggerisco anche questa interessante discussione sul Teorema Universale.
"Mathcrazy":
Fondamentalmente mi è tutto chiaro, ad eccezione di questo caso, leggete con attenzione:
Se 10 è un numero dispari, allora 10 è divisibile per 2.
Le due proposizioni sono:
\(\displaystyle A \) = 10 è un numero dispari (FALSA)
\(\displaystyle B \) = 10 è divisibile per 2 (VERA)
In base alla tabella di cui sopra, l'implicazione \(\displaystyle A\Rightarrow B \) dovrebbe essere VERA, ma sinceramente mi sfugge il senso...A me sembra una frase obiettivamente falsa, sbaglio?
Sì, sbagli. E' 'l'intera frase ad essere vera. Ti faccio un controesempio:
"Se 10 è un numero dispari, allora 10 è divisibile per 7." E' vera o falsa secondo te?
Te la faccio più semplice e ti spiego perché sei stato sviato: nel linguaggio corrente siamo interessati alla verità della proposizione solo se la premessa è vera, visto che da una falsa può seguire qualunque cosa. Quindi quando facciamo esempi con la premessa falsa all'inizio rimaniamo sconcertati.
Per approfondire suggerisco anche questa interessante discussione sul Teorema Universale.
Per spiegare ancora meglio la confusione che fai tra verità di un'implicazione e verità di una tesi che vuoi dimostrare ti cito DeMarco, Analisi Uno, che riporta a sua volta un aneddoto molto famoso:
Si racconta che a una conferenza Bertrand Russell avesse illustrato il fatto (ex falso quodlibet sequitur) sopra esposto. Uno degli ascoltatori lo sfidò: " Non ci credo! Mi dimostri che se 3=4, allora lei è il Papa." Russell non era ovviamente tenuto a dimostrare di essere il papa, visto che 3 è diverso da 4, e dunque l'implicazione è vera indipendentemente dalla verità o meno della tesi. In questo modo Russell raccolse la sfida: da 3=4 sottraendo 2 a entrambi i membri si ha 1=2; lei presume che io e il papa siamo due persone diverse, ma 1=2, quindi io sono il Papa!
Confermo anche io avevo stessi dubbi, non bisogna confondere la implicazione materiale con la implicazione logica.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo