Filtraggio inverso...
Ragazzi
vedo con piacere che avete subito dimostrato interesse per la crittografia e ciò è buona cosa. E’ opportuno però ricordare che questo spazio è dedicato in generale alla Matematica discreta e non solamente alla crittografia. Così ho pensato bene di inaugurarlo con un quesito che con la crittografia non ha nulla a che fare ma che rientra nel tema generale…
Supponiamo di avere lo schema seguente…
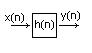
La black box sia un sistema tempo-discreto lineare invariante e casuale caratterizzato da una risposta impulsiva $h(n)$. In tal caso la relazione ingresso uscita è data da…
$y(n)= sum_(i=0)^(+oo) h_i*x(n-i)$ (1)
Supponiamo di conoscere $h(n)$ e $y(n)$, di non conoscere l’ingresso $ x(n)$ e volerlo valutare. Un problema del genere è chiamato in letteratura filtraggio inverso. Due quesiti assai semplici:
a) è sempre possibile date $y(n)$ e $h(n)$ trovare la $x(n)$?…
b) nei casi in cui è possibile come si procede?…
cordiali saluti
lupo grigio

an old wolf may lose his teeth, but never his nature
vedo con piacere che avete subito dimostrato interesse per la crittografia e ciò è buona cosa. E’ opportuno però ricordare che questo spazio è dedicato in generale alla Matematica discreta e non solamente alla crittografia. Così ho pensato bene di inaugurarlo con un quesito che con la crittografia non ha nulla a che fare ma che rientra nel tema generale…
Supponiamo di avere lo schema seguente…
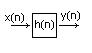
La black box sia un sistema tempo-discreto lineare invariante e casuale caratterizzato da una risposta impulsiva $h(n)$. In tal caso la relazione ingresso uscita è data da…
$y(n)= sum_(i=0)^(+oo) h_i*x(n-i)$ (1)
Supponiamo di conoscere $h(n)$ e $y(n)$, di non conoscere l’ingresso $ x(n)$ e volerlo valutare. Un problema del genere è chiamato in letteratura filtraggio inverso. Due quesiti assai semplici:
a) è sempre possibile date $y(n)$ e $h(n)$ trovare la $x(n)$?…
b) nei casi in cui è possibile come si procede?…
cordiali saluti
lupo grigio

an old wolf may lose his teeth, but never his nature
Risposte
Non vorrei aver frainteso (ma mi sa di sì, perché non conosco questi argomenti), ma a me sa tanto di formula di inversione di Moebius (la terza, per essere precisi).
Cioè, ponendo $f(i*n)=h_ix(n-i)$, si ha $y(n)=\sum_{i=0}^(+oo)f(i*n)$. E la $f(n)$ si ricava dalla formula di inversione $f(n)=\sum_{i=1}^(+oo)\mu(n)y(nx)$, sempre se $\sum_{m,n}|f(mnx)|$ converge.. Solo che la terza formula di inversione vale a partire da $i=1$, quindi può essere che mi sbagli.
Cioè, ponendo $f(i*n)=h_ix(n-i)$, si ha $y(n)=\sum_{i=0}^(+oo)f(i*n)$. E la $f(n)$ si ricava dalla formula di inversione $f(n)=\sum_{i=1}^(+oo)\mu(n)y(nx)$, sempre se $\sum_{m,n}|f(mnx)|$ converge.. Solo che la terza formula di inversione vale a partire da $i=1$, quindi può essere che mi sbagli.
Diciamo che una strada abbastanza ‘diretta’ [che può essere anche la citata ‘formula di Moebius’…] consiste in questo. Dato che è…
$y(n)= sum_(i=0)^(+oo) h_i*x(n-i)$ (1)
… se per ipotesi è $h_0ne0$ si può procedere così…
$y(0)=h_0*x(0)$ -> $x(0)=(y(0))/h_0$
$y(1)=h_0*x(1)+h_1*x(0)$ -> $x(1) = (y(1)-h_1*x(0))/h_0$
…
$y(k)= sum_(i=0)^k h_i*x(k-i)$ -> $x(k)=1/h_0*(y(k)-sum_(i=1)^k h_i*x(k-i))$ (2)
E’ così?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
$y(n)= sum_(i=0)^(+oo) h_i*x(n-i)$ (1)
… se per ipotesi è $h_0ne0$ si può procedere così…
$y(0)=h_0*x(0)$ -> $x(0)=(y(0))/h_0$
$y(1)=h_0*x(1)+h_1*x(0)$ -> $x(1) = (y(1)-h_1*x(0))/h_0$
…
$y(k)= sum_(i=0)^k h_i*x(k-i)$ -> $x(k)=1/h_0*(y(k)-sum_(i=1)^k h_i*x(k-i))$ (2)
E’ così?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
"lupo grigio":
... lineare invariante e casuale caratterizzato ...
causale?
Diciamo che una strada
…
$y(k)= sum_(i=0)^k h_i*x(k-i)$ -> $x(k)=1/h_0*(y(k)-sum_(i=1)^k h_i*x(k-i))$ (2)
E’ così?…
sì, diciamo che grazie alla causalità dobbiamo risolvere un sistema triangolare.
Mi fa piacere aver ricevuto l’avvallo al mio 'calcolo', per la verità alquanto semplice. Operando in questo modo vi è però un problema. Supponiamo che il sistema lineare invariante e causale [  …] abbia una risposta all’impulso finita [ossia un FIR…], diciamo di lunghezza $N$. In tal caso per $k>N-1$ la formula diviene…
…] abbia una risposta all’impulso finita [ossia un FIR…], diciamo di lunghezza $N$. In tal caso per $k>N-1$ la formula diviene…
$x(k)= 1/h_0*(y(k) – sum_(i=1)^(N-1) h_i*x(k-i))$ (1)
In termini di z-trasformata la (1) si scrive…
$X(z)= 1/h_0* (Y(z))/(D(z))$ (2)
... con…
$D(z)= 1+sum_(i=1)^(N-1) h_i/h_0*z^(-i)$ (3)
Ora perché la risposta non diverga è necessario che il polinomio $D(z)$ abbia radici tutte all’interno del cerchio unitario. Questo è garantito in ogni caso?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
 …] abbia una risposta all’impulso finita [ossia un FIR…], diciamo di lunghezza $N$. In tal caso per $k>N-1$ la formula diviene…
…] abbia una risposta all’impulso finita [ossia un FIR…], diciamo di lunghezza $N$. In tal caso per $k>N-1$ la formula diviene… $x(k)= 1/h_0*(y(k) – sum_(i=1)^(N-1) h_i*x(k-i))$ (1)
In termini di z-trasformata la (1) si scrive…
$X(z)= 1/h_0* (Y(z))/(D(z))$ (2)
... con…
$D(z)= 1+sum_(i=1)^(N-1) h_i/h_0*z^(-i)$ (3)
Ora perché la risposta non diverga è necessario che il polinomio $D(z)$ abbia radici tutte all’interno del cerchio unitario. Questo è garantito in ogni caso?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
è garantito se H(z) è a fase minima (a meno di errori da parte mia)
Certo... ma in tal caso alle ipotesi fatte in precedenza occorre aggiungere la condizione che $H(z)$ sia a 'fase minima'... e se non è così che si fà?... 

cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Siamo passati da $Y(z)=H(z)X(z)$ a $X(z)=H^(-1)(z)Y(z)$. Poli e zeri si scambiano passando da $H$ a $H^(-1)$ (in questo caso H è soli zeri essendo FIR), e se H non è a fase minima, $H^(-1)$ è instabile.
Una delle applicazioni che ha mostrato la grande potenza degli algoritmi di signal processing è legata al mondo della musica. Tutti sappiamo che un brano musicale registrato in una ambiente soggetto a ‘riverberi’ [tipicamente una chiesa o un teatro non progettato in maniera ‘idonea’ allo scopo…] è in alcuni casi assai ‘sgradevole’ da sentire. In particolare in certe posizioni certe ‘note’ risultano praticamente non udibili in quanto il ‘segnale principale’ e i riverberi si sommano in opposizione di fase autocancellandosi. Una maniera intelligente di porre rimedio a questo consiste nel costruire un ‘modello’ dell’ambiente in cui il brano musicale è stato registrato secondo lo schema già visto…
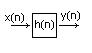
Qui $x(n)$ rappresenta il brano musicale ‘incorrotto’, $y(n)$ il brano musicale soggetto ai riverberi e $h(n)$ la ‘risposta all’impulso’ dell’ambiente di registrazione. Passando alle traformate se $H(z)$ è invertibile sarà…
$X(z)= Y(z)*H^(-1)(z)$ (1)
… e il gioco è fatto. In altre parole se si conosce $h(n)$ e si ha la registrazione $y(n)$, $x(n)$ può essere ottenuta dalla convoluzione di $y(n)$ con la ‘sequenza inversa’ di $h(n)$. Negli anni ’70 ha destato un certo ‘scalpore’ la ‘riedizione’ di alcune incisioni discografiche di Caruso registrate in analogico negli anni ’20 e ‘riproposte’ cinquant’anni dopo debitamente ‘ripulite’. Da allora è divenuta pratica ‘standard’ quella di caratterizzare la ‘firma’ $h(n)$ di un ambiente registrazione allo scopo di applicare sempre tale tecnica…
Come abbiamo visto condizione necessaria perché $h(n)$ sia ‘invertibile’ è che sia a fase minima. Che significa?… Significa che se scriviamo…
$H(z)= h_0*(N(z))/(D(z))$ (2)
... il polinomio $N(z)$ deve avere tutte le radici in modulo minori di 1, ossia stare [sul piano delle $z$…] entro il cerchio con centro l’origine e raggio uguale ad 1. In tal caso è assicurato che il ‘filtro inverso’…
$H^(-1) (z)= 1/h_0 * (D(z))/(N(z))$ (3)
... è stabile. Facciamo un paio di esempi. Supponiamo da prima che la nostra ‘stanza’ abbia risposta…
$y(n)= x(n)+1/2*x(n-4)$ (4)
… cui corrisponde…
$H_1(z)= 1+1/2*z^(-4)$ (5)
Supponiamo poi che un’altra ‘stanza’ abbia risposta…
$y(n)=x(n)+2*x(n-4)$ (6)
… cui corriponde…
$H_2(z)=1+2*z^(-4)$ (7)
Nella figura che segue…
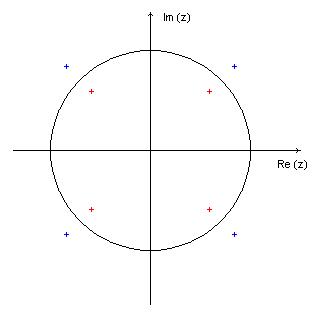
… sono riportate in rosso le radici di $H_1$ e in azzurro le radici di $H_2$. Per quanto detto prima $H_1$ è ‘invertibile’ mentre $H_2$ non lo è. La domanda ora è questa: se la stanza di registrazione è caratterizzata da una risposta simile ad $H_2$ dobbiamo ‘rassegnarci’ ad ascoltare musica ‘cattiva’ o possiamo tentare di fare qualche cosa?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Qui $x(n)$ rappresenta il brano musicale ‘incorrotto’, $y(n)$ il brano musicale soggetto ai riverberi e $h(n)$ la ‘risposta all’impulso’ dell’ambiente di registrazione. Passando alle traformate se $H(z)$ è invertibile sarà…
$X(z)= Y(z)*H^(-1)(z)$ (1)
… e il gioco è fatto. In altre parole se si conosce $h(n)$ e si ha la registrazione $y(n)$, $x(n)$ può essere ottenuta dalla convoluzione di $y(n)$ con la ‘sequenza inversa’ di $h(n)$. Negli anni ’70 ha destato un certo ‘scalpore’ la ‘riedizione’ di alcune incisioni discografiche di Caruso registrate in analogico negli anni ’20 e ‘riproposte’ cinquant’anni dopo debitamente ‘ripulite’. Da allora è divenuta pratica ‘standard’ quella di caratterizzare la ‘firma’ $h(n)$ di un ambiente registrazione allo scopo di applicare sempre tale tecnica…
Come abbiamo visto condizione necessaria perché $h(n)$ sia ‘invertibile’ è che sia a fase minima. Che significa?… Significa che se scriviamo…
$H(z)= h_0*(N(z))/(D(z))$ (2)
... il polinomio $N(z)$ deve avere tutte le radici in modulo minori di 1, ossia stare [sul piano delle $z$…] entro il cerchio con centro l’origine e raggio uguale ad 1. In tal caso è assicurato che il ‘filtro inverso’…
$H^(-1) (z)= 1/h_0 * (D(z))/(N(z))$ (3)
... è stabile. Facciamo un paio di esempi. Supponiamo da prima che la nostra ‘stanza’ abbia risposta…
$y(n)= x(n)+1/2*x(n-4)$ (4)
… cui corrisponde…
$H_1(z)= 1+1/2*z^(-4)$ (5)
Supponiamo poi che un’altra ‘stanza’ abbia risposta…
$y(n)=x(n)+2*x(n-4)$ (6)
… cui corriponde…
$H_2(z)=1+2*z^(-4)$ (7)
Nella figura che segue…

… sono riportate in rosso le radici di $H_1$ e in azzurro le radici di $H_2$. Per quanto detto prima $H_1$ è ‘invertibile’ mentre $H_2$ non lo è. La domanda ora è questa: se la stanza di registrazione è caratterizzata da una risposta simile ad $H_2$ dobbiamo ‘rassegnarci’ ad ascoltare musica ‘cattiva’ o possiamo tentare di fare qualche cosa?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
si potrebbe dare in pasto a $H_2^(-1)$ la sequenza ${y_(-n)}$ invece che ${y_n}$, rinunciando così a sistemi in tempo reale (a patto di introdurre un ritardo dovuto alla memorizzazione di ${y_n}$)
Uhmmmm!… veramente mi pare che se $H_2^(-1)(z)$ è instabile qualsiasi cosa le ‘diamo in pasto’ saranno problemi… o no?… Vediamo allora di impostare un poco il problema in termini più 'appropriati'…
Supponiamo per il momento che il ‘filtro diretto’ abbia una risposta all’impulso di lunghezza finita. Diciamo allora che una sequenza qualsiasi lunga $n$ può essere rappresentata in forma di z-trasformata come…
$P(z)= c_0+c_1*z^(-1)+c_2*z^(-2)... +c_(n-2)*z^(-n+2)+c_(n-1)*z^(-n+1)=$
$= c_0*(1-r_1*z^(-1))*(1-r_2*z^(-1))… (1-r_(n-2)*z^(-1))*(1-r_(n-1)*z^(-1))$ (1)
... essendo le $r_i$, $ i=1,2,...,n-1$ le radici del polinomio in $z^(-1)$ di grado $n-1$.
Data $P(z)$ è possibile definire la sequenza inversa $Q(z)$ come…
$Q(z)=c_0*z^(-n+1)+c_1*z^(-n+2)+...+c_(n-2)*z^(-1)+c_(n-1)=$
$= c_0*z^(-n+1)*(1-r_1*z)*(1-r_2*z)*...*(1-r_(n-2)*z)*(1-r_(n-1)*z)$ (2)
Dal confronto tra la (1) e la (2) è abbastanza immediato verificare che se $alpha$ è radice di $P$, allora $1/alpha$ è radice di $Q$. Questo significa che per $Q$ vale lo sviluppo…
$Q(z)= Inv [P(z)]= c_(n-1) * (1-z^(-1)/(r_1))*(1-z^(-1)/(r_2))*...*(1-z^(-1)/(r_(n-2)))*(1-z^(-1)/(r_(n-1)))$ (3)
… ove con $Inv$ abbiamo indicato un operatore che associa ad una sequenza la sua inversa…
Definiamo ora il concetto di ‘sequenza a fase minima’ e ‘sequenza a fase massima’. Una sequenza $P(z)$ si dice a fase minima se tutte le sue radici sono in modulo minori [o uguali] a 1. Una sequenza $Q(z)$ si dice a fase massima se tutte le sue radici sono in modulo maggiori [o uguali] a 1. Và da sé che per una qualunque sequenza $H(z)$ è…
$H(z)$ = $H_p(z)*H_q(z)$ (4)
… dove $H_p$ è a fase minima e $H_q$ è a fase massima. Va pure da sé che la convoluzione di due sequenza a fase minima è a fase minima e la convoluzione di due sequenza a fase massima è a fase massima…
Và bene quello che ho scritto fin qui?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Supponiamo per il momento che il ‘filtro diretto’ abbia una risposta all’impulso di lunghezza finita. Diciamo allora che una sequenza qualsiasi lunga $n$ può essere rappresentata in forma di z-trasformata come…
$P(z)= c_0+c_1*z^(-1)+c_2*z^(-2)... +c_(n-2)*z^(-n+2)+c_(n-1)*z^(-n+1)=$
$= c_0*(1-r_1*z^(-1))*(1-r_2*z^(-1))… (1-r_(n-2)*z^(-1))*(1-r_(n-1)*z^(-1))$ (1)
... essendo le $r_i$, $ i=1,2,...,n-1$ le radici del polinomio in $z^(-1)$ di grado $n-1$.
Data $P(z)$ è possibile definire la sequenza inversa $Q(z)$ come…
$Q(z)=c_0*z^(-n+1)+c_1*z^(-n+2)+...+c_(n-2)*z^(-1)+c_(n-1)=$
$= c_0*z^(-n+1)*(1-r_1*z)*(1-r_2*z)*...*(1-r_(n-2)*z)*(1-r_(n-1)*z)$ (2)
Dal confronto tra la (1) e la (2) è abbastanza immediato verificare che se $alpha$ è radice di $P$, allora $1/alpha$ è radice di $Q$. Questo significa che per $Q$ vale lo sviluppo…
$Q(z)= Inv [P(z)]= c_(n-1) * (1-z^(-1)/(r_1))*(1-z^(-1)/(r_2))*...*(1-z^(-1)/(r_(n-2)))*(1-z^(-1)/(r_(n-1)))$ (3)
… ove con $Inv
Definiamo ora il concetto di ‘sequenza a fase minima’ e ‘sequenza a fase massima’. Una sequenza $P(z)$ si dice a fase minima se tutte le sue radici sono in modulo minori [o uguali] a 1. Una sequenza $Q(z)$ si dice a fase massima se tutte le sue radici sono in modulo maggiori [o uguali] a 1. Và da sé che per una qualunque sequenza $H(z)$ è…
$H(z)$ = $H_p(z)*H_q(z)$ (4)
… dove $H_p$ è a fase minima e $H_q$ è a fase massima. Va pure da sé che la convoluzione di due sequenza a fase minima è a fase minima e la convoluzione di due sequenza a fase massima è a fase massima…
Và bene quello che ho scritto fin qui?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
"luca.barletta":
si potrebbe dare in pasto a $H_2^(-1)$ la sequenza ${y_(-n)}$ invece che ${y_n}$, rinunciando così a sistemi in tempo reale (a patto di introdurre un ritardo dovuto alla memorizzazione di ${y_n}$)
l'idea c'è ma non sono stato molto preciso; rimedio ora:
stiamo considerando il sistema $X(z)=Y(z)(N(z))/(D(z))$ (usando la tua notazione); potremmo portare a termine la deconvoluzione suddividendo la parte causale da quella anticausale del sistema:
$X(z)=Y(z)(N(z))/(D_(min)(z))*1/(D_(max)(z))$
dove in $D_(min)(z)$ ho raggruppato tutte le radici entro il cerchio unitario (poli a fase minima), e in $D_(max)(z)$ le radici fuori dal cerchio (poli a fase massima).
Ora, possiamo convolvere ${y_n}$ con la parte causale-convergente del sistema, cioè $(N(z))/(D_(min)(z))$, ottenendo il risultato intermedio:
$X^{\prime}(z)=Y(z)(N(z))/(D_(min)(z))$
che è la zeta-trasformata della sequenza ${x_n^{\prime}}$; quest'ultima deve essere convoluta con la parte rimanente del sistema, che è causale-instabile ovvero anticausale-stabile.
Per fare ciò è sufficiente ribaltare l'asse temporale, infatti ${x_(-n)^{\prime}}harrX^{\prime}(1/z)$ e dunque:
$X(1/z)=(X^{\prime}(1/z))/(D_(max)(1/z))$
dove $D_(max)(1/z)$ ha le radici reciproche di $D_(max)(z)$ e quindi all'interno del cerchio unitario.
Infine la sequenza corrispondente a $X(1/z)$ deve ancora essere ribaltata nel tempo per ottenere ${x_n}$
Diciamo che certamante 'l’idea c’è' anche se preferisco, come sempre, andare avanti con i cosiddetti ‘piedi di piombo’…
Intanto vale sempre l’ipotesi che il filtro che si deve ‘invertire’ abbia risposta all’impulso finita. Nello scorso postato abbiamo visto che per una qualunque z-trasformata $H(z)$ di soli zeri possiamo scrivere…
$H(z)=H_p(z)*H_q(z)$ (1)
… ove con $H_p$ e $H_q$ si intendono le componenti di $H$ rispettivamente ‘a fase minima’ e ‘a fase massima’. Di conseguenza la relazione ingresso/uscita del sistema seguente…
… potrà essere scritta come…
$Y=Y_p*Y_q= H_p*H_q*X_p*X_q$ (2)
… dove è evidente che è…
$Y_p=H_p*X_p$, $Y_q=H_q*X_q$ (3)
Le semplici equazioni (3) sono assai utili perchè dimostrano che le componenti a fase minima e fase massima di $Y$ possono essere trattate separatamente. Dal momento che sappiamo che una funzione FIR a fase minima è invertibile possiamo senz’altro scrivere…
$X_p=H_p^(-1)*Y_p$ (4)
Per quanto riguarda le componenti a fase massima invece occorre prendere una strada differente. Dal momento che una sequenza a fase massima può essere trasformata a fase minima con l’operazione di inversione possiamo scrivere…
$Inv[Y_q]= Inv[H_q]*Inv[X_q]$ (5)
… da cui con un poco si passaggi si ottiene…
$X_q= Inv[Inv^(-1)[H_q]*Inv[Y_q]]$ (6)
Una volta note $X_p$ e $X_q$ è immediato trovare…
$X(z)=X_p(z)*X_q(z)$ (7)
La procedura per realizzare il filtro inverso di una $H(z)$ qualunque può essere dunque ipotizzato nel seguente modo…
a) si scompongono in fattori le due sequenze $H(z)$ e $Y(z)$
b) si separano le componenti a fase minima e massima di $H(z)$ e $Y(z)$
c) si calcola $X_p$ con la (4)
d) si calcola $X_q$ con la (5)
e) si calcola $X$ con la (7)
Il metodo è certo attraente per la sua ‘semplicità’ [sono necessarie operazioni aritmetiche elementari…] ma nasconde due grosse ‘insidie’...
In primo luogo prendiamo in esame la $Y(z)$. Se $Y(z)$ è lunga $n$ campioni essa è un polinomio di grado $n-1$ e occorre isolare tutte le sue $n-1$ radici. Se si tratta di una brano musicale di un’ora registrato a 50.000 campioni al secondo $n$ vale $1.8*10^8$…
In secondo luogo che cosa si fa se una delle radici di $H$ o di $Y$ ha modulo esattamente uguale a 1?… Darà contributo a fase minima o massima?…
Più avanti cercheremo di trovare soluzione a queste due ‘insidie’. Per il momento c’è qualcuno che ha qualche 'critica' da fare a come ho fatto fin qui?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Intanto vale sempre l’ipotesi che il filtro che si deve ‘invertire’ abbia risposta all’impulso finita. Nello scorso postato abbiamo visto che per una qualunque z-trasformata $H(z)$ di soli zeri possiamo scrivere…
$H(z)=H_p(z)*H_q(z)$ (1)
… ove con $H_p$ e $H_q$ si intendono le componenti di $H$ rispettivamente ‘a fase minima’ e ‘a fase massima’. Di conseguenza la relazione ingresso/uscita del sistema seguente…
… potrà essere scritta come…
$Y=Y_p*Y_q= H_p*H_q*X_p*X_q$ (2)
… dove è evidente che è…
$Y_p=H_p*X_p$, $Y_q=H_q*X_q$ (3)
Le semplici equazioni (3) sono assai utili perchè dimostrano che le componenti a fase minima e fase massima di $Y$ possono essere trattate separatamente. Dal momento che sappiamo che una funzione FIR a fase minima è invertibile possiamo senz’altro scrivere…
$X_p=H_p^(-1)*Y_p$ (4)
Per quanto riguarda le componenti a fase massima invece occorre prendere una strada differente. Dal momento che una sequenza a fase massima può essere trasformata a fase minima con l’operazione di inversione possiamo scrivere…
$Inv[Y_q]= Inv[H_q]*Inv[X_q]$ (5)
… da cui con un poco si passaggi si ottiene…
$X_q= Inv[Inv^(-1)[H_q]*Inv[Y_q]]$ (6)
Una volta note $X_p$ e $X_q$ è immediato trovare…
$X(z)=X_p(z)*X_q(z)$ (7)
La procedura per realizzare il filtro inverso di una $H(z)$ qualunque può essere dunque ipotizzato nel seguente modo…
a) si scompongono in fattori le due sequenze $H(z)$ e $Y(z)$
b) si separano le componenti a fase minima e massima di $H(z)$ e $Y(z)$
c) si calcola $X_p$ con la (4)
d) si calcola $X_q$ con la (5)
e) si calcola $X$ con la (7)
Il metodo è certo attraente per la sua ‘semplicità’ [sono necessarie operazioni aritmetiche elementari…] ma nasconde due grosse ‘insidie’...
In primo luogo prendiamo in esame la $Y(z)$. Se $Y(z)$ è lunga $n$ campioni essa è un polinomio di grado $n-1$ e occorre isolare tutte le sue $n-1$ radici. Se si tratta di una brano musicale di un’ora registrato a 50.000 campioni al secondo $n$ vale $1.8*10^8$…
In secondo luogo che cosa si fa se una delle radici di $H$ o di $Y$ ha modulo esattamente uguale a 1?… Darà contributo a fase minima o massima?…
Più avanti cercheremo di trovare soluzione a queste due ‘insidie’. Per il momento c’è qualcuno che ha qualche 'critica' da fare a come ho fatto fin qui?…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
"lupo grigio":
Per il momento c’è qualcuno che ha qualche 'critica' da fare a come ho fatto fin qui?…
Perché scomponi anche Y(z) nelle 2 componenti?
Beh!... in sostanza la $Y_p$ contiene informazioni sulla componenti 'a fase minima' $X_p$ e la $Y_q$ contiene informazioni sulla componente 'a fase massima' $X_q$. Per ottenere entrambe devo di necessità separarle... o no?...
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
temo non ci sia bisogno, tant'è che non si fattorizzano polinomi con milioni di termini
Ragazzi
vediamo di riprendere il discorso sul ‘filtro inverso’, cha ho [colpevolmente…] lasciato da parte per seguire altre strade, cercando bene si separare i problemi rimasti aperti…
a) che fare con le funzioni che hanno zeri sul cerchio unitario e quindi non sono ‘trattabili’ né come ‘a fase minima’ né come ‘a fase massima’
b) che fare con le sequenze di lunghezza elevata
Affrontiamo da prima il ‘problema a’. Se supponiamo che il blocco H abbia risposta all’impulso finita di lunghezza $N$ essa è esprimibile in forma di z-trasformata come…
$H(z)= h_0*(1- r_1*z^(-1))*(1-r_2*z^(-1))*...*(1-r_(N-1)*z(-1))$ (1)
… essendo le $r_i$, $i=1,2,…, N-1$ gli ‘zeri’ della $H(z)$. Ora abbiamo visto che se per tutte le $r_i$ è $|r_i|<1$ o $|r_i|>1$ la $H(z)$ può essere scomposta in due copmpeoenti ciascuna delle quali è invertibile. Se viceversa per una o più delle $r_i$ è $|r_i|=1$ allora si può vedere facilmente che la $H(z)$ non è invertibile. Che si fa allora?…
Senza lasciarci prendere dallo sconforto proviamo a scrivere nuovamente la relazione ingresso uscita per un sistema a risposta finita…
$y(n)= sum_(i=0)^(N-1) h_i*x(n-i)$ (2)
… che in termini di z-trasformata diviene…
$Y(z)= H(z)*X(z)$ (3)
Se la sequenza $x(n)$ ha lunghezza finita M e $h(n)$ ha lunghezza finita N allora la sequenza $y(n)$ avrà lunghezza finita $M+N-1$… non è vero?… In particolare se fattorizziamo sia $X(z)$ sia $H(z)$ la (3) diviene…
$Y(z)= h_0*(1-r_1*z^(-1))*(1-r_2*z^(-1)*…*(1-r_(N-1)*z^(-1))*$
$*x_0*(1-alpha_1*z^(-1))*(1-alpha_2*z^(-1))*…*(1-alpha_(M-1)*z^(-1))$ (4)
Dal momento che sia $H(z)$ sia $Y(z)$ sono noti e che le $r_i$ sono zeri di entrambi, la soluzione generale del problema potrebbe risiedere nella seguente procedura…
a) si sviluppa $H(z)$ in fattori
b) si sviluppa $Y(z)$ in fattori
c) si forma il polinomio $X(z)$ eliminando da $Y(z)$ i fattori che esso ha in comune con $H(z)$ e dividendo per $h_0$
Semplice no?… almeno dal punto di vista ‘concettuale’… voi che ne dite?…
cordiali saluti
lupo grigio

an old wolf may lose his teeth, but never his nature
vediamo di riprendere il discorso sul ‘filtro inverso’, cha ho [colpevolmente…] lasciato da parte per seguire altre strade, cercando bene si separare i problemi rimasti aperti…
a) che fare con le funzioni che hanno zeri sul cerchio unitario e quindi non sono ‘trattabili’ né come ‘a fase minima’ né come ‘a fase massima’
b) che fare con le sequenze di lunghezza elevata
Affrontiamo da prima il ‘problema a’. Se supponiamo che il blocco H abbia risposta all’impulso finita di lunghezza $N$ essa è esprimibile in forma di z-trasformata come…
$H(z)= h_0*(1- r_1*z^(-1))*(1-r_2*z^(-1))*...*(1-r_(N-1)*z(-1))$ (1)
… essendo le $r_i$, $i=1,2,…, N-1$ gli ‘zeri’ della $H(z)$. Ora abbiamo visto che se per tutte le $r_i$ è $|r_i|<1$ o $|r_i|>1$ la $H(z)$ può essere scomposta in due copmpeoenti ciascuna delle quali è invertibile. Se viceversa per una o più delle $r_i$ è $|r_i|=1$ allora si può vedere facilmente che la $H(z)$ non è invertibile. Che si fa allora?…
Senza lasciarci prendere dallo sconforto proviamo a scrivere nuovamente la relazione ingresso uscita per un sistema a risposta finita…
$y(n)= sum_(i=0)^(N-1) h_i*x(n-i)$ (2)
… che in termini di z-trasformata diviene…
$Y(z)= H(z)*X(z)$ (3)
Se la sequenza $x(n)$ ha lunghezza finita M e $h(n)$ ha lunghezza finita N allora la sequenza $y(n)$ avrà lunghezza finita $M+N-1$… non è vero?… In particolare se fattorizziamo sia $X(z)$ sia $H(z)$ la (3) diviene…
$Y(z)= h_0*(1-r_1*z^(-1))*(1-r_2*z^(-1)*…*(1-r_(N-1)*z^(-1))*$
$*x_0*(1-alpha_1*z^(-1))*(1-alpha_2*z^(-1))*…*(1-alpha_(M-1)*z^(-1))$ (4)
Dal momento che sia $H(z)$ sia $Y(z)$ sono noti e che le $r_i$ sono zeri di entrambi, la soluzione generale del problema potrebbe risiedere nella seguente procedura…
a) si sviluppa $H(z)$ in fattori
b) si sviluppa $Y(z)$ in fattori
c) si forma il polinomio $X(z)$ eliminando da $Y(z)$ i fattori che esso ha in comune con $H(z)$ e dividendo per $h_0$
Semplice no?… almeno dal punto di vista ‘concettuale’… voi che ne dite?…
cordiali saluti
lupo grigio

an old wolf may lose his teeth, but never his nature


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo