Elementi invertibili
Sapete quali sono gli elementi invertibili rispetto al prodotto in :
Z7[x] , Q[x] , C(complessi) ???
se lo sapete elencatemeli , grazie !!!
Z7[x] , Q[x] , C(complessi) ???
se lo sapete elencatemeli , grazie !!!
Risposte
Nessuno sa dirmelo ?
C e' un campo, per cui tutti gli elementi tranne lo zero sono invertibili.
Z_7[x] e' l'anello dei polinomi a coefficienti in Z_7. Elencare gli elementi non invertibili mi sembra eccessivo, a meno che non siano pochi per il fatto che 7 e' primo (Z_7 e' un campo). Stessa cosa vale per Q[x]. Provero' a riguardare un po' di teoria.
Luca Lussardi
http://www.llussardi.it
Z_7[x] e' l'anello dei polinomi a coefficienti in Z_7. Elencare gli elementi non invertibili mi sembra eccessivo, a meno che non siano pochi per il fatto che 7 e' primo (Z_7 e' un campo). Stessa cosa vale per Q[x]. Provero' a riguardare un po' di teoria.
Luca Lussardi
http://www.llussardi.it
Il problema di trovare i polinomi invertibili in Z|p| si può affrontare generalizzando il procedimento usato per p=2 illustrato in https://www.matematicamente.it/forum/top ... IC_ID=5586 …
Fissato un polinomio generatore g(x) = g(o) + g(1) x + g(2) x^2 +… +g(n) x^n di grado n e indicato a(x)= ao + a1 x + a(2) x^2… + a(n-1) x^(n-1) un generico polinomio di grado n-1 ‘modulo g(x)’, l’insieme dei polinomi invertibili è generato dallo shift register illustrato nella figura qui sotto, caricato inizialmente con x^o = 1…
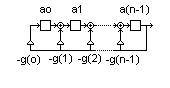
Il numero di essi è dato dalle distinte potenze di x ‘modulo g(x)’ e tale numero dipende strettamente dalla scelta di g(x). Indicato con M il numero di potenze distinte di x, il massimo possibile valore di M è chiaramente pari a p^(n-1)-1 [ossia l’intero insieme degli a(x) ad eccezione del polinomio nullo…]. Definito con x^k [k=o,1,…, M-1] un generico polinomio invertibile, il polinomio inverso è dato da x^(M-k). Non so se esiste un criterio particolare per trovare un polinomio che dia il massimo valore possibile di M. In pratica conviene forse procedere per tentativi. Nel caso p=7 ed n=2 [massimo valore di M pari a 48], con pochi tentativi ho trovato un polinomio generatore g(x) che genera i seguenti 42 [massimo valore di M= 48] polinomi invertibili…
g(x) = 4 + 4x + x^2
x^o = 1
x^1= x
x^2=3+3x
x^3=2+5x
x^4=1+3x
x^5=2+3x
x^6=2+4x
x^7=5
x^8=5x
x^9=1+x
x^10=3+4x
x^11=5+x
x^12=3+x
x^13=3+6x
x^14=4
x^15=4x
x^16=5+5x
x^17=1+6x
x^18=4+5x
x^19=1+5x
x^20=1+2x
x^21=6
x^22=6x
x^23=4+4x
x^24=5+2x
x^25=6+4x
x^26=5+4x
x^27=5+3x
x^28=2
x^29=2x
x^30=6+6x
x^31=4+3x
x^32=2+6x
x^33=4+6x
x^34=4+x
x^35=3
x^36=3x
x^37=2+2x
x^38=6+x
x^39=3+2x
x^40=6+2x
x^41=6+5x
Naturalmente non è escluso si trovi anche un polinomio g(x) che generi tutti e 48 i polinomi diversi dal polinomio nullo… tutto sta a cercarlo…
cordiali saluti
lupo grigio

Fissato un polinomio generatore g(x) = g(o) + g(1) x + g(2) x^2 +… +g(n) x^n di grado n e indicato a(x)= ao + a1 x + a(2) x^2… + a(n-1) x^(n-1) un generico polinomio di grado n-1 ‘modulo g(x)’, l’insieme dei polinomi invertibili è generato dallo shift register illustrato nella figura qui sotto, caricato inizialmente con x^o = 1…

Il numero di essi è dato dalle distinte potenze di x ‘modulo g(x)’ e tale numero dipende strettamente dalla scelta di g(x). Indicato con M il numero di potenze distinte di x, il massimo possibile valore di M è chiaramente pari a p^(n-1)-1 [ossia l’intero insieme degli a(x) ad eccezione del polinomio nullo…]. Definito con x^k [k=o,1,…, M-1] un generico polinomio invertibile, il polinomio inverso è dato da x^(M-k). Non so se esiste un criterio particolare per trovare un polinomio che dia il massimo valore possibile di M. In pratica conviene forse procedere per tentativi. Nel caso p=7 ed n=2 [massimo valore di M pari a 48], con pochi tentativi ho trovato un polinomio generatore g(x) che genera i seguenti 42 [massimo valore di M= 48] polinomi invertibili…
g(x) = 4 + 4x + x^2
x^o = 1
x^1= x
x^2=3+3x
x^3=2+5x
x^4=1+3x
x^5=2+3x
x^6=2+4x
x^7=5
x^8=5x
x^9=1+x
x^10=3+4x
x^11=5+x
x^12=3+x
x^13=3+6x
x^14=4
x^15=4x
x^16=5+5x
x^17=1+6x
x^18=4+5x
x^19=1+5x
x^20=1+2x
x^21=6
x^22=6x
x^23=4+4x
x^24=5+2x
x^25=6+4x
x^26=5+4x
x^27=5+3x
x^28=2
x^29=2x
x^30=6+6x
x^31=4+3x
x^32=2+6x
x^33=4+6x
x^34=4+x
x^35=3
x^36=3x
x^37=2+2x
x^38=6+x
x^39=3+2x
x^40=6+2x
x^41=6+5x
Naturalmente non è escluso si trovi anche un polinomio g(x) che generi tutti e 48 i polinomi diversi dal polinomio nullo… tutto sta a cercarlo…
cordiali saluti
lupo grigio

E voilà!… ecco trovato un polinomio generatore che genera tutti e 48 i polinomi non nulli!…
g(x)= 5 + 3x + x^2
x^o=1
x^1=x
x^2=2+4x
x^3=1+4x
x^4=1+3x
x^5=6+6x
x^6=5+2x
x^7=4+6x
x^8=5
x^9=5x
x^10=3+6x
x^11=5+6x
x^12=5+x
x^13=2+2x
x^14=4+3x
x^15=6+2x
x^16=4
x^17=4x
x^18=1+2x
x^19=4+2x
x^20=4+5x
x^21=3+3x
x^22=6+x
x^23=2+3x
x^24=6
x^25=6x
x^26=5+3x
x^27=6+3x
x^28=6+4x
x^29=1+x
x^30=2+5x
x^31=3+x
x^32=2
x^33=2x
x^34=4+x
x^35=2+x
x^36=2+6x
x^37=5+5x
x^38=3+4x
x^39=1+5x
x^40=3
x^41=3x
x^42=6+5x
x^43=3+5x
x^44=3+2x
x^45=4+4x
x^46=1+6x
x^47=5+4x
cordiali saluti
lupo grigio

g(x)= 5 + 3x + x^2
x^o=1
x^1=x
x^2=2+4x
x^3=1+4x
x^4=1+3x
x^5=6+6x
x^6=5+2x
x^7=4+6x
x^8=5
x^9=5x
x^10=3+6x
x^11=5+6x
x^12=5+x
x^13=2+2x
x^14=4+3x
x^15=6+2x
x^16=4
x^17=4x
x^18=1+2x
x^19=4+2x
x^20=4+5x
x^21=3+3x
x^22=6+x
x^23=2+3x
x^24=6
x^25=6x
x^26=5+3x
x^27=6+3x
x^28=6+4x
x^29=1+x
x^30=2+5x
x^31=3+x
x^32=2
x^33=2x
x^34=4+x
x^35=2+x
x^36=2+6x
x^37=5+5x
x^38=3+4x
x^39=1+5x
x^40=3
x^41=3x
x^42=6+5x
x^43=3+5x
x^44=3+2x
x^45=4+4x
x^46=1+6x
x^47=5+4x
cordiali saluti
lupo grigio

Gli elementi invertibili di un anello di polinomi su un dominio A sono gli invertibili di A: si dimostra facilmente usando le proprietà del grado di un polinomio. Z_7 è un campo, quindi un dominio; dunque gli invertibili di Z_7[x] sono tutti e soli gli elementi di Z_7.
Saluti,
Woody
Saluti,
Woody
mm.. non capisco la soluzione di lupogrigio.. come dice Woody, gli invertibili in Z7[x] sono tutti e soli gli elementi di Z7; questo può essere visto osservando che Zp[x] è un dominio euclideo e quindi gli invertibili sono tutti e soli quelli a valutazione minima (in questo caso la valutazione coincide col grado del polinomio) e pertanto tutte le costanti. Discorso analogo vale per Q[x] dove tutti gli invertibili sono le costanti.
ciao, ubermensch
ciao, ubermensch
Scusa Valerio (off topic), ogni tanto puoi controllare anche la posta? Thanks. [;)]
RISPONDO OFF TOPIC ALL'OFF TOPIC: HO VISTO TUTTO MA IN QUESTI GIORNI NON HO AVUTO TEMPO PER RISPONDERTI; LO FARò APPENA POSSIBILE.
CIAO
CIAO
Grazie Valerio, ciao.
In effetti leggendo il postato iniziale la mia attenzione si è ‘polarizzata’ sulla discussione precedente avviata in https://www.matematicamente.it/forum/top ... IC_ID=5586 , nella quale all’inizio di chiedeva il calcolo dell’inverso del polinomio p(x)=x nel campo dei polinomi con coefficienti reali ‘modulo g(x)= x^2+x+1’. L’esistenza di un inverso per tutti gli elementi diversi dall’elemento nullo è una delle condizioni necessarie per definire un campo, come risulta da Wikipedia…
In generale In matematica un campo è un insieme F munito di due operazioni binarie, che chiamiamo somma e prodotto e indichiamo rispettivamente con + e * , che godono delle seguenti proprietà:
a) per ogni coppia di elementi a,b appartenenti a F, la loro somma a + b appartiene a F. Si dice che F è chiuso rispetto alla somma…
b) la somma è associativa, cioè per ogni terna di elementi a,b,c appartenenti a F, vale: (a + b) + c = a + (b + c)…
c) esiste un unico elemento z appartenente a F neutro ripetto alla somma, cioè tale che a + z = z + a = a…
d) per ogni elemento a di F esiste un elemento opposto b tale che a + b = z…
e) la somma è commutativa, cioè per ogni coppia di elementi a,b di F, vale: a + b = b + a…
f) per ogni coppia di elementi a,b appartenenti a F, il loro prodotto a * b appartiene a F. Si dice che F è chiuso rispetto al prodotto…
g) il prodotto è associativo. Per ogni terna di elementi a,b,c appartenenti a F, vale: (a * b) * c = a * (b * c)…
h) esiste un unico elemento e [diverso da z] appartenente a F neutro rispetto al prodotto, cioè tale che a * e = e * a = a…
i) per ogni elemento a diverso da z esiste un elemento inverso b tale che a * b = e…
l) il prodotto è commutativo. Per ogni coppia di elementi a,b di F, vale: a * b = b * a…
m) somma e prodotto godono delle proprietà distributive. Per ogni terna a,b,c di elementi di F vale: a * (b + c) = a * b + a * c…
Naturalmente tali proprietà algebriche costituiscono il nocciolo della teoria dei campi, di enorme e insostituibile importanza sul piano applicativo. La proprietà i) stabilisce senza eccezioni che ogni elemento del campo, ad eccezione dell’elemento nullo, deve avere l’inverso moltiplicativo. Naturalmente questo è valido anche per i polinomi i cui coefficienti sono costituiti dall’insieme degli ‘interi modulo p’, denominati [se ho inteso bene…] Z|p|. L’esempio di campo da me esaminato è costruito dai polinomi ‘modulo g(x)’ con coefficienti in Z|7| e g(x) di grado 2. In pratica si tratta dell’insieme dei polinomi di grado 1 aventi ‘polinomio generatore’ g(x) di grado 2, in tutto 49 polinomi. Non tutti i polinomi g(x) di grado due con coefficienti in Z|7| diversi dal polinomio nullo [in totale 342…] sono in grado di generare un campo del tipo GF (7^2). Uno di essi è quello da me trovato, vale a dire g(x)= 5+3x+x^2. Se volete, giusto per divertirsi un poco, si possono trovare tutti gli altri…
cordiali saluti
lupo grigio

In generale In matematica un campo è un insieme F munito di due operazioni binarie, che chiamiamo somma e prodotto e indichiamo rispettivamente con + e * , che godono delle seguenti proprietà:
a) per ogni coppia di elementi a,b appartenenti a F, la loro somma a + b appartiene a F. Si dice che F è chiuso rispetto alla somma…
b) la somma è associativa, cioè per ogni terna di elementi a,b,c appartenenti a F, vale: (a + b) + c = a + (b + c)…
c) esiste un unico elemento z appartenente a F neutro ripetto alla somma, cioè tale che a + z = z + a = a…
d) per ogni elemento a di F esiste un elemento opposto b tale che a + b = z…
e) la somma è commutativa, cioè per ogni coppia di elementi a,b di F, vale: a + b = b + a…
f) per ogni coppia di elementi a,b appartenenti a F, il loro prodotto a * b appartiene a F. Si dice che F è chiuso rispetto al prodotto…
g) il prodotto è associativo. Per ogni terna di elementi a,b,c appartenenti a F, vale: (a * b) * c = a * (b * c)…
h) esiste un unico elemento e [diverso da z] appartenente a F neutro rispetto al prodotto, cioè tale che a * e = e * a = a…
i) per ogni elemento a diverso da z esiste un elemento inverso b tale che a * b = e…
l) il prodotto è commutativo. Per ogni coppia di elementi a,b di F, vale: a * b = b * a…
m) somma e prodotto godono delle proprietà distributive. Per ogni terna a,b,c di elementi di F vale: a * (b + c) = a * b + a * c…
Naturalmente tali proprietà algebriche costituiscono il nocciolo della teoria dei campi, di enorme e insostituibile importanza sul piano applicativo. La proprietà i) stabilisce senza eccezioni che ogni elemento del campo, ad eccezione dell’elemento nullo, deve avere l’inverso moltiplicativo. Naturalmente questo è valido anche per i polinomi i cui coefficienti sono costituiti dall’insieme degli ‘interi modulo p’, denominati [se ho inteso bene…] Z|p|. L’esempio di campo da me esaminato è costruito dai polinomi ‘modulo g(x)’ con coefficienti in Z|7| e g(x) di grado 2. In pratica si tratta dell’insieme dei polinomi di grado 1 aventi ‘polinomio generatore’ g(x) di grado 2, in tutto 49 polinomi. Non tutti i polinomi g(x) di grado due con coefficienti in Z|7| diversi dal polinomio nullo [in totale 342…] sono in grado di generare un campo del tipo GF (7^2). Uno di essi è quello da me trovato, vale a dire g(x)= 5+3x+x^2. Se volete, giusto per divertirsi un poco, si possono trovare tutti gli altri…
cordiali saluti
lupo grigio

Se la cosa vi può interessare ho eseguito, modificando leggermente un vecchio programma che non usavo più da qualche anno, una ricerca sistematica di tutti i polinomi di grado due in grado di generare un campo completo [49 elementi]in Z7 [x]. Limitandosi a quelli che hanno il coefficiente di x^2 uguale ad 1, essi sono in totale 8...
3+x+x^2
3+2x+x^2
5+2x+x^2
5+3x+x^2
5+4x+x^2
3+5x+x^2
5+5x+x^2
3+6x+x^2
cordiali saluti
lupo grigio

3+x+x^2
3+2x+x^2
5+2x+x^2
5+3x+x^2
5+4x+x^2
3+5x+x^2
5+5x+x^2
3+6x+x^2
cordiali saluti
lupo grigio

"Woody":
Gli elementi invertibili di un anello di polinomi su un dominio A sono gli invertibili di A: si dimostra facilmente usando le proprietà del grado di un polinomio. Z_7 è un campo, quindi un dominio; dunque gli invertibili di Z_7[x] sono tutti e soli gli elementi di Z_7.
Saluti,
Woody
Riguardo a questo , io ho una dimostrazione che dice:
Cor. Se R è un dominio di integrità, gli elementi inveribili di $R[x]$ sono tutti e soli gli elementi inveribili di R; in particolar se F è un campo gli elementi invertibili di F[x] sono tutte e sole le costanti non nulle.
dim.
Se un elemento di R è invertibile, è invertibile in $R[x]$ , poichè R coincide con $R[x]$.Viceversa, se f è un polinomio invertibile di $R[x]$, esiste un polinomio g tale che $fg=1$. Per la regola di addizione dei gradi risulta $delta(fg)=delta(f)+delta(g)=delta(1)=0$, dunque $delta(f)=delta(g)=0$ e f e g sono elementi invertibili in R.
Potresti chiarirmi la dimostrazione


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo