Diagramma di Hasse
Sia $(A,-<)$ un insieme ordinato.
Il diagramma di Hasse è un diagramma costituito da punti e linee. I punti rappresentano gli elementi di A. Ogni volta che $a-
ora devo disegnare il diagramma di Hasse di $(S,-<)$, dove $S={a in NN^{**}:a<=12}$ e la relazione $-<$ è definita su $NN^{**}$ ponendo
$a-
Io ho disegnato il seguente diagramma di Hasse:
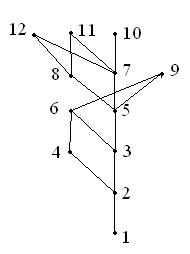
Ora, ad esempio, 6 è in relazione con 12? Devo congiungerli? Posso saltare di due livelli?
Grazie a tutti!
Il diagramma di Hasse è un diagramma costituito da punti e linee. I punti rappresentano gli elementi di A. Ogni volta che $a-
ora devo disegnare il diagramma di Hasse di $(S,-<)$, dove $S={a in NN^{**}:a<=12}$ e la relazione $-<$ è definita su $NN^{**}$ ponendo
$a-
Io ho disegnato il seguente diagramma di Hasse:
Ora, ad esempio, 6 è in relazione con 12? Devo congiungerli? Posso saltare di due livelli?
Grazie a tutti!
Risposte
Nessuno di buona volontà???
6 è certamente in relazione con 12, perchè: 6*4 = 24 < 36 = 3*12 . Ma non capisco alcune cose:
(1) Se $a < b$ , allora $a$ deve essere disegnato esattamente sotto $b$ ?
(2) Non è possibile che esistano due segmenti che congiungono 12 a due numeri distinti, in questo caso 8 e 7: va contro la convenzione:
(1) Se $a < b$ , allora $a$ deve essere disegnato esattamente sotto $b$ ?
(2) Non è possibile che esistano due segmenti che congiungono 12 a due numeri distinti, in questo caso 8 e 7: va contro la convenzione:
"leonardo":
Se non esiste un c $\in$ A:a.
Non credo che tu possa congiungere 12 e 6, perchè: 4*7 = 28 < 36 = 12*3 .
Ok. A questo ci avevo pensato! Ma allora il diagramma che ho disegnato va bene?
Grazie ancora!
Grazie ancora!
Non credo, perchè hai congiunto 7 e 8 a 12.
PS: ho corretto il mio post precedente.
PS: ho corretto il mio post precedente.
Si, quello è giusto! Infatti 7 è in relazione con 12 e 8 è in relazione con 12. Questo non è un errore!
Se non ci sono elementri tra 6 e 12 devi congiungerlin anche se salti di due livelli. E' irrilevante di quanti livelli si salta.
Quindi nel diagramma mancano molti segmenti! 6 e 12, 6 e 10, 4 e 7, 4 e 9, 4 e 8, etc. Come lo disegno?
Si devi mettere anche questi spigoli...
In pratica nel diagramma ci sono tutte le connessioni se e solo se per ogni $a,b$ con $a
Quindi il diagramma che hai disegnato all'inizio non completo. Infatti non posso congiungere, per esempio, 7 con 4 con un percorso discendente.
In pratica nel diagramma ci sono tutte le connessioni se e solo se per ogni $a,b$ con $a
Quindi il diagramma che hai disegnato all'inizio non completo. Infatti non posso congiungere, per esempio, 7 con 4 con un percorso discendente.
Si ma praticamente il diagramma completo qual è? Io non riesco a disegnarlo!
Grazie ancora!
Grazie ancora!
purtroppo non so come si scrivono i grafi in questo forum  ! se ci sono delle istruzioni da qualche parte te lo disegno!
! se ci sono delle istruzioni da qualche parte te lo disegno!
Ficus ti ringrazio ancora per la tua disponibilità! Comunque con un po' di buona volonta si disegna facilmente con Paint!
L'ho disegnato...come faccio a fartelo avere?
Puoi mandarmelo per email! Ti ringrazio molto!
Ciao, a presto!
Ciao, a presto!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo