Calendario incontri di gruppo
Salve a tutti gli appassionati di questo sito
da un pò sbatto con un problema che ritengo/spero si possa risolvere facilmente con l'aiuto di qualche formula o algoritmo matematico.
Devo scrivere il calendario per fare incontrare tra di loro 21 persone suddivise in 5 gruppi.
Ogni gruppo quindi sarà formato da 4 persone (tranne uno che sarà di 5).
L'obiettivo è fare ruotare le persone in modo che possano incontrare tutti nel minor tempo possibile.
Ogni gruppo ha 1 persona-guida che non ruota, ma rimane fissa nel gruppo
(questo in effetti è una condizione che potrebbe anche essere superata).
Chiaro il problema? Cosa suggerite?
grazie
Pino
p.s. chiedo venia agli amministratori se ho sbagliato sezione spostatemi tranquillamente (tanto a furia di sbattere con questo problema sono già un pò "spostato"
da un pò sbatto con un problema che ritengo/spero si possa risolvere facilmente con l'aiuto di qualche formula o algoritmo matematico.
Devo scrivere il calendario per fare incontrare tra di loro 21 persone suddivise in 5 gruppi.
Ogni gruppo quindi sarà formato da 4 persone (tranne uno che sarà di 5).
L'obiettivo è fare ruotare le persone in modo che possano incontrare tutti nel minor tempo possibile.
Ogni gruppo ha 1 persona-guida che non ruota, ma rimane fissa nel gruppo
(questo in effetti è una condizione che potrebbe anche essere superata).
Chiaro il problema? Cosa suggerite?
grazie
Pino
p.s. chiedo venia agli amministratori se ho sbagliato sezione spostatemi tranquillamente (tanto a furia di sbattere con questo problema sono già un pò "spostato"
Risposte
Rientro dopo qualche giorno di relax e trovo l'intervento di onlyReferee che ringrazio insieme ad Alex per l'interessamento.
Come dicevo precedentemente non sono un matematico...
Vorrei provare a semplificare un pò il problema togliendo alcuni vincoli che penso di potere superare:
20 persone che si devono incontrare in gruppi di 5
in modo che ognuno possa incontrare tutti nel più breve tempo possibile.
Su questo sito http://utenti.quipo.it/base5/combinatoria/calcombinat.htm ho trovato la formula
e l'elenco delle combinazioni possibili (4845).
Ma quello che desidererei trovare è una formula, un metodo, un algoritmo, un programma che analizzi con criterio queste combinazioni e scelga quelle che creano meno ridondanze.
Mi ero entusiasmato quando onlyReferee aveva detto che esiste almeno una soluzione.
Ma anche se non esiste, l'obiettivo è di fare incontrare tutti con tutti, anche se qualcuno si incontra più di una volta.
Quindi umilmente chiedo: come posso scegliere da questo elenco le combinazioni che creano meno ridondanza di incontro?
grazie
Come dicevo precedentemente non sono un matematico...
Vorrei provare a semplificare un pò il problema togliendo alcuni vincoli che penso di potere superare:
20 persone che si devono incontrare in gruppi di 5
in modo che ognuno possa incontrare tutti nel più breve tempo possibile.
Su questo sito http://utenti.quipo.it/base5/combinatoria/calcombinat.htm ho trovato la formula
e l'elenco delle combinazioni possibili (4845).
Ma quello che desidererei trovare è una formula, un metodo, un algoritmo, un programma che analizzi con criterio queste combinazioni e scelga quelle che creano meno ridondanze.
Mi ero entusiasmato quando onlyReferee aveva detto che esiste almeno una soluzione.
Ma anche se non esiste, l'obiettivo è di fare incontrare tutti con tutti, anche se qualcuno si incontra più di una volta.
Quindi umilmente chiedo: come posso scegliere da questo elenco le combinazioni che creano meno ridondanza di incontro?
grazie
Premesso che io non me ne intendo granché quindi prendi quello che dico con beneficio d'inventario, non è una questione di umiltà ma proprio di difficoltà ... come hai già visto non sempre esiste una soluzione completa al tuo problema e paradossalmente quello che chiedi ora è più difficile da risolvere di quello originale (escludere qualcosa è più facile che trovare il minimo ...).
Detto questo un programma che faccia quello che chiedi (cioè costruisca tutte le combinazioni e selezioni quelle migliori) penso proprio che si possa costruire (e magari qualcuno l'ha già fatto ...) ma credo altrettanto che non sia banale e sia anche pesantino dal punto di vista computazionale; per esempio a me risulta (se non ho fatto cavolate
) che un sola giornata di incontri può essere formata in $11.732.745.024$ modi (che, praticamente, dovresti elevare alla quinta per trovare il totale ...): parecchi direi ... 
Cordialmente, Alex
Nota: La scelta di cinque persone prese a caso all'interno di un gruppo di venti può essere fatta in $15.504$ modi diversi, e questo è solo il primo gruppo; per ciascuno di questi modi ce ne sono $3.003$ per sceglierne altre cinque tra le quindici rimanenti, e così via ... per arrivare al totale che ho scritto sopra.
Peraltro formare la prima giornata è facilissimo, basta formarne una a caso che va sempre bene, e scegliere le altre il problema ...
Detto questo un programma che faccia quello che chiedi (cioè costruisca tutte le combinazioni e selezioni quelle migliori) penso proprio che si possa costruire (e magari qualcuno l'ha già fatto ...) ma credo altrettanto che non sia banale e sia anche pesantino dal punto di vista computazionale; per esempio a me risulta (se non ho fatto cavolate
) che un sola giornata di incontri può essere formata in $11.732.745.024$ modi (che, praticamente, dovresti elevare alla quinta per trovare il totale ...): parecchi direi ... Cordialmente, Alex
Nota: La scelta di cinque persone prese a caso all'interno di un gruppo di venti può essere fatta in $15.504$ modi diversi, e questo è solo il primo gruppo; per ciascuno di questi modi ce ne sono $3.003$ per sceglierne altre cinque tra le quindici rimanenti, e così via ... per arrivare al totale che ho scritto sopra.
Peraltro formare la prima giornata è facilissimo, basta formarne una a caso che va sempre bene, e scegliere le altre il problema ...
Ciao Alex
c'è qualcosa che non mi confinfera... introducendo nel calcolatore di cui il link sopra
n=20
K=4
ottengo:
C(20,4) [senza ripetizioni] = 4845
abcd abce abcf abcg abch abci abcj abck abcl abcm abcn abco abcp abcq abcr abcs abct abde abdf abdg abdh abdi abdj abdk abdl abdm abdn abdo abdp abdq abdr abds abdt abef abeg abeh abei abej abek abel abem aben abeo abep abeq aber abes abet abfg abfh abfi abfj abfk abfl abfm abfn abfo abfp abfq abfr...
(non continuo ma ci sono tutte le 4845 combinazioni)
Non mi è chiaro com'è che tu arrivi a quel numero così alto.
Nel frattempo ho trovato un paio di siti che "svilppano calendari per tornei di calcio, basket, pallavolo, tennis...etc"
ci vorrebbe un gioco con 4 giocatori, tipo bridge, ma in questi siti non viene contemplato...
continuo la ricerca
bye
c'è qualcosa che non mi confinfera... introducendo nel calcolatore di cui il link sopra
n=20
K=4
ottengo:
C(20,4) [senza ripetizioni] = 4845
abcd abce abcf abcg abch abci abcj abck abcl abcm abcn abco abcp abcq abcr abcs abct abde abdf abdg abdh abdi abdj abdk abdl abdm abdn abdo abdp abdq abdr abds abdt abef abeg abeh abei abej abek abel abem aben abeo abep abeq aber abes abet abfg abfh abfi abfj abfk abfl abfm abfn abfo abfp abfq abfr...
(non continuo ma ci sono tutte le 4845 combinazioni)
Non mi è chiaro com'è che tu arrivi a quel numero così alto.
Nel frattempo ho trovato un paio di siti che "svilppano calendari per tornei di calcio, basket, pallavolo, tennis...etc"
ci vorrebbe un gioco con 4 giocatori, tipo bridge, ma in questi siti non viene contemplato...
continuo la ricerca
bye
"rainbowpino":
Non mi è chiaro com'è che tu arrivi a quel numero così alto.
Leggi la nota ... e casomai chiedi ...
"rainbowpino":
Nel frattempo ho trovato un paio di siti che "svilppano calendari per tornei di calcio, basket, pallavolo, tennis...etc"
Ci ho provato anch'io ma per adesso niente ...
Cordialmente, Alex
Non sono sicuro che algebra sia così migliore di informatica su un problema di questo tipo. Comunque se il problema consiste nel trovare una soluzione minimale non serve trovarle tutte. Anche perché in un certo senso molte sono equivalenti tra di loro (producibili l'una dall'altra permutando l'insieme iniziale, permutando i gruppi tra di loro, permutando le settimane o facendo più di una di queste operazioni). In un certo senso si potrebbe cercare una soluzione comoda e poi aggiustarla in modo da renderla migliore.
Computazionalmente parlando non ha molto senso elencare tutte le possibilità. Insomma, potresti tranquillamente partire supponendo che le prime 5 giornate del primo gruppo siano le seguenti: abcd efgh ilmn opqr stuv e in generale di avere:
A questo punto si tratta di riempire i buchi. Le ultime due righe, ovvero quelle che ho lasciato completamente vuote, richiedono un po' di sforzo in più (e delle ripetizioni sono inevitabili dato che 20 non è divisibile per 3).
Computazionalmente parlando non ha molto senso elencare tutte le possibilità. Insomma, potresti tranquillamente partire supponendo che le prime 5 giornate del primo gruppo siano le seguenti: abcd efgh ilmn opqr stuv e in generale di avere:
1 abcd efgh ilmn opqr stuv **** **** 2 eios ai** ae** a**s a**o **** **** 3 flpt bl** bf** b**t b**p **** **** 4 gmqu cm** cg** c**u c**q **** **** 5 hnrv dn** dh** d**v d**r **** ****
A questo punto si tratta di riempire i buchi. Le ultime due righe, ovvero quelle che ho lasciato completamente vuote, richiedono un po' di sforzo in più (e delle ripetizioni sono inevitabili dato che 20 non è divisibile per 3).
Scusami vict85 ma una soluzione minimale che secondo me poteva andar bene glielo già data (vedi ultimo post della prima pagina) ed anche un paio di suggerimenti su come eventualmente poterla aggiustare ma mi pare di aver capito che voglia qualcosa di più stringente (altrimenti potrebbero andar bene anche i siti che stilano calendari per i vari sport).
Per quanto riguarda algebra o informatica: se la questione fosse puramente computazionale non ci sarebbe dubbio ma io conosco diversi problemi di questo tipo (come quello famoso delle 15 scolarette) risolti in maniera algebrica (anche perché non potevano fare altrimenti essendo ottocenteschi ... ) quindi pensavo nella mia ignoranza che magari oggigiorno ci fosse qualcosa di più sistematico ... oltre al computer ovviamente ... .
Cordialmente, Alex
Per quanto riguarda algebra o informatica: se la questione fosse puramente computazionale non ci sarebbe dubbio ma io conosco diversi problemi di questo tipo (come quello famoso delle 15 scolarette) risolti in maniera algebrica (anche perché non potevano fare altrimenti essendo ottocenteschi ...
) quindi pensavo nella mia ignoranza che magari oggigiorno ci fosse qualcosa di più sistematico ... oltre al computer ovviamente ... .Cordialmente, Alex
Il problema è che per certi versi non c'è alcuna soluzione al problema. Insomma a meno di casi speciali come quello di 15 persone in 5 gruppi (o equivalentemente 20 divise in 5 gruppi di 4 con 1 per gruppo fisso), non si può avere che tutti incontrino tutti gli altri esattamente una volta. In un certo senso si deve decidere se è più importante che si incontrino tutti o che si incontrino solo una volta. Intuitivamente direi che è possibile arrivare sempre ad una situazione in cui tutti si incontrino con tutti lo stesso numero di volte, ma il numero di incontri totale cresce.
Supponendo di trovarci in un caso che ammette soluzioni, il numero è tanto alto che conviene eliminare la variabilità e considerarla successivamente. Cosa che comunque fanno anche per i campionati. Per esempio, a meno di una permutazione delle squadre, la prima giornata è sostanzialmente una sola.
Supponendo di trovarci in un caso che ammette soluzioni, il numero è tanto alto che conviene eliminare la variabilità e considerarla successivamente. Cosa che comunque fanno anche per i campionati. Per esempio, a meno di una permutazione delle squadre, la prima giornata è sostanzialmente una sola.
Sono d'accordo, rimane da convincere l'autore del thread ... 
Cordialmente, Alex
Cordialmente, Alex
"axpgn":
Sono d'accordo, rimane da convincere l'autore del thread ...
Cordialmente, Alex
Ciao Alex
l'autore del thread si è convinto! confesso che non avevo approfondito la tua soluzione perchè sviato dalle evidenti ridondanze.
Ieri sera (mettendo da parte un pò della mia presunzione) ho analizzato a fondo la tua soluzione
e in effetti ho osservato che in 7 incontri il tuo schema fa incontrare tutti con quasi tutti.
Questo è lo schema. Per semplicità ho indicato tutte le persone con i numeri da 1 a 20.
I numeri all'interno delle celle indicano il numero dell'incontro in cui le persone sono insieme.
p.e. la Persona "1" si incontra con la persona "7" nell'incontro n.1;
la persona "2" si incontra con la persona "10" negli incontri n.1 e n.3
Le celle in sfondo giallo indicano che le due persone NON si sono incontrate.
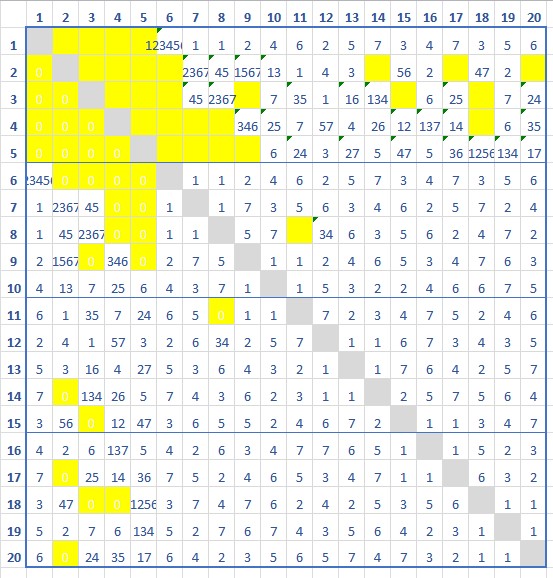
C'è da risolvere alcune ridondanze forse un pò esagerate, come "6" che si incontra sempre con "1",
o "7" che si incontra quattro volte con "2",
analogamente "8" che si incontra quattro volte con "3" e qualcun'altra.
Quindi dato che il tuo schema funziona almeno al 90% (percentuale a caso non calcolata
volevo chiederti se, nello stilare il calendario, hai usato un criterio, o sei andato a caso.
Ancora grazie e scusa se ho sottovalutato la tua proposta.
bye
Pino
Allora ... tenterò di spiegarmi ma abbiate comprensione ... 
Nel caso che avevi postato originalmente esisteva una condizone in più: i cosiddetti "capi" NON si incontravano fra loro e le ridondanze del mio esempio nascono da lì; infatti si può verificare che TUTTI i "non capi" si incontrano una e una sola volta come richiesto (fatto che io inteso come prioritario). Successivamente avevo suggerito un metodo per "mischiare" un po' più i capi con gli altri ma a parte il caso $1a$ non credo che la situazione cambi molto ... hai provato per caso anche quello?
Il fatto è che una volta appurato che, dati QUEI numeri, non esiste una soluzione "perfetta" dovresti decidere TU quale livello minimo ti aggrada ... ovviamente per quel che ne so io il mio esempio è sufficiente ma ciò non vale per te ... inoltre rimane il fatto che non sapendo (almeno io) quale sia il livello di approssimazione minimo raggiungibile anche usando un computer dovresti provarle tutte per trovare la soluzione migliore ... se invece decidi a priori quale livello vuoi raggiungere (o che ti accontenti di raggiungere) allora un programmino può essere utile (e fattibile ...).
Non sono andato a caso ... ho semplicemente copiato (o meglio, adattato ...).
Letto il tuo post, ripensandoci, mi sono ricordato di un quesito che gli era simile; purtroppo le richieste erano diverse ma ho provato ad adattarlo privilegiando quella che mi pareva la condizione più rilevante cioè far incontrare tutti gli "utenti" tra loro una volta sola ...
Cordialmente, Alex
Nel caso che avevi postato originalmente esisteva una condizone in più: i cosiddetti "capi" NON si incontravano fra loro e le ridondanze del mio esempio nascono da lì; infatti si può verificare che TUTTI i "non capi" si incontrano una e una sola volta come richiesto (fatto che io inteso come prioritario). Successivamente avevo suggerito un metodo per "mischiare" un po' più i capi con gli altri ma a parte il caso $1a$ non credo che la situazione cambi molto ... hai provato per caso anche quello?
Il fatto è che una volta appurato che, dati QUEI numeri, non esiste una soluzione "perfetta" dovresti decidere TU quale livello minimo ti aggrada ... ovviamente per quel che ne so io il mio esempio è sufficiente ma ciò non vale per te ... inoltre rimane il fatto che non sapendo (almeno io
) quale sia il livello di approssimazione minimo raggiungibile anche usando un computer dovresti provarle tutte per trovare la soluzione migliore ... se invece decidi a priori quale livello vuoi raggiungere (o che ti accontenti di raggiungere) allora un programmino può essere utile (e fattibile ...).Non sono andato a caso ... ho semplicemente copiato
(o meglio, adattato ...).Letto il tuo post, ripensandoci, mi sono ricordato di un quesito che gli era simile; purtroppo le richieste erano diverse ma ho provato ad adattarlo privilegiando quella che mi pareva la condizione più rilevante cioè far incontrare tutti gli "utenti" tra loro una volta sola ...
Cordialmente, Alex
Rielaborando ancora un pochino il primo schema sono giunto a questo prospetto:
1° giorno: $1abc\ \ \ 2def\ \ \ 3ghi\ \ \ 4jkl\ \ \ 5mno$
2° giorno: $3adg\ \ \ 2bkn\ \ \ 4col\ \ \ 5jei\ \ \ 1mhf$
3° giorno: $3ajm\ \ \ 5beh\ \ \ 4cfi\ \ \ 1dko\ \ \ 2gnl$
4° giorno: $4aek\ \ \ 2cgm\ \ \ 3boi\ \ \ 5dhl\ \ \ 1jnf$
5° giorno: $4ahn\ \ \ 5cdj\ \ \ 3bfl\ \ \ 1g\e\o\ \ \ 2mki$
6° giorno: $2afo\ \ \ 4bgj\ \ \ 3ckh\ \ \ 1dni\ \ \ 5mel$
7° giorno: $1ail\ \ \ 4bdm\ \ \ 3cen\ \ \ 5gkf\ \ \ 2jho$
C'è un solo "buco" e solo un caso triplicato (gli altri al massimo duplicati), sempre con la premessa che i "capi" non si incontrino ... difficile fare di più (almeno per me ... )
Cordialmente, Alex
1° giorno: $1abc\ \ \ 2def\ \ \ 3ghi\ \ \ 4jkl\ \ \ 5mno$
2° giorno: $3adg\ \ \ 2bkn\ \ \ 4col\ \ \ 5jei\ \ \ 1mhf$
3° giorno: $3ajm\ \ \ 5beh\ \ \ 4cfi\ \ \ 1dko\ \ \ 2gnl$
4° giorno: $4aek\ \ \ 2cgm\ \ \ 3boi\ \ \ 5dhl\ \ \ 1jnf$
5° giorno: $4ahn\ \ \ 5cdj\ \ \ 3bfl\ \ \ 1g\e\o\ \ \ 2mki$
6° giorno: $2afo\ \ \ 4bgj\ \ \ 3ckh\ \ \ 1dni\ \ \ 5mel$
7° giorno: $1ail\ \ \ 4bdm\ \ \ 3cen\ \ \ 5gkf\ \ \ 2jho$
C'è un solo "buco" e solo un caso triplicato (gli altri al massimo duplicati), sempre con la premessa che i "capi" non si incontrino ... difficile fare di più (almeno per me ...
)Cordialmente, Alex
"axpgn":
Non sono andato a caso ... ho semplicemente copiato
Letto il tuo post, ripensandoci, mi sono ricordato di un quesito che gli era simile; purtroppo le richieste erano diverse ma ho provato ad adattarlo privilegiando quella che mi pareva la condizione più rilevante cioè far incontrare tutti gli "utenti" tra loro una volta sola ...
Cordialmente, Alex
grazie Alex
vedo che hai creato un'altra combinazione in poco tempo (io per ogni tentativo ci impiego ore e ore)
posso chiederti nuovamente che metodo hai usato o se ti sei avvalso di qualche programma?
Riguardo la condizione dei "capi" non è un elemento assoluto, nel senso che è una condizione che dovrei cercare di mantenere necessariamente solo per due incontri, il tempo che i "capi" fanno capire agli altri le regole degli incontri.
Poi si possono mischiare tranquillamente.
Adesso analizzo quest'ultimo calendario che mi hai proposto.
"axpgn":
Rielaborando ancora un pochino il primo schema sono giunto a questo prospetto:
1° giorno: $1abc\ \ \ 2def\ \ \ 3ghi\ \ \ 4jkl\ \ \ 5mno$
2° giorno: $3adg\ \ \ 2bkn\ \ \ 4col\ \ \ 5jei\ \ \ 1mhf$
3° giorno: $3ajm\ \ \ 5beh\ \ \ 4cfi\ \ \ 1dko\ \ \ 2gnl$
4° giorno: $4aek\ \ \ 2cgm\ \ \ 3boi\ \ \ 5dhl\ \ \ 1jnf$
5° giorno: $4ahn\ \ \ 5cdj\ \ \ 3bfl\ \ \ 1g\e\o\ \ \ 2mki$
6° giorno: $2afo\ \ \ 4bgj\ \ \ 3ckh\ \ \ 1dni\ \ \ 5mel$
7° giorno: $1ail\ \ \ 4bdm\ \ \ 3cen\ \ \ 5gkf\ \ \ 2jho$
C'è un solo "buco" e solo un caso triplicato (gli altri al massimo duplicati), sempre con la premessa che i "capi" non si incontrino ... difficile fare di più (almeno per me ...
Cordialmente, Alex
Ho verificato ed effettivamente il risultao mi sembra veramente buono! Grazie!!!
Ho aggiunto un ottavo incontro usando questi abbinamenti in modo da coprire anche l'unico buco:
8° giorno: $12eb\ \ \ 34fo\ \ \ 5adn\ \ \ hikm\ \ \ cgjl$
ed il risultato è stato questo:
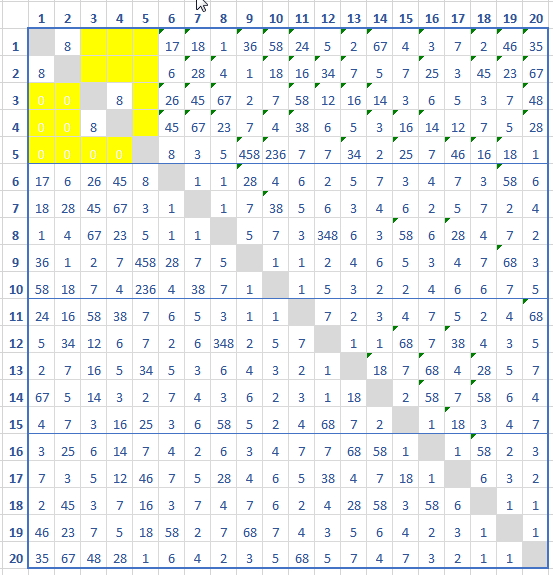
Quando puoi mi interesserebbe conoscere il metodo con cui hai sviluppato il tuo schema,
perchè io continuo ad usare il metodo sgarra-inserta ovvero prova a casaccio...
bye
Pino
Purtroppo nessun metodo ... 
... solo un po' di memoria e di occhio per ritrovare qualcosa di simile e capire che potesse funzionare e poi un bel po' di lavoro per sistemarlo al meglio ... nient'altro ...
Cordialmente, Alex
... solo un po' di memoria e di occhio per ritrovare qualcosa di simile e capire che potesse funzionare e poi un bel po' di lavoro per sistemarlo al meglio ... nient'altro ... Cordialmente, Alex
quindi il famoso metodo sgarra-inserta
Versione alternativa ...
Invece di partire dal "basso" (cioè trovare una soluzione "perfetta" con meno partecipanti per poi ampliarla), ho approcciato il problema "dall'alto" (cioè trovare una soluzione "perfetta" con più partecipanti per poi sfoltirla) e con un po' di ricerche e lavoro ho messo insieme questa:
È riferita ai $21$ partecipanti del problema iniziale e fa sì che tutti incontrino tutti una volta e solo una volta ma ha l'inconveniente che i gruppi non sono omogenei cioè sono formati da tre, quattro o cinque persone ...
Cordialmente, Alex
Invece di partire dal "basso" (cioè trovare una soluzione "perfetta" con meno partecipanti per poi ampliarla), ho approcciato il problema "dall'alto" (cioè trovare una soluzione "perfetta" con più partecipanti per poi sfoltirla) e con un po' di ricerche e lavoro ho messo insieme questa:
È riferita ai $21$ partecipanti del problema iniziale e fa sì che tutti incontrino tutti una volta e solo una volta ma ha l'inconveniente che i gruppi non sono omogenei cioè sono formati da tre, quattro o cinque persone ...
Cordialmente, Alex
Interessante soluzione Alex
Però ancora una volta non ho capito il tuo modo di procedere.
Mi puoi spiegare meglio come hai "sfoltito"?
grazie ancora per il tuo interessamento
Però ancora una volta non ho capito il tuo modo di procedere.
Mi puoi spiegare meglio come hai "sfoltito"?
grazie ancora per il tuo interessamento
Semplice, si vede anche ad "occhio" e scaturisce dalla premessa: ho trovato una soluzione "perfetta" per $25$ persone (suddivise in cinque gruppi da cinque) e poi ho tolto il $22, 23, 24$ e $25$ ...
Cordialmente, Alex
Cordialmente, Alex
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo