Triangolo nel triangolo

[axpgn]

Dato un triangolo acutangolo, qual è il triangolo inscritto in esso dal minor perimetro?
Dimostrazione.

Cordialmente, Alex

[giammaria2]

Mando la mia risposta, anche se la parte finale della dimostrazione mi piace poco.

Il perimetro minore si ottiene congiungendo i piedi delle altezze.
Figura: $ABC$ è il triangolo dato; $DEF$ è quello interno (con D su AB, E su BC, F su CA); $D_1, D_2$ sono i simmetrici di D rispetto ad AC,BC; $M$ è il punto medio di $D_1D_2$.
Dimostrazione: si ha $DF=D_1F$ e $DE=ED_2$, quindi il perimetro è uguale alla spezzata $D_1EFD_2$ ed è minimo quando la spezzata diventa il segmento $D_1D_2$.
Resta da determinare la miglior posizione di D. Notiamo che per le simmetrie si ha $CD_1=CD$ e $CD_2=CD$, quindi il triangolo $CD_1D_2$ è isoscele e $CD_1M$ è la sua metà, rettangolo.
Sempre per le simmetrie, si ha

${(D_1 hatCD=2A hatCD),(D hatCD_2=2DhatCB):}-> D_1 hatCD_2=2(AhatCD+DhatCB)=2 gamma->D_1hatCM=gamma$

Da quanto detto consegue

$D_1D_2=2D_1M=2CD_1 sin gamma=2 CD sin gamma$

che è minimo quando lo è CD, cioè quando D è il piede dell'altezza relativa ad AB.
Ragionando analogamente, si trova che affermazioni simili valgono anche per E,F e quindi vale la mia risposta.

Trovo però poco convincente l'ultima frase scritta (e se ci fossero tre soluzioni distinte?) e per questo aprirò un altro post, che penso di intitolare "Piedi delle altezze", sperando che qualcuno la migliori. Per ora, riesco solo a dimostrare che
$"perimetro minimo"=(2S)/R$
con la solita simbologia (S è l'area di ABC ed R è il raggio del cerchio circoscritto).

[axpgn]

Conosco due dimostrazioni del perché quello individuato da giammaria è il triangolo inscritto di minor perimetro.
Una è impostata come quella di giammaria ma si conclude diversamente ed entrambe fanno uso solo della geometria sintetica.

Cordialmente, Alex

[axpgn]

Ecco la prima (che poi, cronologicamente, sarebbe la seconda ), non fa uso della trigonometria, solo sintetica (la geometria non la dimostrazione )

- triangolo acutangolo $ABC$
- triangolo arbitrario $UVW$ inscritto in $ABC$ con $U$ su $BC$, $V$ su $CA$ e $W$ su $AB$.
- siano $U'$ e $U''$ i simmetrici di $U$ rispetto ad $AC$ e ad $AB$.
- il perimetro del triangolo $UVW$ è pari alla spezzata $U'VWU''$
- tenendo fisso $U$, rimangono fissi pure $U'$ e $U''$, pur spostando $V$ e $W$
- il percorso più breve da $U'$ a $U''$ è la retta quindi la spezzata $U'VWU''$ sarà la più corta quando $V$ e $W$ si troveranno sul segmento $U'U''$
- conseguentemente il segmento $U'U''$ è il minor perimetro possibile per un triangolo inscritto in $ABC$ con un vertice in $U$

Adesso va trovato il punto $U$ che renda "minimo" questo triangolo

- il triangolo $AU'U''$ è isoscele e la lunghezza dei suoi lati obliqui dipendono dalla lunghezza di $AU$
- invece l'angolo $U'AU''$ non dipende dalla posizione di $U$ ma solo dal triangolo $ABC$, quindi la sua ampiezza è costante
- il nostro obiettivo è trovare il minimo $U'U''$
- dato che l'angolo $U'AU''$ non dipende da $U$, tra tutti i triangoli $AU'U''$ quello con la base minore avrà anche i lati minori
- ma i lati sono uguali ad $AU=AU'=AU''$ quindi dobbiamo cercare il segmento $AU$ più corto
- e questo lo avremo quando $AU$ è l'altezza di $ABC$ rispetto a $BC$

Ricapitolando abbiamo dimostrato che il triangolo con il minor perimetro è quello costruito in questo modo con $U$ piede dell'altezza.
Lo stessa costruzione possiamo rifarla sugli altri due lati.
Quindi il triangolo inscritto con il minor perimetro è quello con vertici i piedi delle tre altezze.

Cordialmente, Alex

[axpgn]

Aggiungo una precisazione …

Dalla dimostrazione precedente forse non è chiaro perché il triangolo inscritto costruito in quel modo è unico.
Provo a dettagliare meglio.
Costruiamo il triangolo "minimo" con le "istruzioni" del post precedente.
Abbiamo il triangolo acutangolo $ABC$ in cui inscriviamo il triangolo "minimo" $EFG$ in questo modo:
Sia $E$ il piede dell'altezza da $A$ su $BC$.
Siano $E'$ ed $E''$ i simmetrici di $E$ rispetto ad $AC$ e ad $AB$.
Quindi il segmento $E'E''$ è la lunghezza del perimetro minimo.
I due punti $F$ e $G$ sono le intersezioni di $E'E''$ con $AC$ e $AB$.
Inscriviamo in $ABC$ un qualsiasi triangolo $UVW$ diverso da $EFG$, con $U$ su $BC$, $V$ su $AC$ e $W$ su $AB$.
Per quanto dimostrato precedentemente, se $U$ è diverso da $E$ allora il segmento $U'U''$ sarà più lungo di $E'E''$ e quindi il perimetro di $UVW$ sarà maggiore; se invece $U$ ed $E$ coincidessero allora almeno uno tra $V$ e $W$ non coinciderà con $F$ e con $G$, di conseguenza la spezzata $E'VWE''$ sarà più lunga del segmento $E'E''$ ed anche in questo caso il triangolo $UVW$ avrà un perimetro maggiore di $EFG$.
Quindi esiste un solo triangolo che ha il perimetro minore di tutti quelli inscrivibili.
Ora questa costruzione parte da UN solo piede di altezza ($E$) mentre di $F$ e $G$ non sappiamo niente.
Ma questa costruzione è replicabile su entrambi gli altri due lati ovvero partendo dagli altri due piedi di altezza e siccome il triangolo "minimo" è unico allora non potrà che essere quello che si ottiene collegando i tre piedi della altezze.

Cordialmente, Alex

[axpgn]

Ecco la seconda dimostrazione ...

- triangolo acutangolo $ABC$
- triangolo $EFG$ inscritto in $ABC$ formato unendo i piedi delle tre altezze, con $E$ su $BC$, $F$ su $AC$ e $G$ su $AB$.
- generico triangolo $UVW$ inscritto in $ABC$ con $U$ su $BC$, $V$ su $AC$ e $W$ su $AB$.

*** gli angoli $AFG$ e $CFE$ sono uguali.
[ot]Dimostrazione:
Detto $O$ l'ortocentro di $ABC$, i punti $A, O, F, G$ si trovano tutti sulla circonferenza di diametro $AO$ (perchè $AGO$ e $AFO$ sono triangoli rettangoli), così come i punti $C, O, F, E$ si trovano tutti sulla circonferenza di diametro $CO$.
L'angolo $AFO$ insiste sull'arco $AG$ così come l'angolo $AOG$ perciò essi sono uguali; allo stesso modo accade per gli angoli $CFE$ e $COE$:; ma gli angoli $AOG$ e $COE$ sono opposti al vertice e quindi uguali.
In conclusione $AFG=CFE$.
Lo stesso avviene agli altri due vertici del triangolo $EFG$.[/ot]

Partendo dal triangolo $ABC$, lo ribaltiamo (con tutto il suo contenuto cioè i due triangoli inscritti) lungo il lato $BC$ ed otteniamo il triangolo $CBA'$.
Ripetiamo l'operazione sul lato $CA'$ per ottenere $CA'B'$ e poi ancora lungo $B'A'$ (da cui $A'B'C'$) e di nuovo in $B'C'$, poi in $A''C'$ ed infine lungo $A''B''$ per ottenere il triangolo $A''B''C''$.
Di fatto il triangolo $ABC$ si è spostato in $A''B''C''$ parallelamente a sè stesso senza ruotare (o meglio è ruotato di 360°). Conseguentemente $BC$ è paralello a $B''C''$.
Usando la proprietà *** notiamo che la "seconda posizione" di $EG$ (cioè $EG'$) forma un segmento rettilineo con la prima posizione di $EF$. Allo stesso modo notiamo che un lato del nostro triangolo minimo è sempre allineato con questo segmento.
Ovvero il segmento "diritto" $E''E$ è formato da sei segmenti (due $FG$, due $GE$, due $EF$) cioè il doppio del perimetro del triangolo "minimo" mentre la spezzata $UV'W'U'V''W''U''$ è pari al doppio del perimetro del triangolo $UVW$.
Sappiamo già che i segmenti $UE$ e $U''E''$ sono paralleli, inoltre sono uguali perchè corrispondono agli stessi punti del triangolo $ABC$.
Di conseguenza $E''U''UE$ è un paralellogramma e quindi $E''E=U''U$ cioè $UU''$ è lungo come il perimetro del triangolo "minimo" ma è più corto della spezzata che connette $U$ con $U''$ che è pari al perimetro del triangolo generico $UVW$.
In conclusione il perimetro di $EFG$ è minore di quello di qualsiasi altro triangolo inscritto in $ABC$

Cordialmente, Alex

[Erasmus_First]

Ciao Alex e ciao Giammaria.
Questo quiz (che solo ora vedo qui) è passato in questi giorni in "Rudi Mathematici" (sezione di Coelestis, forum degli astronomi dilettanti).
Io ho trovato una soluzione che mi piace molto e cnsidero originale .
Il percoso su cui procede parte da una banale considerazione di meccanica. Ed è perciò che mi piace e la trovo originale!

Immaginiamo che il dato triangolo di vertici A, B e C sia materiale, rigido ma anche apribile per poterlo concatenare con un altro aggeggio topologicamente pure "anulare", ossia concatenabile col triangolo come due anelli consecutivi di una catena. Allora: apriamo il triangolo acutangolo e con la spezzata ottenuta infiliamo un elastico anulare (come una fettuccia di cameradaria di bicicletta) di circonferenza decisamente inferiore al perimetro del triangolo.
Poi chiudiamo il triangolo. Ora l'elastico è inanellato col triangolo. Allora mettiamo in tensione l'elastico tenendone un estremo mentre l'altro è al centro di un lato in direzione perpendicolare a questo lato ... e poi agganciamo l'estremo che abbiamo in mano all'angolo opposto di questo lato (come una specie di collana!). Più sottop ho messo una figura che spero renda bene l'idea dell'elastico in tensione agganciato ai lati del triangolo rigido. E supponiamo che il triangolo rigido e l'elastico siano lubrificati in modo che l'elastico possa strisciare sui lati del triangolo senza incontrare attrito.. Allora l'elastico si colloca spontaneamente nella posizione di equilibrio stabile, ossia in un minimo di energia elastica e quindi con la minore lunghezza possibile (dipendente esclusivamente dalla forma del triangolo acutangolo rigido)
Allora succede che
a) L'elastico viene a formare un triangolo inscritto in quello acutangolo rigido:
b) La tensione che allunga l'elastico ha lo stesso modulo in ciascuno dei tre lati (dato che non c'è attrito nelle pieghe dell'elastico a ridsso dei lati del triangolo rigido).
c) Due lati del triangolo-elastico hanno la medesima inclinazione sul lato sul quale hanno un estremo in comune perché se così non fosse le componenti della tensione dei due lati nella direzione del lato del triangolo rigido non sarebbero uguali e l'elastico non sarebbe in equilibrio per cui la piega si sposterebbe fino a ripristinare la posizione di uguale inclinazione dei due lati dell'elastico.
Un piccolo esame sugli angoli di uguale inclinazione porta alla conclusione che nella piega dell'elastico a ridosso di un certo lato del triangolo rigido, le inclinazioni su quel latio dei due lati dell'elastico sono uguali all'angolo opposto a quel lato del triangolo rigido. E alla fine a concludere che dei quattro triangolini che son venuti a formarsi tre – quello centrale costituito dall'elastico escluso – sono simili al triangolo rigido.
Allora si possono scrivere proporzioni in numero sufficiente a calcolare le lunghezze di ttutti i 9 segmenti.
Ho disegnato una figura che intende mostrare il triangolo a perimetro minimo costituito da un elastico che si dispone spontaneamente nella posizione giusta. La figura può essere di riferimento per calcolare il perimetro del triangolo


Se a, b e c sono le lunghezze dei lati del triangolo rigid ABC rispettivamente opposti ai verici A, B e C, i coseni degli angoli di vertice rispettivo A, B e C valgono
$cos(α) = (b^2 + c^2 - a^2)/(2bc)$;
$cos(β) = (c^2 + a^2 - b^2)/(2ca)$;
$cos(γ) = (a^2 + b^2 - c^2)/(2ab)$.
Con ciò le lunghezze dei lati del triangolo inscritto a perimetro minimo risultano
$u = a·cos(α)$:
$v = b·cos(β)$;
$w = c·cos(γ)$.
Con i simboli della figura qui sopra, se diciam $r$ il raggio del cerchi inscritto in ABC e diciamo $R$ il raggio del cerchio circoscritto ad ABC tteniamo l'uguaglianza:
$ (u +v + w)/(a + b + c) = r/R$,

________

[axpgn]

@Erasmus_First
Prima di tutto, metti i dollari al posto giusto altrimenti non si capisce il finale …
Poi vedo che i nostri problemini piacciono anche altrove …

Mi pare che la tua idea sia, in un certo qual modo, analoga a quella su cui si basa la seconda soluzione che ho postato … d'altra parte mi sembra che tu ti "limiti" a calcolare il perimetro minimo senza però dire qual è il triangolo inscritto dal perimetro minimo che è la cosa più importante ... IMHO

Che ne pensi invece delle soluzioni che abbiamo scritto?

Cordialmente, Alex

[Erasmus_First]

Ho corretto i "dollari". (editando apposta).

"axpgn":@Erasmus_First
[...] tu ti "limiti" a calcolare il perimetro minimo senza però dire qual è il triangolo inscritto dal perimetro

Non èvero che "mi limito a calcolare il perimetro minimo" ma è vero che non dico quall è il triangolo inscritto con tale perimetro, (cioè non dico dove stanno i suoi vertici sui lati del dato triangolo [acutangolo] .
Ma mi pare che è prroprio questo il bello della mia soluzione!
Trovo infatti le lunghezze dei lati del triangolino ignorando dove stanno i vertici (i quali vanno a posizionarsi "spontaneamente" dove la tensione dell'elasstico viene ad essere la minima possibile
Ma ho altro da ridire a riguardo di questa tua critica (pardon; tuo giusto rilievio] ... e lo metto dentro a "spoiler".

Il fatto è che la versione del quiz passato in "Rudi Mathematici" chiedeva proprio soltanto quanto valesse il perimetro del triangolo a perimetro minimo inscritto in un trìangolo di lati lunghi rispettivamente 17, 25, 26. Naturalmente il quiz meritava una generalizzazione, soprattutto per il fatto che l'idea dell'elastico m'è venuta per prima, per cui la risposta numerica l'ho calcolata come applicazione della suluzione generalizzata (per un triangolo acutangolo di lati di lunghezza [simbolica] a, b e c)
Però ... nel testo che ho messo in spoiler c'è spiegato un po' tyutto, e cioè:
• che i tre triangolini con un vertice in comune col triangolone ABC ono tutti simili a questo;
• che i due angoli di inclinazione di due lati dell'elastico sul lato di ABC nel quale hanno un estremo comune sono uguali all'angolo opposo a quel lato di ABC;
• che in ciascuno dei tre triangolini simili al triangolone il lato costituito dall'elastico è ricavabile dal lato che in ABC è opposto all'angolo in comune moltiplicandolo per il coseno di quell'angolo
• e (in fine) che dalla similitudine di tre triangoli col triangolone si ricavano facilmente TUTTE le lunghezze dei 9 segmenti.
Per esempio, considerando (nella mia figura che ripeto):

che le inclinazione di FE e di FD su AB valgono γ (cioè quanto l'angolo opposto ad AB, quello in C), iccome – come ho detto –
$u = a·cos(α)$ e $v= b·cos(β)$,
viene per forza
FA=$b·cos(α)$ e BF[/Ii= $a·cos(β)$.
Guarda caso, questi valori sono proprio le proiezioni ortogonali dei latt di lunghezza b ed a su quello di lunghezza c,
In altre parole F è il piede delll'altezza di ABC relativa ad AB su AB stesso.
[Analogamente si dica per D ed E].
Insomma: dove stanno i vdertici di DEF non l'ho detto perché pensavo che non fosse richiesto. Ma da quanto si trova col metodo dell'elastico risulta subito (proprio in base a quanto ho detto esplicitamente).
Da notare che, come è indicato nella figura (in cui, come al solito, i simboli x, y e z rappresentano incognite), prima di calcolare le lunghezze u, v e w, bisogna venir a conoscere
x = AF, y = BD e z = CE
che dànno i rapporti di proporzione rispettivamente di AEF, DBF e DEC con ABC.
Insomma: dove stanno i vertici D, E e F non è detto esplicitamente; ma tra le righe è detto quanto valgono i 6 segmenti individuati suui lati di ABC dai vertici di DEF.

________

[axpgn]

@Erasmus
Avrai anche corretto "i dollari" ma io continuo a vedere "sballata" la parte finale del tuo post (precedente).
Boh!

"Erasmus_First":… ma è vero che non dico quall è il triangolo inscritto con tale perimetro, ...

Vedi che ho ragione io?

Oh, non discuto la tua bella soluzione (inciso: anche la seconda soluzione che ho postato parte da una premessa simile e "fisica" anch'essa ovvero la "riflessione ottica") ed è vero che ho chiesto la dimostrazione ma la prima richiesta (esplicita) riguardava quale triangolo ha quella caratteristica, al fine di stabilire un teorema generale: Il triangolo dal minor perimetro inscritto in un triangolo acutangolo è quello formato unendo i piedi delle tre altezze (altro inciso: nel testo originale dice "pedal triangle" così ho imparato una nuova parola che non conoscevo )
A titolo di curiosità aggiungo che la seconda soluzione che ho postato è dovuta a H.A.Schwarz (quello della disuguaglianza) mentre la prima ad un suo allievo, L.Fejér

Cordialmente, Alex

[Erasmus_First]

Ho corretto i "dollari". (editando apposta).

"axpgn":@Erasmus_First
[...] tu ti "limiti" a calcolare il perimetro minimo senza però dire qual è il triangolo inscritto dal perimetro

Non è vero che "mi limito a calcolare il perimetro minimo" ma è vero che non dico quall è il triangolo inscritto con tale perimetro, (cioè non dico dove stanno i suoi vertici sui lati del dato triangolo [acutangolo] .
Ma mi pare che è prroprio questo il bello della mia soluzione!
Trovo infatti le lunghezze dei lati del triangolino ignorando dove stanno i vertici (i quali vanno a posizionarsi "spontaneamente" dove la tensione dell'elasstico viene ad essere la minima possibile
Ma ho altro da ridire a riguardo di questa tua critica (pardon; tuo giusto rilievio] ... e lo metto dentro a "spoiler".

Il fatto è che la versione del quiz passato in "Rudi Mathematici" chiedeva proprio soltanto quanto valesse il perimetro del triangolo a perimetro minimo inscritto in un trìangolo di lati lunghi rispettivamente 17, 25, 26. Naturalmente il quiz meritava una generalizzazione, soprattutto per il fatto che l'idea dell'elastico m'è venuta per prima, per cui la risposta numerica l'ho calcolata come applicazione della suluzione generalizzata (per un triangolo acutangolo di lati di lunghezza [simbolica] a, b e c)
Però ... nel testo che ho messo in spoiler c'è spiegato un po' tutto, e cioè:
• che i tre triangolini con un vertice in comune col triangolone ABC ono tutti simili a questo;
• che i due angoli di inclinazione di due lati dell'elastico sul lato di ABC nel quale hanno un estremo comune sono uguali all'angolo opposo a quel lato di ABC;
• che in ciascuno dei tre triangolini simili al triangolone il lato costituito dall'elastico è ricavabile dal lato che in ABC è opposto all'angolo in comune moltiplicandolo per il coseno di quell'angolo
• e (in fine) che dalla similitudine di tre triangoli col triangolone si ricavano facilmente TUTTE le lunghezze dei 9 segmenti.
Per esempio, considerando (nella mia figura che ripeto):

che le inclinazione di FE e di FD su AB valgono γ (cioè quanto l'angolo opposto ad AB, quello in C), iccome – come ho detto –
$u = a·cos(α)$ e $v= b·cos(β)$,
viene per forza
FA=$b·cos(α)$ e BF[/Ii= $a·cos(β)$.
Guarda caso, questi valori sono proprio le proiezioni ortogonali dei latt di lunghezza b ed a su quello di lunghezza c,
In altre parole F è il piede delll'altezza di ABC relativa ad AB su AB stesso.
[Analogamente si dica per D ed E].
Insomma: dove stanno i vdertici di DEF non l'ho detto perché pensavo che non fosse richiesto. Ma da quanto si trova col metodo dell'elastico risulta subito (proprio in base a quanto ho detto esplicitamente).
Da notare che, come è indicato nella figura (in cui, come al solito, i simboli x, y e z rappresentano incognite), prima di calcolare le lunghezze u, v e w, bisogna venir a conoscere
x = AF, y = BD e z = CE
che dànno i rapporti di proporzione rispettivamente di AEF, DBF e DEC con ABC.
Insomma: dove stanno i vertici D, E e F non è detto esplicitamente; ma tra le righe è detto quanto valgono i 6 segmenti individuati suui lati di ABC fdai vertici di DEF.

________

[axpgn]

Scusa Erasmus ma hai postato di nuovo lo stesso messaggio ? Oppure c'è qualcosa di nuovo che non ho notato?

[Erasmus_First]

"axpgn":Erasmus [...] hai postato di nuovo lo stesso messaggio ? ?

Sì. Me ne accorgo solo adesso (essendo tornato per dire ora qualcosa di nuovo).
Il fatto è che qui il mio computer oppure Internet o tutt'e due ogni tanto hanno delle malfunzioni (di cui mi accorgo a fatti già avvenuti ... che mi restano incompresi ed incomprensibili).
Nel tuo messaggio successivo al mio primo intervento mi chiedevi un parere sulle soluzioni postate da te. Beh: il parere non l'avevo perché dopo aver iniziato a leggiuchiarle mi sono perso in altri pensieri ... e ho lasciato perdere,
E ancora non ho alcuna intenzione di andare a leggerle (e decifrarle ... perché non è detto che riesca a seguirne il ragionamento con la semplice lettura).
Nel tuo messaggio successivo al mio secondo intervento, tu mi riveli che una delle due dimostrazioni postate da te è di Schwarz (quello della disuguaglianza di Cauchy-Schwarz) . Ehh ... non mi metto ,certo io, umile dilettante "amatoriale", a disquisire con giganti della matematica!
Allora: non conoscendo la proprietà di questo triangolo e tantomeno che ha scoprirla sono stati i giganti matematici dell'800, mi compiaccio di averla trovata autonomamente e, soprattutto, con una banale applicazione di meccanica razionale!
––––––––––
Quello di nuovo che volevo dire è qualcosa che ho imparato risolvendo questo quiz (e che in sé non ha nulla a che fare con il perimetro). Qualcosa a cui non avevo mai pensato (benché sia stato insegnante di matematica in Licei, in istituti tecnici e – seppur per poco tempo – anche in altri tipi di scuola).
Permettimi, Alex, una introduzione a quello che sarà il clou di questo mio ulteriore intervento .
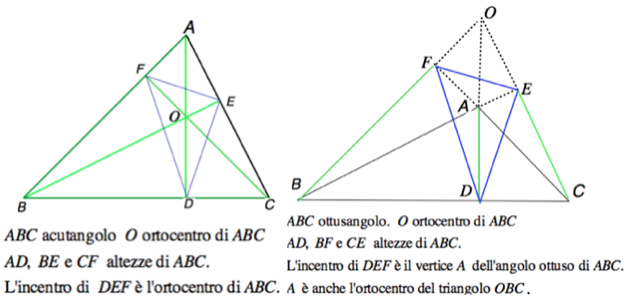
Al ginnasio (mi pare in VIª, corrispondente alla 1ª liceo scientifico, ma forse era in Vª ginnasio), prima si dimostrava che gli assi di un triangolo passavano tutti tre per uno stesso punto equidistante dai vertici (e detto "circocentro"). Poi si dimostrava che anche le tre rette delle altezze passavano per uno stesso punto, (detto "ortocentro"); e questa proprietà si ricavava mostrando che le rette delle altezze erano gli assi di un altro triangolo ottenuto tracciando per ciascun vertice del primo la parallela al lato opposto. Riassumendo: l'ortocentro c'è perché è lo stesso circocentro d'un altro triangolo. Poi si dimostrava indipendentemente da tutto ciò che anche le bisettrici degli angoli interni d'un riangolo passavano per uno stesso punto (equidistante dai lati e detto "incentro").
1) Ora, però, veniamo a scoprire che l'ortocentro di un triangolo ABC acutangolo è anche incentro del triangolino che ha per vertici i piedi delle altezze di ABC sui lati AB, BC e CA di ABC.
Sia O l'ortocentro di ABC.
2) Se ABC è ottusangolo in C, I piedi delle altezze relative ad AC e a BC cascano fuori del triangolo, come pure il suo ortocentro O. Allora, però, è acutangolo il triangolo ABO e il suo ortocentro è C.
I piedi delle altezze relative al nuovo triangolo ABO sono gli stessi piedi delle altezze di ABC sulle rispettive rette AB, BC e CA e sono i vertici di un triangolo il cui incentro è C.
3) Se ABC è acutangolo ed O è il suo ortocentro, allora il triangolo ABO è ottusangolo in O e il suo ortocentro è C

Insomma: Detto O l'ortoocentro di ABC – che se ottusangolo supponiamo esserlo in C – c'è una specie di dualità tra i triangili ABC e ABO.
• Se uno dei due triangoli ABC e ABO è acutangolo l'altro è ottusangolo.
Siano poi D su BC, E su CA ed F su AB i piedi delle altezze di ABC sui suoi lati (o sui prolungamenti dei suoi lati).
Allora D, E ed F sono pure i piedi delle altezze di ABO sui rispettivi lati (o prolungamenti).
• Due altezze di ABC sono due lati di ABO e due altezze di ABO sono lati di ABC
• L'incentro di DEF è l'ortocentro del triangolo acutangolo e vertice dell'angolo ottuso del triangolo ottusangolo.
________



P.S. (Lunedì 11/11/2019 ore21:42)
Edito per aggiungere questa immagine come illustrazione dell'regomento del mio intervento

[axpgn]

Bravo Erasmus

[Erasmus_First]

Là in "Rudi Mathematici", tal nino280 ( assiduo frequentatore di quella sezione di Coelestis ed appassionato sfruttatore di "Geogebra") ha postato, tra l'altro, questa figura:

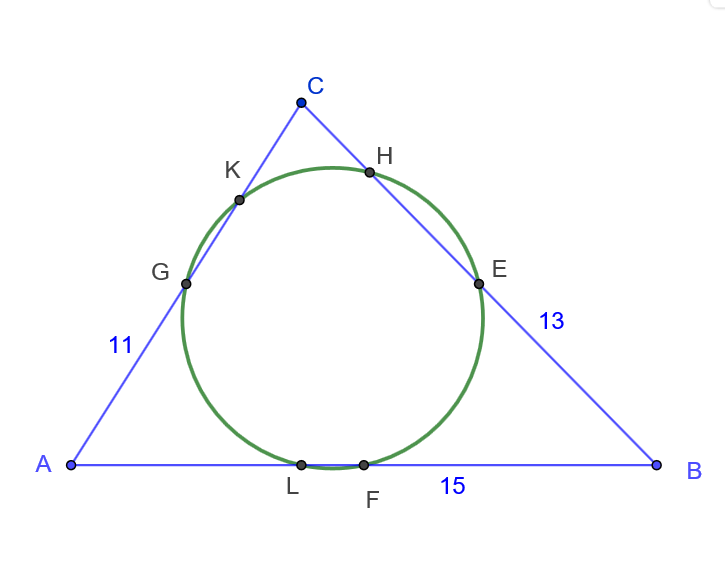
che rappresenta un triangolo ABC e la circonferenza [circolare] che passa per i punti medi dei lati di ABC (che sono E, F e G)
Rispetto ad un triangolo, il cerchio circoscritto al triangolo che ha per vertici i punti medi dei lati si chiama – ma io l'ho impartato solo ieri! – "Cerchio di Feuerbach" perché il matematico tedesco Karl Feuerbach ha scoperto che questo cerchio è pure circoscritto al triangolo che ha per vertcici i piedi delle altezze del dato triangolo sui suoi lati (o sui loro prolungamenti) – H, K ed L in figura –).
Insomma: Il Teorema di Feuerbach afferma che, dato un triangolo ABC, il cercchio circoscitto al triangolo che ha per vertici i punti medi di un dato triangolo è anche circoscritto al triangolo che ha per vertici i piedi delle altezze del dato triangolo sui suoi lati, (quello di cui abbiamo parlato fino ad ora in questo thread ).
Stamattina, con un po' di pazienza ho dimostrato autonomamente il teorema di Feuerbach.
Sono partito dal chiamare K il punto del piano del triangolo ABC equidistante dai piedi delle altezze (piedi che io ho chimato U su BC, V su CA e W su AB, in sintonia con l'aver detto
$u = a·cos(α)$; $v = b·cos(β$; $w = c·cos(γ)$;
i lati del triangolo a perimetro minimo tra quelli inscritti in ABC acutangolo più prossimi rispettivamente ad A, B e C) e dimostrando che K dista da U, V e W la metà del raggio del cerchio circoscritto ad ABC (dato che così vale il raggio del cerchio circoscritto al triangolo che ha per vertici i punti medi dei lati di ABC).

Alex (e qualunque altro eventuale lettore): un bel quiz sarebbe
"Dare una dimostrazione del Tteorema di Feuerbach"
senza andar a scopiazzare in rete!
________

[axpgn]

C'è un problema: il cerchio di Feuerbach lo conoscevo già anzi lo conoscevo (ed è maggiormente conosciuto) come "cerchio dei nove punti" (dove hai lasciato gli altri tre? )
Ha molti altri nomi tra i quali anche "cerchio di Eulero" e secondo Wikipedia passa anche per altri nove punti "rimarchevoli".
E dato che ti appassiona ti dico che anche il centro di questo cerchio ha un nome "proprio" e possiede una caratteristica: quale?

Ciao, Alex

[Erasmus_First]

@ axpgn/Alex
I tre punti oltre ai 6 che ho detto non li ho persi per strada ... solo che siccome nino280 ha nominato quel cerchio come "Cerchio di Feuerbach" mi pareva più giusto ignorarli, mettermi cioè al livello storico di Karl Feuebach.
––––––––––
Il "cerchio di Feuerbach" è stato chiamato così non da Feuerbach ma successivamente in suo onore.
Tempo dopo –ma non so quanto – qualcun altro ha scoperto che questo cerchio passa anche per i punti medi dei tre segmenti di estremi un vertice del triangolo e l'ortocentro.
Dopo tale scoperta è stato nominato anche "cerchio dei 9 punti".
Ho leggiucchiato anch'io l'articolo di Wikipedia cui ti riferisci ... trovando quell'articolo molto superficiale.

Il fatto che tu conoscessi già questo cerchio non equivale all'escluso dal dare qui una dimostrazione del "Teorema di Feuerbach".
[Per paragone: Io so bene che non esiste una formula risolutiva generale per le equazioni algebriche di grado maggiore di 4; e so anche che il teorema che dimostra ciò è stato dimostrato autonomamente da Ruffini, da Abel e da Galois (indipendentemente uno dall'altro). Ma non sarei in grado darne a mia volta una dimostrazione].

Ciao Alex.
Ciao a tutti
________

[axpgn]

Ok, vediamo di dimostrare il "tuo" teorema di Feuerbach (dato che il "Teorema di Feuerbach" è un altro )

Faccio riferimento al tuo disegno: $ABC$ è il triangolo, $E, F, G$ i punti medi e $H, K, L$ i piedi delle tre altezze.

Il quadrilatero $EFLG$ è un trapezio; il segmento $EG$, collegando due punti medi, è parallelo ad $AB$ quindi a $FL$.
È pure isoscele; il segmento $EF$, collegando i punti medi, è la metà di $AC$; d'altra parte $GL$ è la mediana relativa all'ipotenusa del triangolo rettangolo $ACL$ quindi anch'essa è la metà di $AC$.
Di conseguenza il trapezio isoscele $EFLG$ è ciclico ovvero inscrivibile in un cerchio ovvero i quattro punti $E, F, L, G$ stanno sulla stessa circonferenza; lo stesso vale per gli altri due lati.
Tutti i sei punti si trovano sulla stessa circonferenza.

Per gli altri tre … consideriamo il triangolo $ABO$ dove $O$ è l'ortocentro di $ABC$.
I piedi dell'altezze di questo triangolo sono gli stessi di $ABC$ quindi il cerchio che passa per $H, K, L$ passerà anche per i punti medi dei lati di $ABO$ e quindi …

Cordialmente, Alex

[Erasmus_First]

"axpgn":[...] ([...] il "Teorema di Feuerbach" è un altro )

Dico una frase non certo originale: «Non si finisce mai di imparare!»
[Leggo ora, in Wikipedia, ché si intende per "Teorema di Feuerbach"]

"axpgn":Ok, vediamo di dimostrare il "tuo" teorema di Feuerbach [...]

Bravo Alex!

Bravo Alex perché la tua dimostrazione non è "metrica" bensì proprio "euclidea".
Io una tale dimostrazione l'ho cercata ... senza trovarla.
Allora ho fatto ricorso ad una dimostrazione "metrica" .
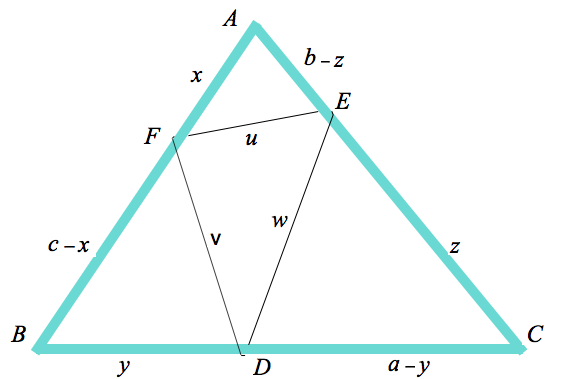
Rimetto la figura di riferimento:

Il triangolo inscritto in ABC a perimetro minimo è HKL. e le lunghezze dei suoi lati sono:
KL = $u = a·cos(α)$: LH = $v = b·cos(β)$; HK = $w = c·cos(γ)$.
1) Per prima cosa ho osservato che il raggio  del cerchio circoscritto al triangolo di lati
$u = a·cos(α)$: $v = b·cos(β)$; $w = c·cos(γ)$
– diciamolo $R$ – vale
$R = u/(2·sin(π-2α)) = v/(2·sin(π-2β)) = w/(2·sin(π-2γ)) =$
$= 1/2·a/(2·sin(α)) = 1/2·b/(2·sin(β))) = 1/2·a/(2·sin(γ))$
ossia quanto quello del cerchio circoscritto al triangolo che ha per vertici i punti medi dei lati di ABC.
2) Poi, (senpre con riferimento alla figura qui sopra alla quale anche tu hai fatto riferimento), detto P il centro di questo cerchio per i piedi H, K ed L delle altezze di ABC sui suoi lati, ho calcolato l'angolo AKP, il suo coseno e quindi la posizione su AC della proiezione ortogonale di P su AC ... trovando che essa è il punto medio del segmento GK (e quindi che GKP è isoscele su GK, ossia che P dista ugualmente da G e da K).
[Idem si può fare sugli altri due lati di ABC).

Riconosco che la tua dimostrazione è molto più elegante della mia ... soprattutto ha il pregio di non essere "metrica" ma essere davvero "euclidea".
________