Strana sucessione, Quand'è che converge?

[Erasmus_First]

Sia [size=120]k[/size] reale e positivo.
Si consideri la successione
{[size=120]a[/size][size=85]n[/size]} = [size=120]a[/size][size=85]0[/size], [size=120]a[/size][size=85]1[/size], [size=120]a[/size][size=85]2[/size], [size=120]a[/size][size=85]3[/size], ...
drfinita ricorrentemente come segue:
[size=120]a[/size][size=85]0[/size] = [size=120]k[/size]; [size=120]∀[/size]n [size=120]∈[/size] [size=120]N[/size] [size=120]a[/size][size=85]n+1[/size] = [size=120]k[/size]^([size=120]a[/size][size=85]n[/size]).
Per quali [size=100]k[/size] converge tale successione?

[axpgn]

Bentornato Erasmus

[axpgn]

Mi pare di poter affermare che $k=1$ funzioni, poi vedremo ... forse ...

[axpgn]

Da esperimenti fatti ( ) converge per $k<=2$
Comunque questo problema si ricollega a quello classico della "torre" di $2$, che si trova anche qui da qualche parte

[hydro1]

E' un problema la cui soluzione è facile da pensare graficamente. Ovviamente è interessante solo per $k>1$, perchè altrimenti è chiaro che la successione converga. Chiama $f_k(x)=k^x$. Ti stai chiedendo quando l'iterata $n$-esima di $k$ sotto questa funzione converge; se questo accade ed il limite è \(\ell\), allora \(f_k(\ell)=\ell\), per continuità di $f_k$. Quindi necessariamente l'equazione $k^x=x$ deve avere almeno una soluzione. Ora, com'è fatta la fuzione $g_k(x)=f_k(x)-x$? La derivata ha un solo zero, che è $x_0=-\log_k(\log k)$. Siccome $g_k(0)=1$ e $g_k(x)\to +\infty$ quando $x\to \infty$, ciò significa che (per ogni $k$ fissato) $g_k$ decresce fino a $x_0$ e poi cresce. Ora, quando $g_k(x_0)>0$ l'equazione $f_k(x)=x$ non ha radici, quindi la successione diverge (dal momento che è monotona crescente). Che succede quando $g_k(x_0)\le 0$? Intanto se uno disegna il grafico della funzione (della variabile $k$) $y=g_k(x_0)$, si accorge che ha un unico zero, chiamiamolo $k_0$. Si vede anche che è $>1$. Quando $10$ si deve necessariamente avere $11$ si ha $a^a>a$ la successione $a_n$ è necessariamente monotona crescente, e dall'altra parte siccome $k

Cita

Segnala

[hydro1]

Tra l'altro effettivamente si può proprio risolvere l'equazione $g_k(x_0)=0$ e si trova che $k_0=e^{1/e}$.

[e3353cdc139f9576d1418ef5ef3cff2aac614a86]

"hydro":Ovviamente è interessante solo per $k>1$, perchè altrimenti è chiaro che la successione converga.

Sembra di no, se $k$ è troppo piccolo la successione non converge. Cercando su internet "infinite tower power" si trovano tante cose.

[hydro1]

"Martino":[quote="hydro"]Ovviamente è interessante solo per $ k>1 $, perchè altrimenti è chiaro che la successione converga.

Sembra di no, se $ k $ è troppo piccolo la successione non converge. Cercando su internet "infinite tower power" si trovano tante cose.

[/quote]

Aaaah hai ragione, che sciocco. Quel che ho detto sopra allora è valido solo per $k\ge 1$.

[hydro1]

Comunque anche per $k<1$ l'idea è la stessa: quando il punto fisso di $k^x$ è attrattivo, cosa che avviene per $k>e^{-e}$, localmente la mappa $k^x$ è una contrazione, quindi se si dimostra che $k$ è sufficientemente vicino al punto fisso, la successione converge. Viceversa per $k

Cita

Segnala

[otta96]

L'avevo un po' studiata anch'io anni fa, pare che sia pure l'inversa di $x^(1/x)$ dove è definita.

[Erasmus_First]

Sia x il limite della successione convergente per un certo k > 0.
Allora, al tendere all'infinito dell'indice della successione deve essere x = k^x, ossia:
k = x^1/x).

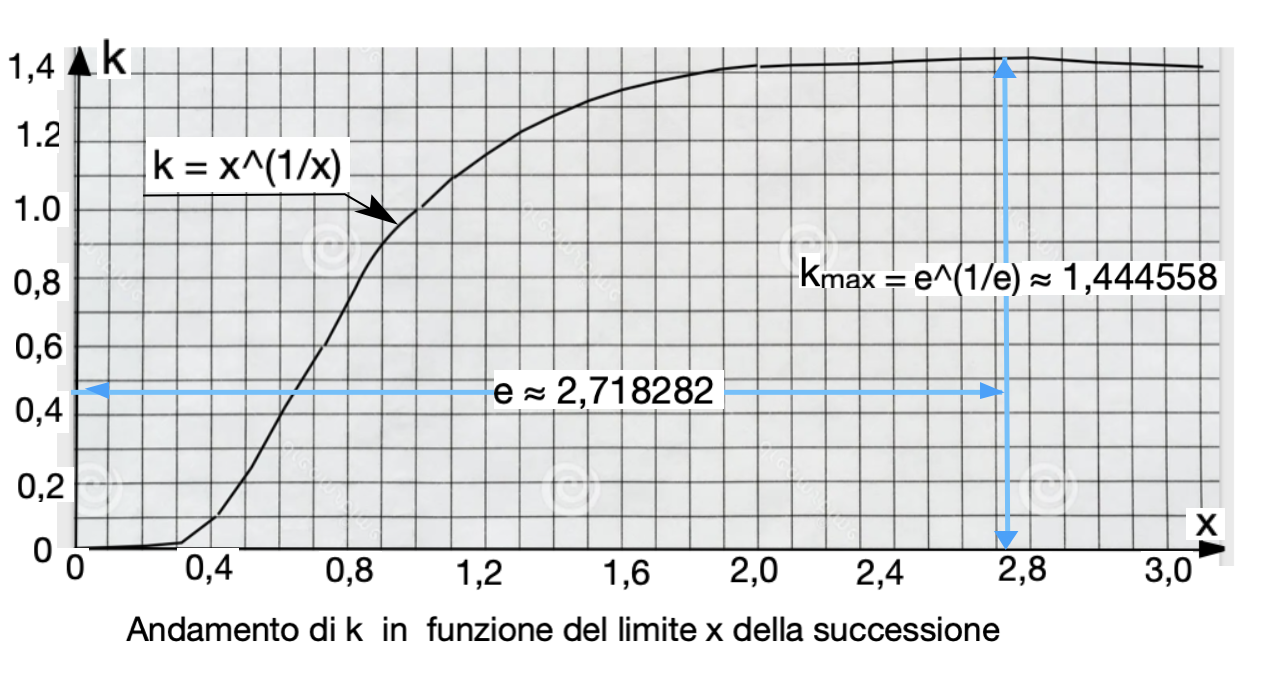
Il massimo do k in funzione di x è_
Kmax = e^(1/e).
Pertanto la risposta al quiz è:
0 < k ≤ e^(1/e).

[Quinzio]

Per valori piccoli di $k$ la successione oscilla su due valori.
Mi sembra che lo faccia per $k < 0.066$ circa, determinato graficamente.

[otta96]

A memoria era una potenza con tante "$e$", mi sembra $e^-e$, e guardando con Wolframalpha sembrerebbe tornare con quello che dice Quinzio, anche se mi ricordo che non ero riuscito a dimostrarla questa cosa.
EDIT: ah ma l'aveva scritto già hydro, eh vabbè, non me n'ero accorto.

[e3353cdc139f9576d1418ef5ef3cff2aac614a86]

Quindi abbiamo capito che per $k$ abbastanza piccolo la successione arriva ad oscillare tra due valori distinti. Qualcuno sa quali siano questi due valori? (In funzione di $k$ ovviamente).

[hydro1]

"Martino":Quindi abbiamo capito che per $k$ abbastanza piccolo la successione arriva ad oscillare tra due valori distinti. Qualcuno sa quali siano questi due valori? (In funzione di $k$ ovviamente).

Si verifica facilmente che per $k

Cita

Segnala

[e3353cdc139f9576d1418ef5ef3cff2aac614a86]

Sì credo anch'io, ma $x_0$ si può calcolare? (In funzione di $k$).

[Quinzio]

"Martino":Sì credo anch'io, ma $x_0$ si può calcolare? (In funzione di $k$).

Mi vien da dire di no.
E' la soluzione di $x = k^{k^x}$ o se si preferisce, di $root{x}x = k^k$